Четырехугольник и его элементы

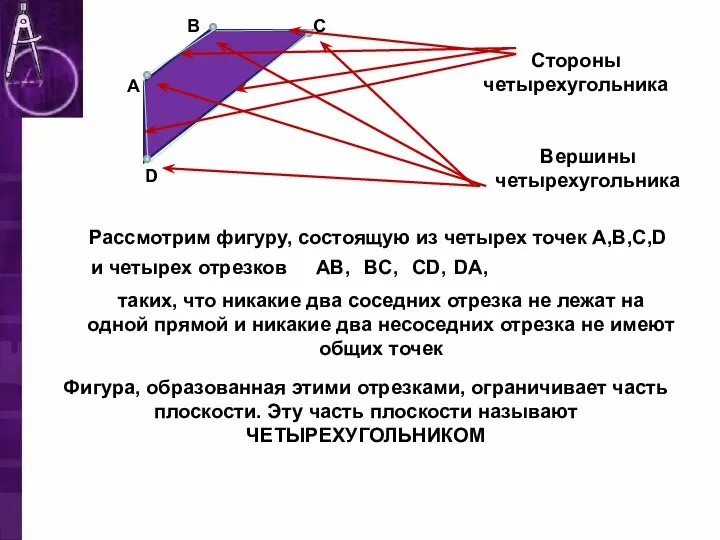
Рассмотрим фигуру, состоящую из четырех точек A,B,C,D
A
B
C
D
и четырех отрезков
AB,
BC,
CD,
DA,
таких, что никакие два соседних отрезка не лежат на одной прямой и никакие два несоседних отрезка не имеют общих точек
Фигура, образованная этими отрезками, ограничивает часть плоскости. Эту часть плоскости называют ЧЕТЫРЕХУГОЛЬНИКОМ
Вершины четырехугольника
Стороны четырехугольника

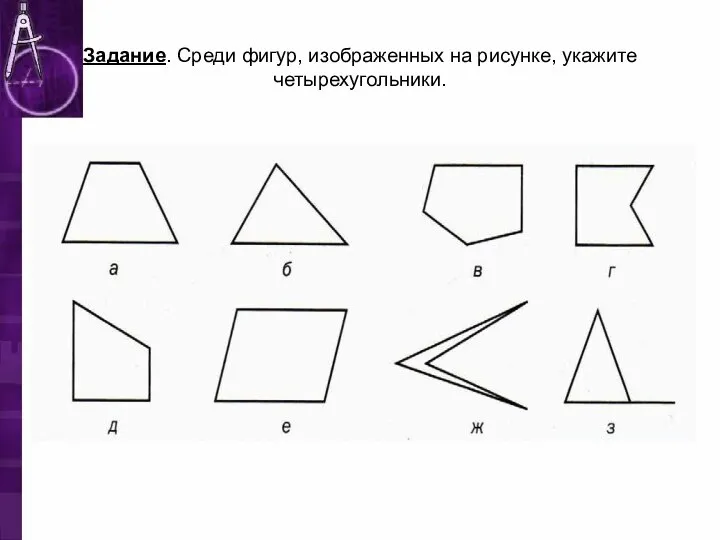
Задание. Среди фигур, изображенных на рисунке, укажите четырехугольники.

Стороны четырехугольника, являющиеся соседними отрезками, называются соседними сторонами четырехугольника
Вершины четырехугольника, являющиеся концами одной стороны, называют соседними вершинами четырехугольника
Стороны четырехугольника, не являющиеся соседними, называют противолежащими сторонами четырехугольника
Несоседние вершины четырехугольника, называют противолежащими вершинами четырехугольника
Отрезок, соединяющий противолежащие вершины четырехугольника, называют диагональю четырехугольника

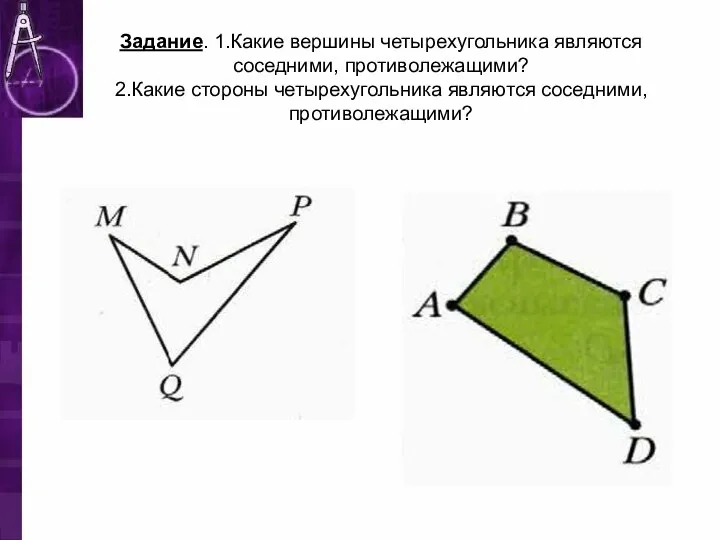
Задание. 1.Какие вершины четырехугольника являются соседними, противолежащими?
2.Какие стороны четырехугольника являются соседними, противолежащими?

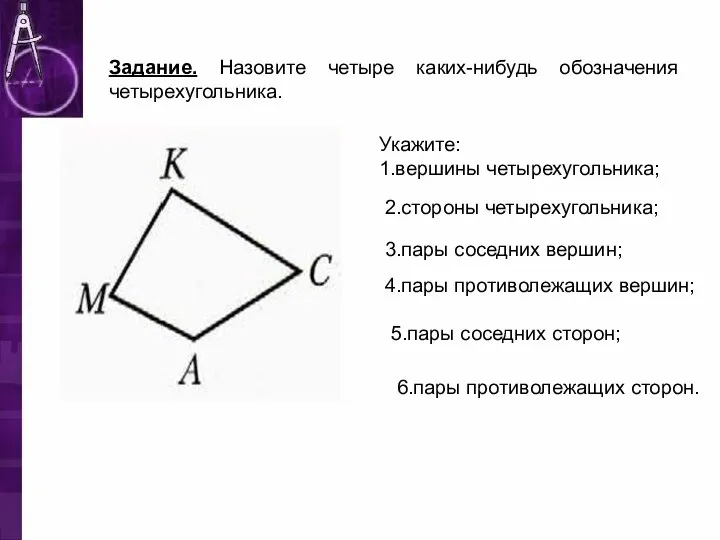
Укажите:
1.вершины четырехугольника;
Задание. Назовите четыре каких-нибудь обозначения четырехугольника.
2.стороны четырехугольника;
3.пары соседних вершин;
4.пары противолежащих вершин;
5.пары соседних сторон;
6.пары противолежащих сторон.

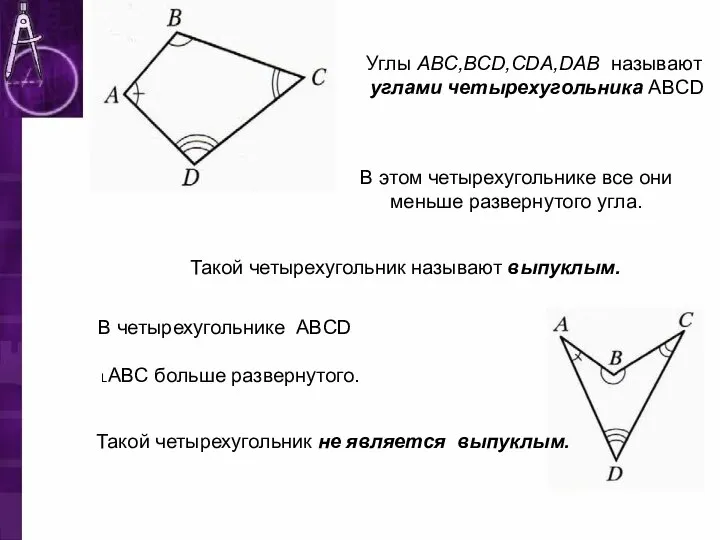
Углы ABC,BCD,CDA,DAB называют
углами четырехугольника ABCD
В этом четырехугольнике все они меньше развернутого угла.
Такой четырехугольник называют выпуклым.
В четырехугольнике ABCD
˪ABC больше развернутого.
Такой четырехугольник не является выпуклым.

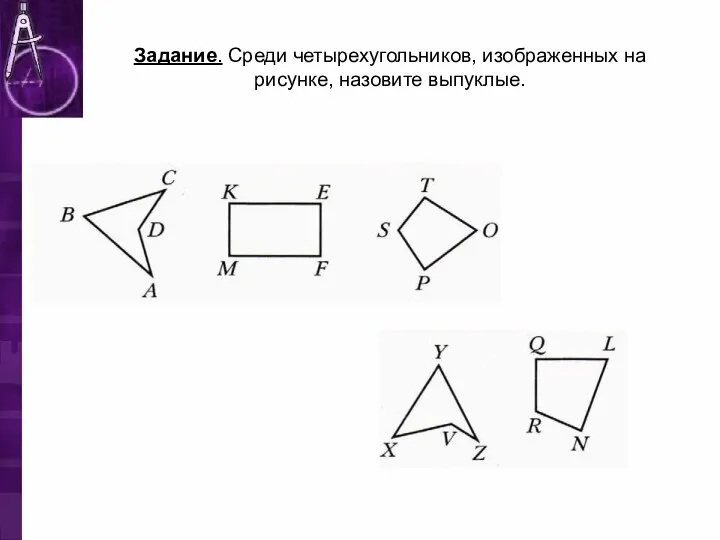
Задание. Среди четырехугольников, изображенных на рисунке, назовите выпуклые.

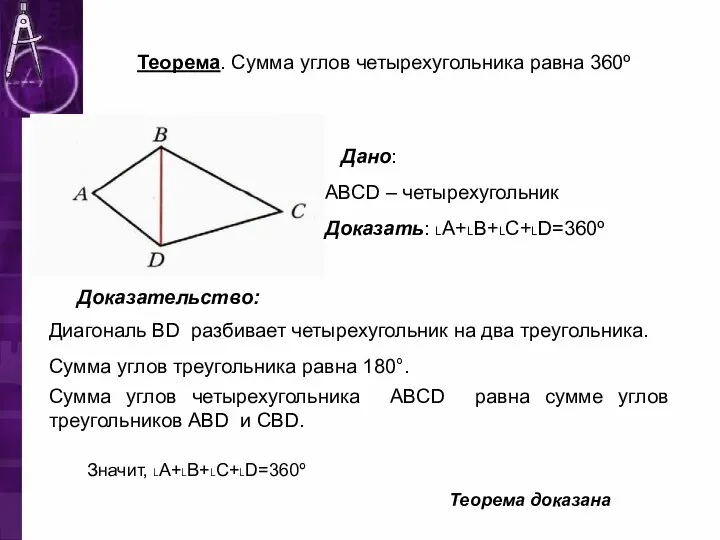
Теорема. Сумма углов четырехугольника равна 360º
Дано:
АBCD – четырехугольник
Доказать: ˪А+˪В+˪С+˪D=360º
Доказательство:
Диагональ BD разбивает четырехугольник на два треугольника.
Сумма углов треугольника равна 180°.
Сумма углов четырехугольника ABCD равна сумме углов треугольников ABD и CBD.
Значит, ˪А+˪В+˪С+˪D=360º
Теорема доказана

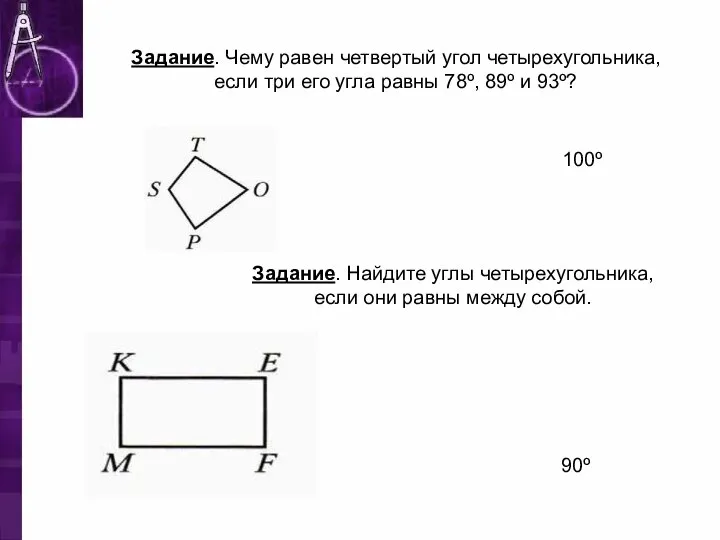
Задание. Чему равен четвертый угол четырехугольника, если три его угла равны 78º, 89º и 93º?
100º
Задание. Найдите углы четырехугольника, если они равны между собой.
90º

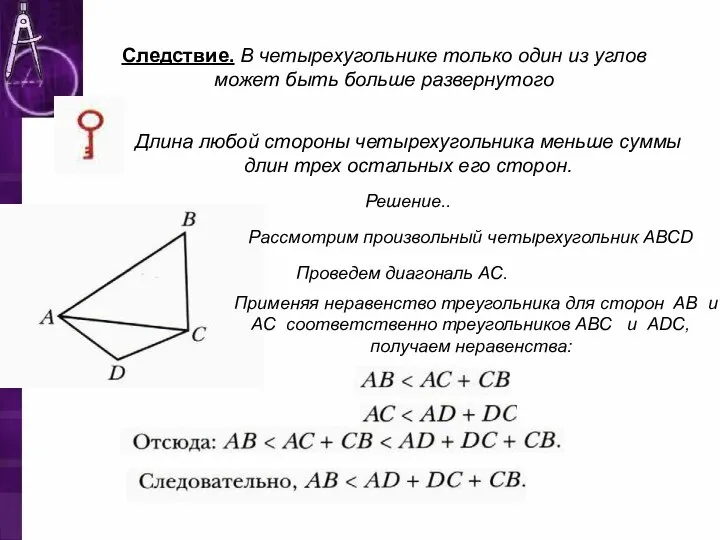
Следствие. В четырехугольнике только один из углов может быть больше развернутого
Длина любой стороны четырехугольника меньше суммы длин трех остальных его сторон.
Рассмотрим произвольный четырехугольник ABCD
Проведем диагональ AC.
Применяя неравенство треугольника для сторон AB и AC соответственно треугольников ABC и ADC, получаем неравенства:
Решение..