Содержание
- 2. Уравнение поверхности в пространстве Уравнение с тремя переменными задает в пространстве некоторую поверхность , если координаты
- 3. Составим уравнение плоскости, проходящей через точку и вектором нормали Уравнение плоскости (общее) Вектор нормали к плоскости
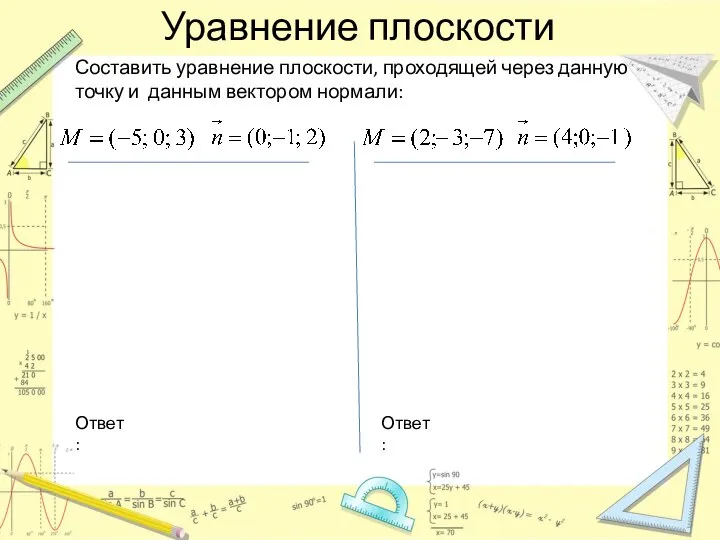
- 4. Уравнение плоскости Составить уравнение плоскости, проходящей через данную точку и данным вектором нормали: Ответ: Ответ:
- 5. Уравнение плоскости Составить уравнение плоскости, проходящей через данную точку и данным вектором нормали: Ответ: Ответ:
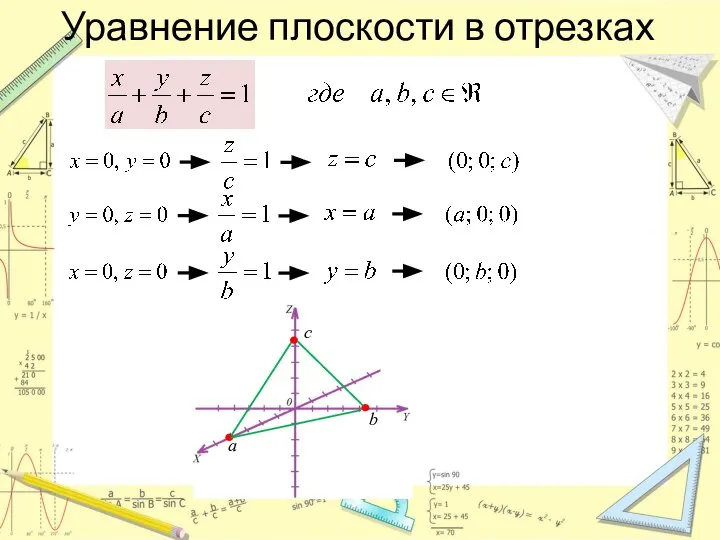
- 6. Уравнение плоскости в отрезках c a b
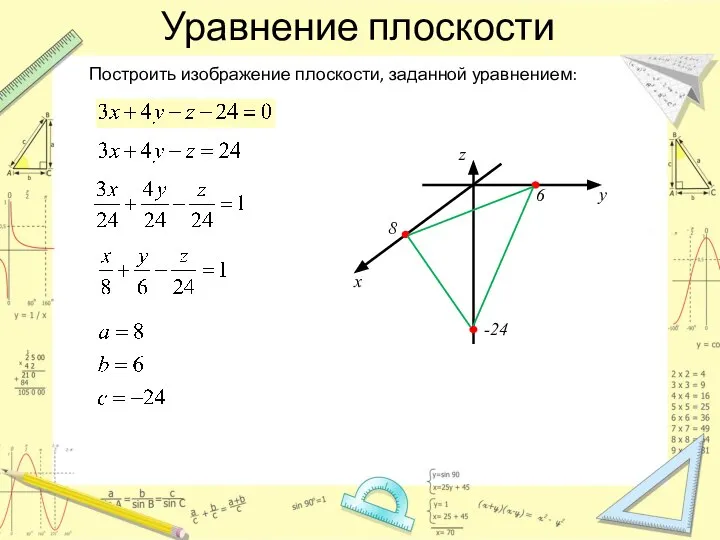
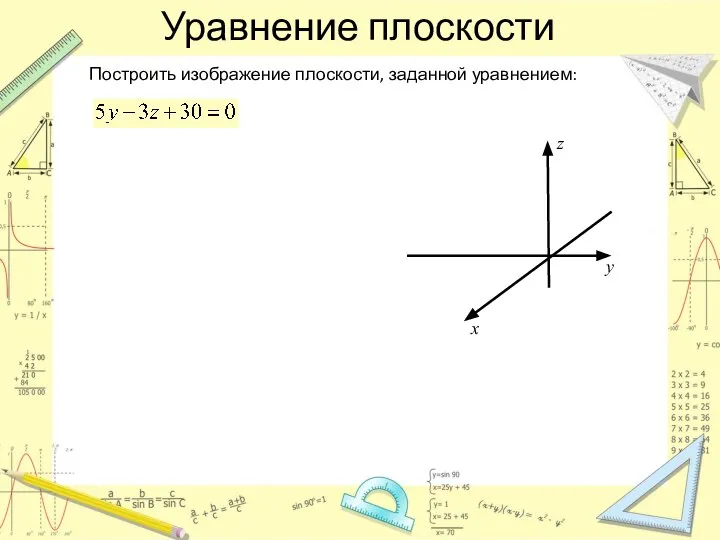
- 7. Уравнение плоскости Построить изображение плоскости, заданной уравнением: z y x 8 6 -24
- 8. Уравнение плоскости Построить изображение плоскости, заданной уравнением: z y x -3/2 3/5 1/3
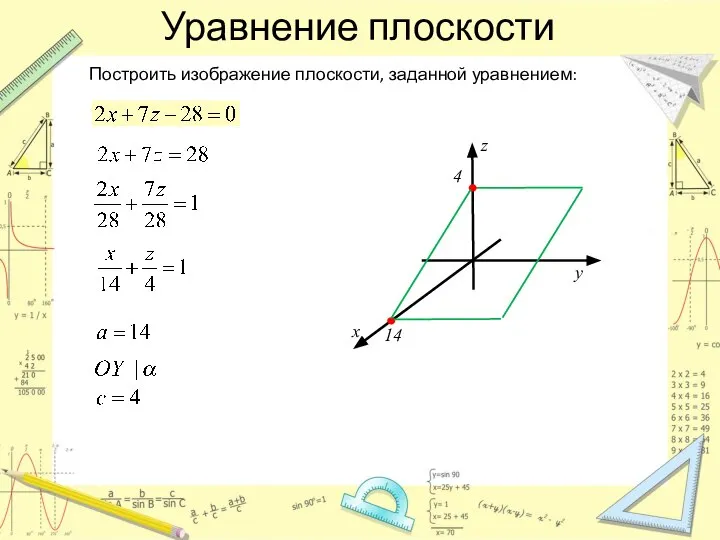
- 9. Уравнение плоскости Построить изображение плоскости, заданной уравнением: z y x 14 4
- 10. Уравнение плоскости Построить изображение плоскости, заданной уравнением: z y x
- 12. Скачать презентацию




 Презентация на тему Сечения многогранников
Презентация на тему Сечения многогранников  Заколдованные цифры
Заколдованные цифры Объёмные и плоские геометрические фигуры
Объёмные и плоские геометрические фигуры Случаи сложения вида +7
Случаи сложения вида +7 Матрица размера m x n
Матрица размера m x n Применение производной. Учебно-тренировочные материалы для подготовки к ЕГЭ
Применение производной. Учебно-тренировочные материалы для подготовки к ЕГЭ Собирательные числительные
Собирательные числительные Решение задач с помощью составления систем уравнений
Решение задач с помощью составления систем уравнений Параллелограмм
Параллелограмм Системы линейных уравнений
Системы линейных уравнений Устный счёт
Устный счёт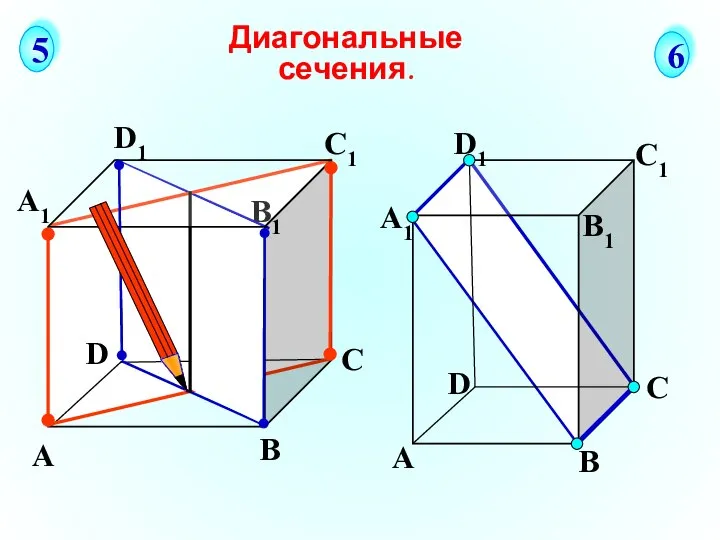 Диагональные сечения
Диагональные сечения Определение синуса, косинуса и тангенса угла
Определение синуса, косинуса и тангенса угла Метод координат
Метод координат Нахождение площади и периметра прямоугольника. Применение формул на практике
Нахождение площади и периметра прямоугольника. Применение формул на практике Взаимное расположение прямой и окружности
Взаимное расположение прямой и окружности Вычисление площадей
Вычисление площадей Производная сложной функции
Производная сложной функции Обучающие слайды
Обучающие слайды Задача на процкеты
Задача на процкеты Презентация на тему Симметрия и движение (9 класс)
Презентация на тему Симметрия и движение (9 класс)  Составление систем уравнений Колмогорова. Математическое моделирование
Составление систем уравнений Колмогорова. Математическое моделирование Математический диктант по теме: Дроби. 6 класс
Математический диктант по теме: Дроби. 6 класс Дробная схватка
Дробная схватка Линейное уравнение с одной переменной
Линейное уравнение с одной переменной Математика и здоровье. Математика и медицина
Математика и здоровье. Математика и медицина Тригонометрия. Контрольная работа
Тригонометрия. Контрольная работа Презентация на тему Центральные углы и углы, вписанные в окружность
Презентация на тему Центральные углы и углы, вписанные в окружность