Содержание
- 2. ДУ с однородной функцией нулевого порядка в правой части. (однородные уравнения первого порядка).
- 3. Функция f(x;y) называется однородной степени n, если умножение всех её аргументов на одно и то же
- 4. Пример 1. - однородная функция 3-ей степени Так как
- 5. - однородная функция 1-ой степени Так как - однородная функция 0-ой степени Так как
- 6. - однородная функция 2-ой степени Так как - однородная функция (-1)-ой степени Так как
- 7. ДУ I порядка называется однородным, если f(x;y)- однородная функция 0-ой степени, т.е.
- 8. Однородное ДУ I порядка можно записать в виде: Т.к. , то если положить Получаем:
- 9. Решение однородного ДУ I порядка Это уравнение преобразуется в уравнение с разделяющимися переменными при помощи замены
- 10. или
- 11. или -общее решение данного ДУ
- 12. Пример 2. Найти общее решение ДУ: Это однородное ДУ вида ⇒
- 15. Пример 3. Решить задачу Коши: , если y(1)=0 Это однородное ДУ вида ⇒
- 18. - общее решение Решим задачу Коши у(1)=0 : или - частное решение
- 19. Уравнение вида называется однородным уравнением в дифференциальной форме, если M(x;y) и N(x;y) - однородные функции одной
- 20. Пример 4. Найти общее решение ДУ: M(x;y) N(x;y) - однородное уравнение вида
- 21. ⇒
- 22. (*)
- 23. - общее решение
- 24. Это однородное ДУ можно привести к виду
- 25. ⇒ ⇒
- 26. - получили (*)
- 27. Пример 5. Найти общее решение ДУ: M(x;y) N(x;y) - однородное уравнение вида ⇒
- 29. Пример 6. Найти общее решение ДУ: Это однородное ДУ можно привести к виду
- 30. ⇒
- 31. общий интеграл ду
- 32. - общий интеграл или - общий интеграл
- 33. Линейные уравнения первого порядка. Уравнения Бернулли
- 34. Линейные уравнения первого порядка Линейным дифференциальным уравнением первого порядка называется ДУ 1-го порядка, линейное относительно неизвестной
- 35. y ′ + p(x) y = 0 Разделим переменные: dx dy + p( x) y =
- 36. Рассмотрим линейное неоднородное уравнение: (1) y ′ + p(x) ⋅ y = f(x) . Существуют два
- 37. y = C( x) ⋅ e−∫ p( x)dx ⇒ dx dx dy = dC ⋅ e−∫
- 38. Таким образом, общее решение линейного неоднородного уравнения (1) имеет вид: (3) (4) Заметим, что первое слагаемое
- 39. II) Метод Бернулли. Будем искать решение (1) в следующем виде: y = u(x) ⋅ v(x) .
- 40. Замечание. Линейное неоднородное уравнение вида y ′ + p(x) ⋅ y = b проще интегрировать как
- 41. Уравнения Бернулли (6) Уравнением Бернулли называется уравнение вида y ′ + p(x) ⋅ y = q(x)
- 42. 1−n Пусть z = y ⇒ dx dx dz −n dy = (1 − n) y
- 44. Скачать презентацию



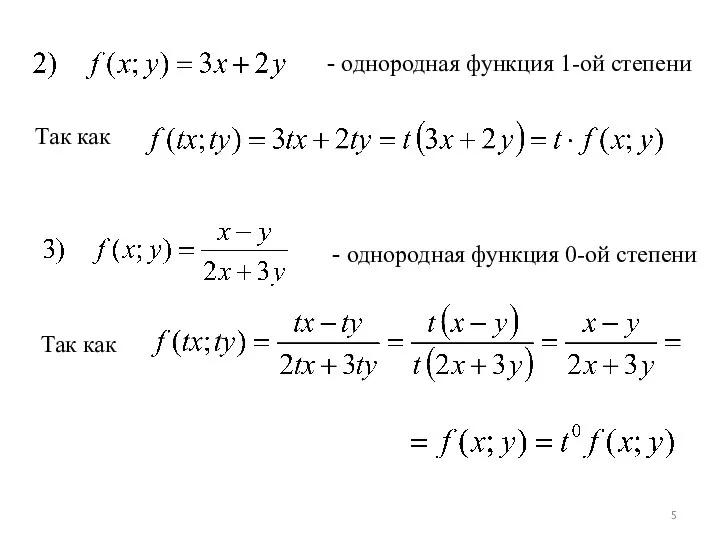
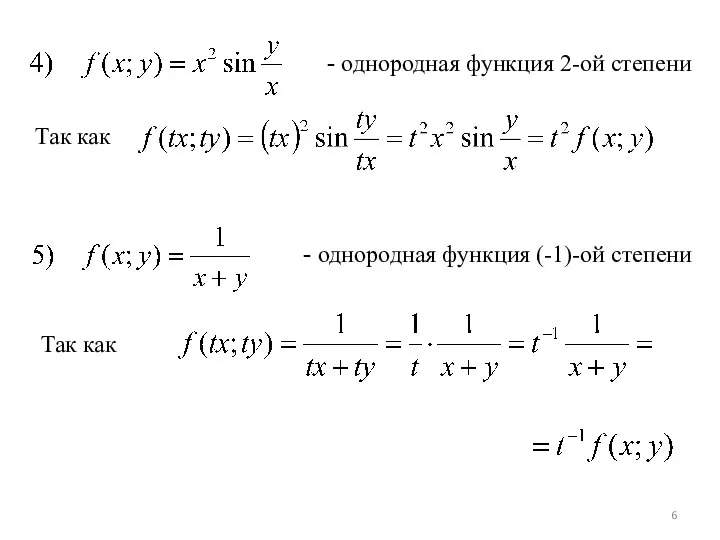



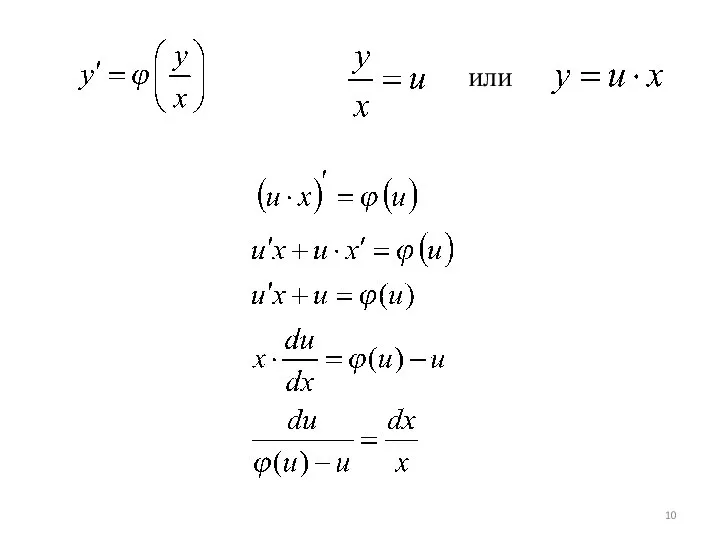


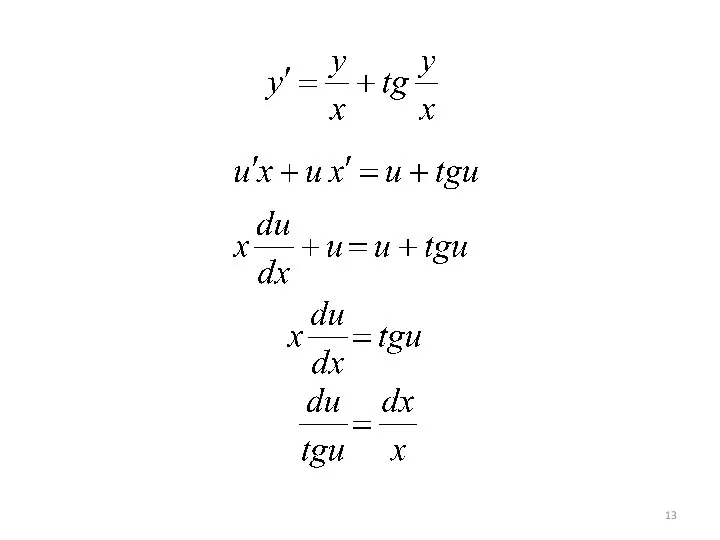
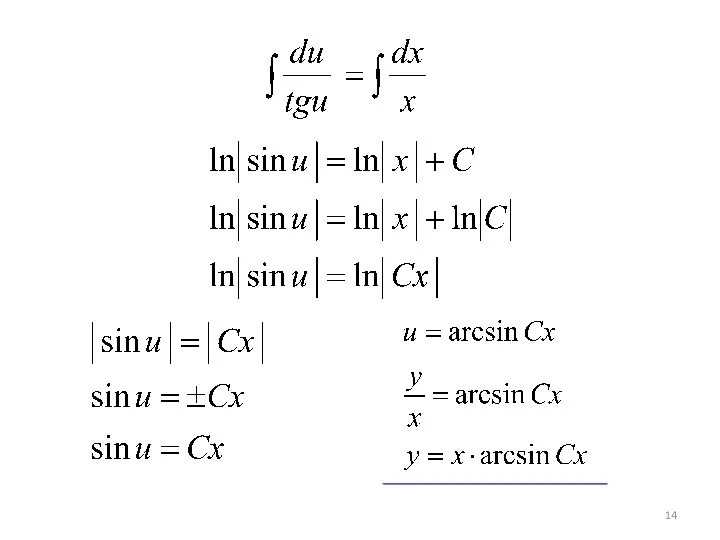

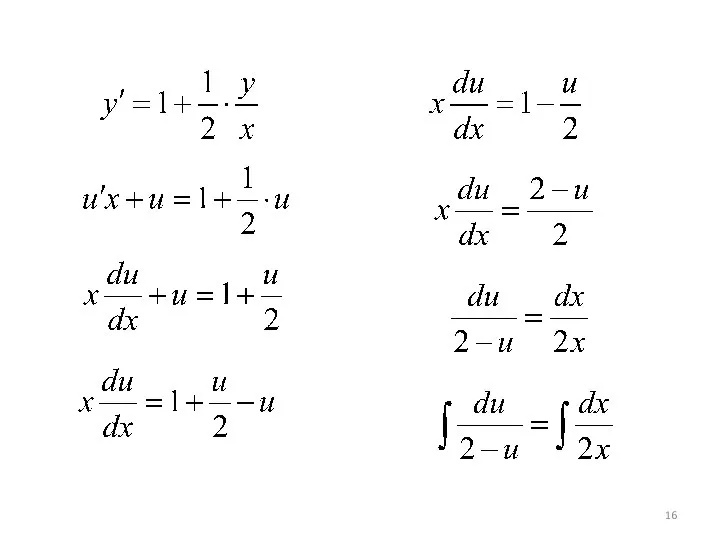
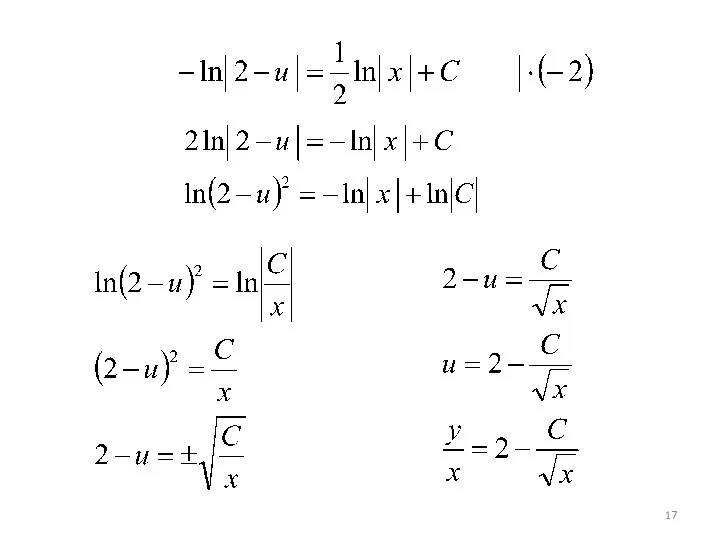



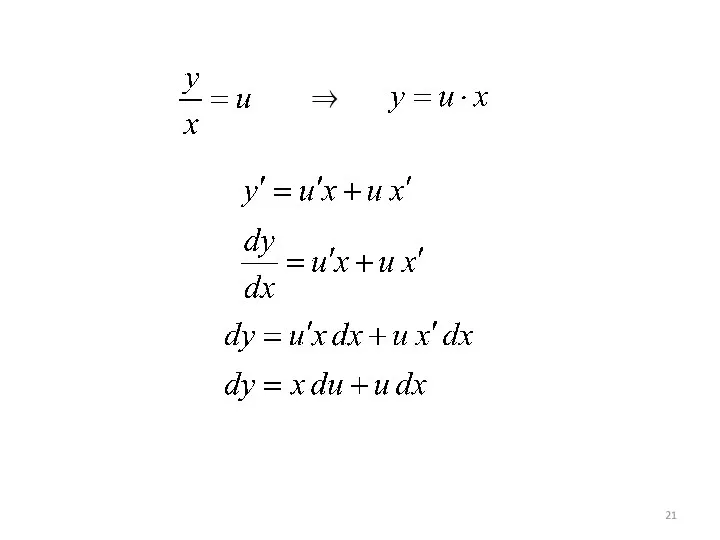
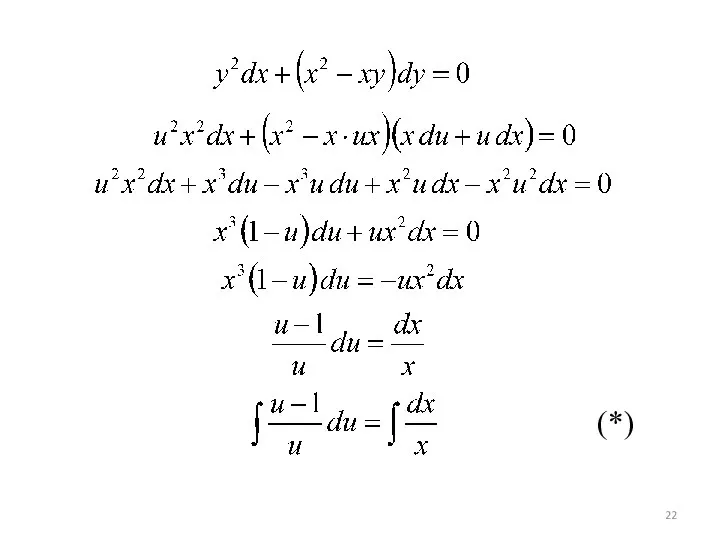


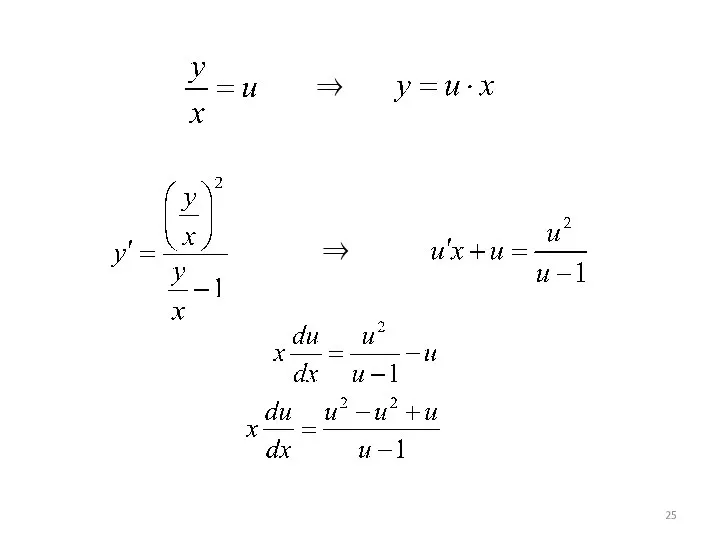




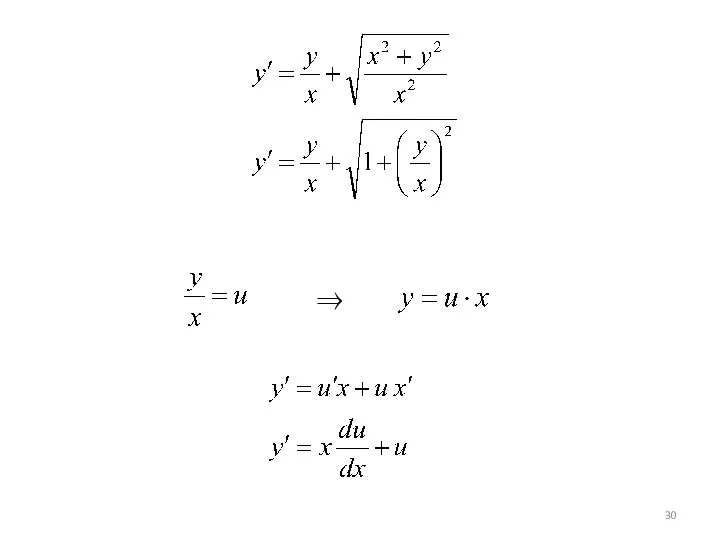












 Среднее арифметическое
Среднее арифметическое Метод неопределенных коэффициентов
Метод неопределенных коэффициентов Среднее арифметическое
Среднее арифметическое Узоры и орнаменты на посуде
Узоры и орнаменты на посуде Игра Что? Где? Почему?
Игра Что? Где? Почему? Интегрирование тригонометрических функций
Интегрирование тригонометрических функций Пирамида
Пирамида Исаак Ньютон
Исаак Ньютон Колесо истории математики
Колесо истории математики Высота, биссектриса и медиана треугольника
Высота, биссектриса и медиана треугольника Методология математического моделирования
Методология математического моделирования Тест. Реши. И ты станешь уважать себя
Тест. Реши. И ты станешь уважать себя Поле чудес. 3 класс
Поле чудес. 3 класс Нахождение коэффициентов квадратичной функции по графику
Нахождение коэффициентов квадратичной функции по графику Многогранники. Призма
Многогранники. Призма Обыкновенные дроби. 5 класс
Обыкновенные дроби. 5 класс Prezentatsia
Prezentatsia Гарри Потер. Игра по математике и физике
Гарри Потер. Игра по математике и физике Треугольники. Задача
Треугольники. Задача Производная. Физический смысл производной. Приращение аргумента и приращение функции. Задания
Производная. Физический смысл производной. Приращение аргумента и приращение функции. Задания Презентация на тему Квадратичная функция
Презентация на тему Квадратичная функция  Повторение. Дроби
Повторение. Дроби Решение задач на движение
Решение задач на движение Округление десятичных дробей
Округление десятичных дробей Перпендикулярность плоскостей. 10 класс
Перпендикулярность плоскостей. 10 класс Элементы комбинаторики
Элементы комбинаторики Урок математики в 10 классе по теме Пирамида
Урок математики в 10 классе по теме Пирамида Сокращение дробей. Тождество
Сокращение дробей. Тождество