Медианы, биссектрисы и высоты треугольника

Что это за фигура, что вы про нее знаете?

Цель урока:
Ввести понятие перпендикуляра к прямой;
Ввести понятие медианы, биссектрисы и высоты треугольника;
Отработать навыки построения медианы, биссектрисы и высоты треугольника с помощью чертёжных инструментов.

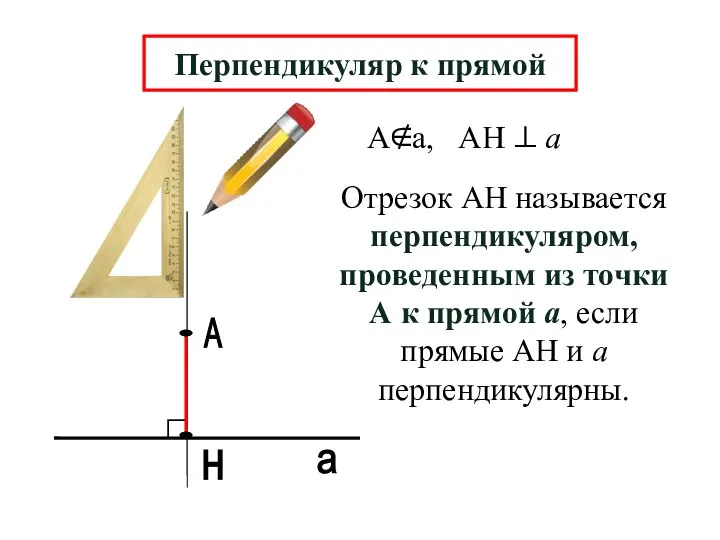
А
н
а
Перпендикуляр к прямой
Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны.
А∉а, АН ⊥ а

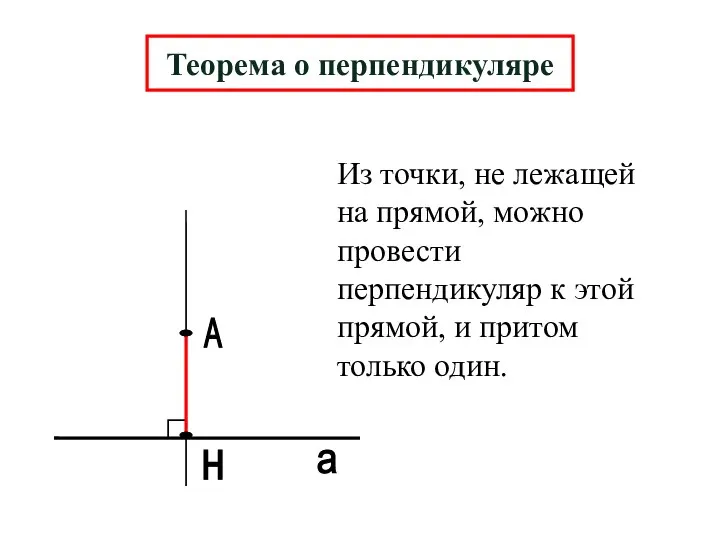
А
н
а
Теорема о перпендикуляре
Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

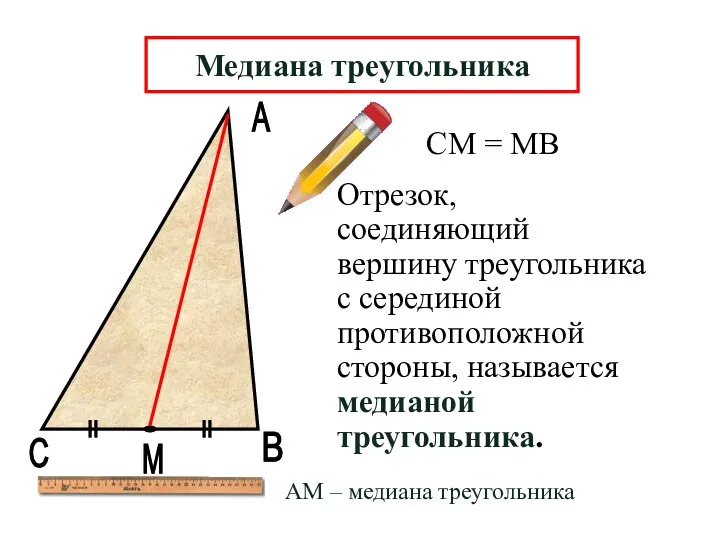
А
В
М
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
С
СМ = МВ
Медиана треугольника
АМ – медиана треугольника

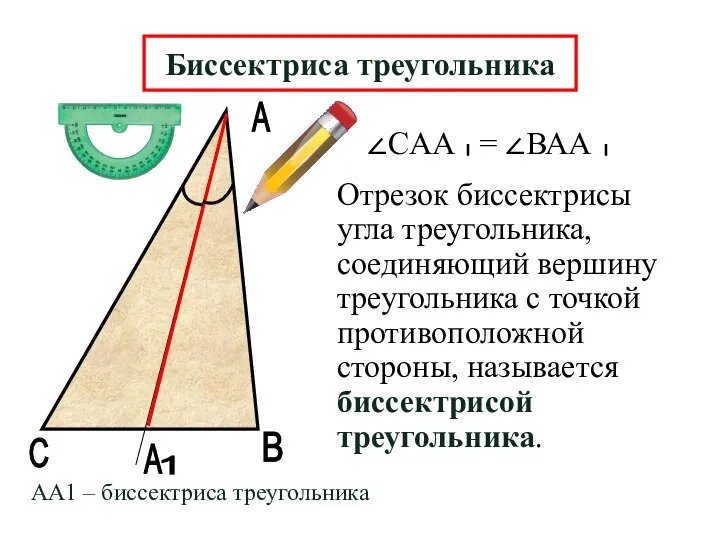
А
В
А
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.
С
1
Биссектриса треугольника
АА1 – биссектриса треугольника

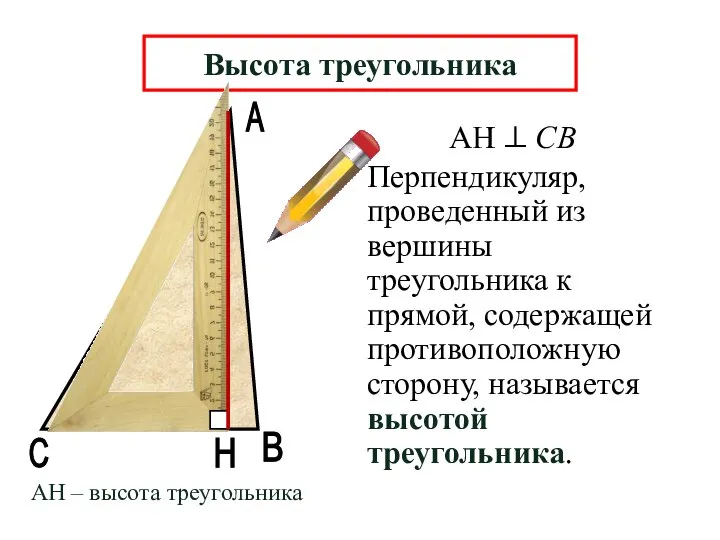
А
В
Н
Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.
С
Высота треугольника
АН – высота треугольника
АН ⊥ СВ

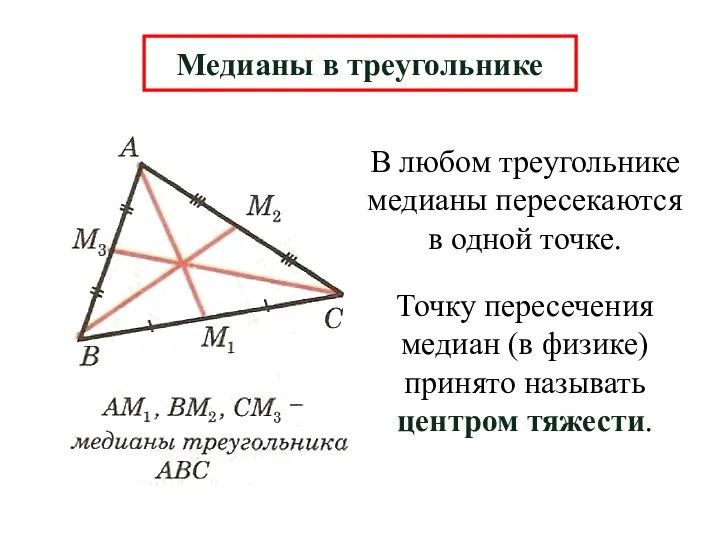
В любом треугольнике медианы пересекаются в одной точке.
Медианы в треугольнике
Точку пересечения медиан (в физике) принято называть центром тяжести.

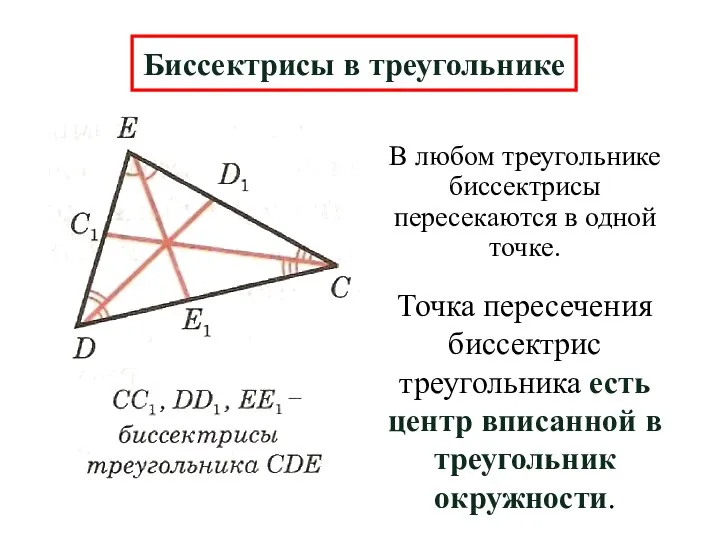
В любом треугольнике биссектрисы пересекаются в одной точке.
Биссектрисы в треугольнике
Точка пересечения биссектрис треугольника есть центр вписанной в треугольник окружности.

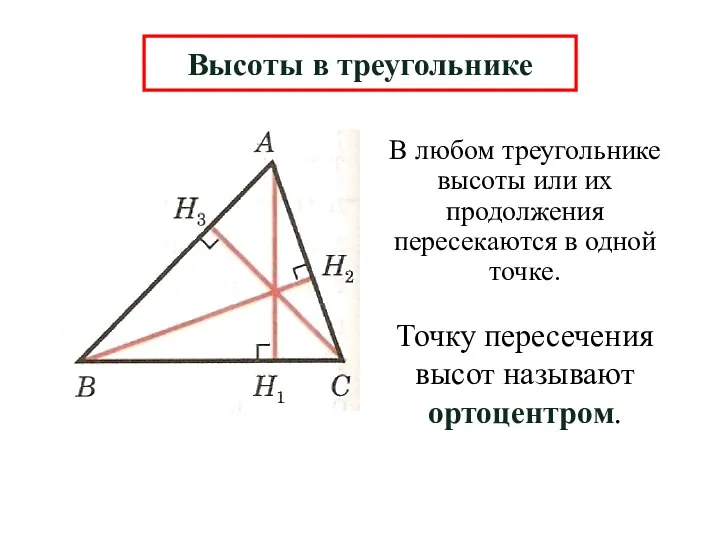
Высоты в треугольнике

В любом треугольнике высоты или их продолжения пересекаются в одной точке.
Высоты в треугольнике
Точку пересечения высот называют ортоцентром.

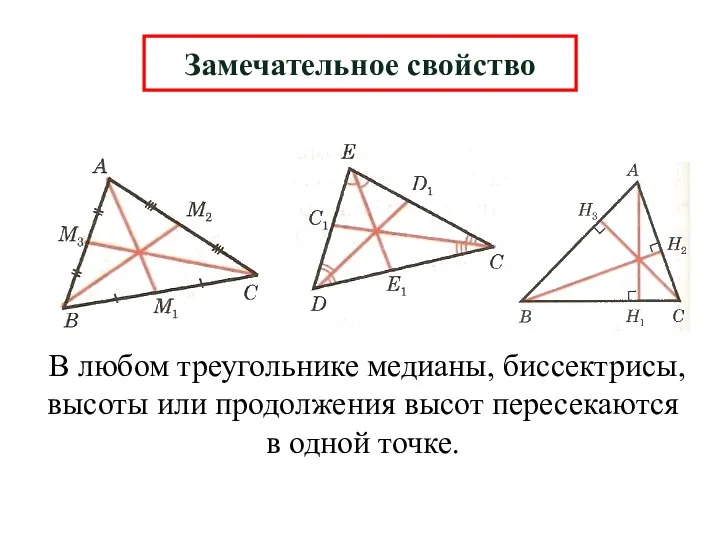
Замечательное свойство
В любом треугольнике медианы, биссектрисы, высоты или продолжения высот пересекаются в одной точке.