Понятие многогранника, призмы и их элементов

Цель: ввести понятие многогранника, призмы и их элементов
Учебно – познавательная: формирование умений применять основные понятия многогранника, призмы и их элементов при решении задач на конструктивном уровне
Задачи:
Развивающая: развитие визуального, наглядно-образного типов мышления.
Воспитательная: способствовать развитию устойчивого интереса к математике через применение информационно – коммуникационных технологий.

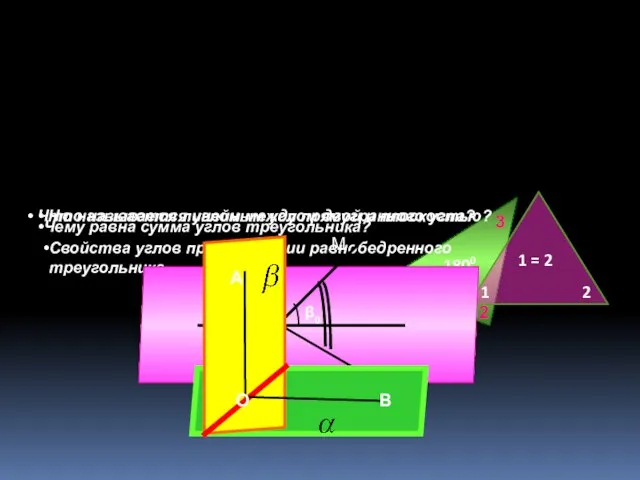
Чему равна сумма углов треугольника?
1
2
3
1800
Свойства углов при основании равнобедренного треугольника.
1
2
1 = 2 Что называется углом между прямой и плоскостью?
М
А
β0
Что называется линейным углом двугранного угла?
А
В
О

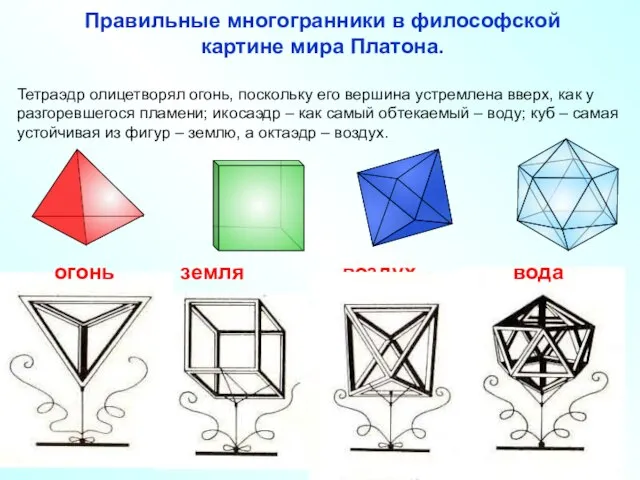
Правильные многогранники в философской
картине мира Платона.
Тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх, как у разгоревшегося пламени; икосаэдр – как самый обтекаемый – воду; куб – самая устойчивая из фигур – землю, а октаэдр – воздух.

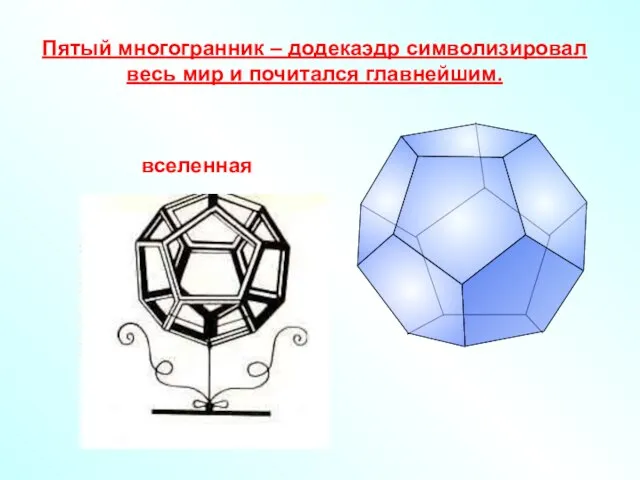
Пятый многогранник – додекаэдр символизировал весь мир и почитался главнейшим.

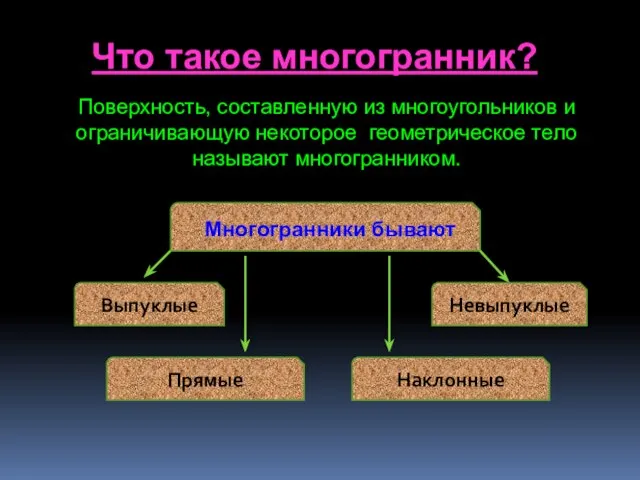
Что такое многогранник?
Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело называют многогранником.
Многогранники бывают
Выпуклые
Невыпуклые
Прямые
Наклонные

Прямые и наклонные многогранники

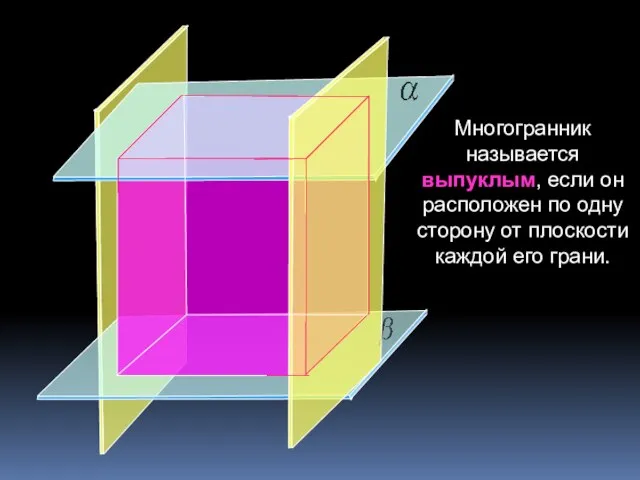
Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани.

Невыпуклый многогранник

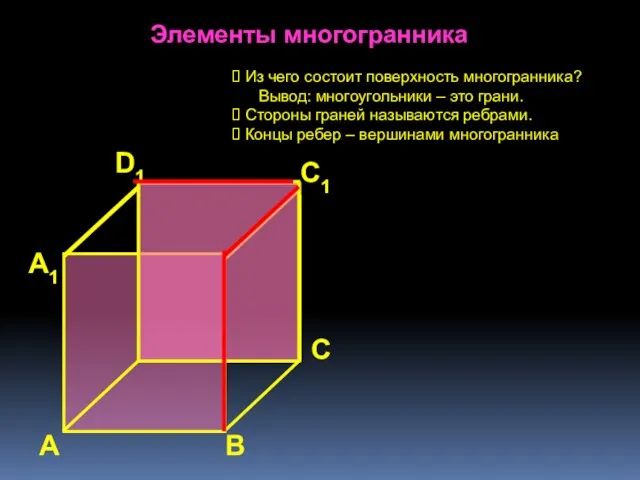
А
А1
С1
D1
С
В
Элементы многогранника
Из чего состоит поверхность многогранника?
Вывод: многоугольники – это грани.
Стороны граней называются ребрами.
Концы ребер – вершинами многогранника

Свойства плоских углов многогранника
При одной вершине сходится n плоских углов, но чтобы образовался многогранный угол сумма их градусных мер должна быть меньше 360°, т.е.
nα< 360°
Угол правильного треугольника равен 60°, значит в
одной вершине может сходиться
3, 4 или 5 правильных треугольников
Тетраэдр
Октаэдр
Икосаэдр
Существуют многогранники, гранями которых являются правильные треугольники
Угол квадрата равен 90°, значит в одной вершине может сходиться только 3 квадрата
Существуют многогранники, гранями которых являются правильные четырёхугольники
Гексаэдр
Угол правильного пятиугольника равен 108°, значит в одной вершине может сходиться только 3 правильных
пятиугольника
Существуют многогранники, гранями которых являются правильные пятиугольники
Додекаэдр

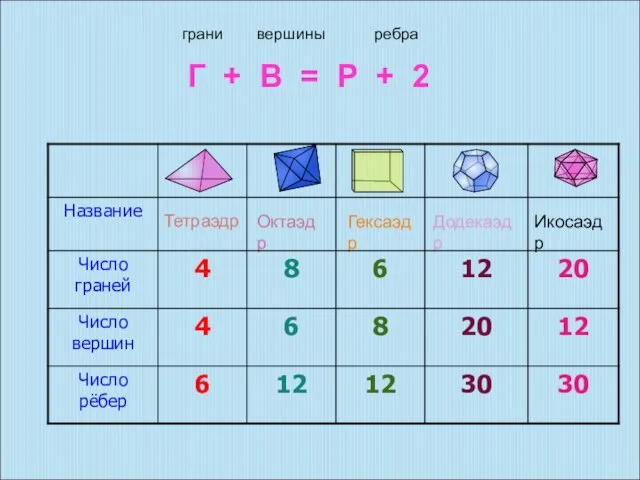
Эйлерова
характеристика многогранника
В каждом правильном многограннике сумма числа и вершин равна числу рёбер, увеличенному на 2.
60°+ 60° + 60° < 360°
4 грани, 4 вершины и 6 ребер.
Сумма плоских углов при каждой вершине равна 1800

Тетраэдр
Октаэдр
Гексаэдр
Додекаэдр
Икосаэдр

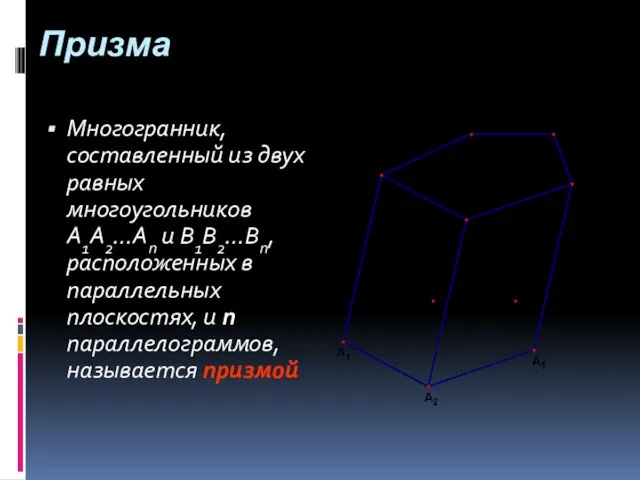
Призма
Многогранник, составленный из двух равных многоугольников A1A2…An и B1B2…Bn, расположенных в параллельных плоскостях, и n параллелограммов, называется призмой

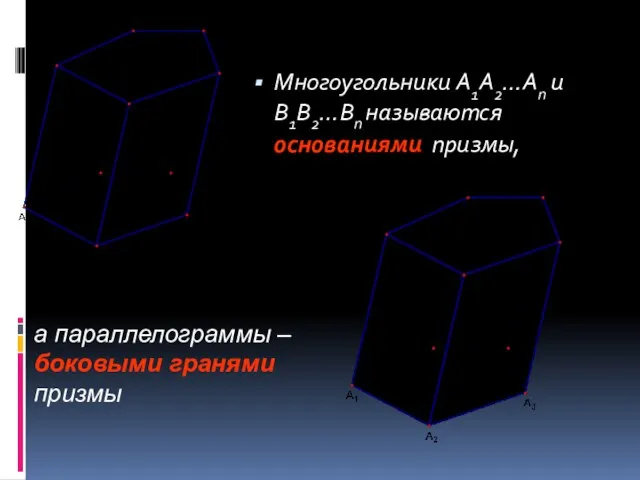
Многоугольники A1A2…An и B1B2…Bn называются основаниями призмы,
а параллелограммы – боковыми гранями призмы

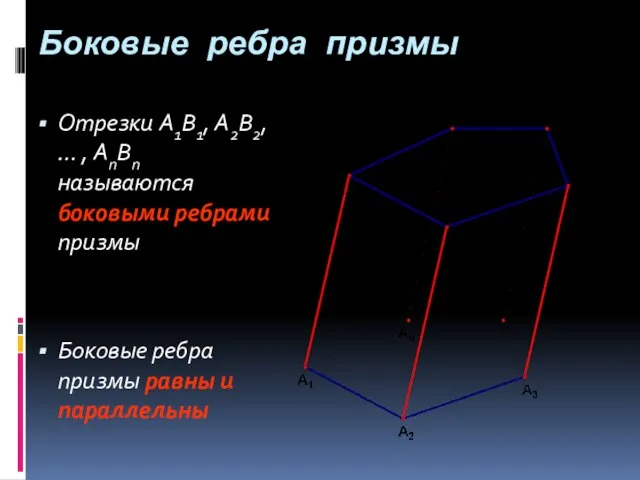
Отрезки A1B1, A2B2, … , AnBn называются боковыми ребрами призмы
Боковые ребра призмы равны и параллельны
Боковые ребра призмы

Призму с основаниями A1A2…An и B1B2…Bn обозначают A1A2…AnB1B2…Bn и называют n-угольной призмой

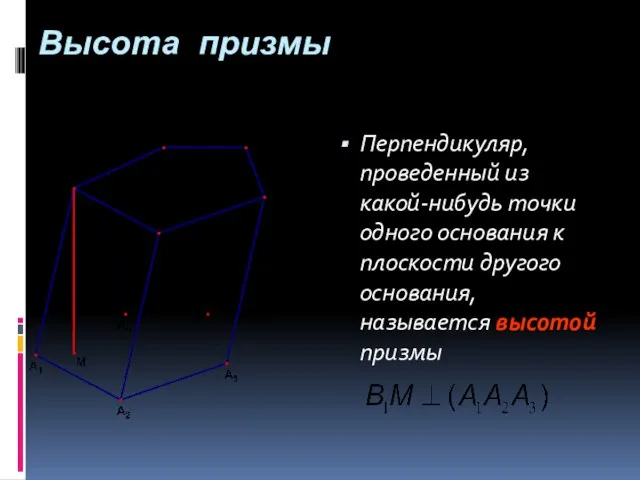
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы
Высота призмы

Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой,
в противном случае – наклонной
Высота прямой призмы равна её боковому ребру
Прямая и наклонная призмы

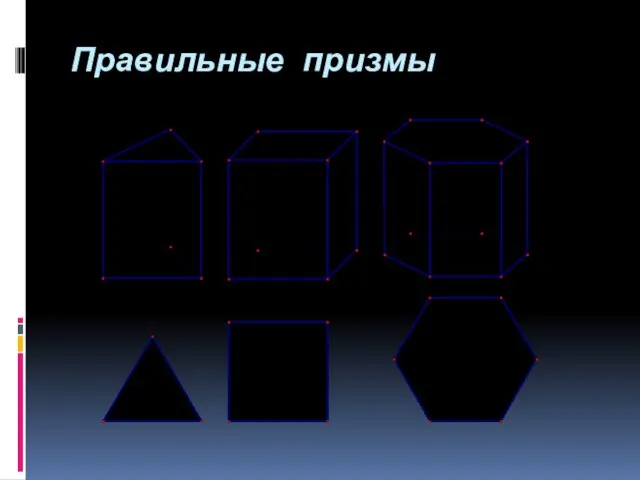
Правильная призма
Прямая призма называется правильной, если её основания – правильные многоугольники
У правильной призмы все боковые грани – равные прямоугольники

Правильные призмы

Параллелепипед
Если основания призмы - параллелограммы, то призма является параллелепипедом
В параллелепипеде все грани являются параллелограммами

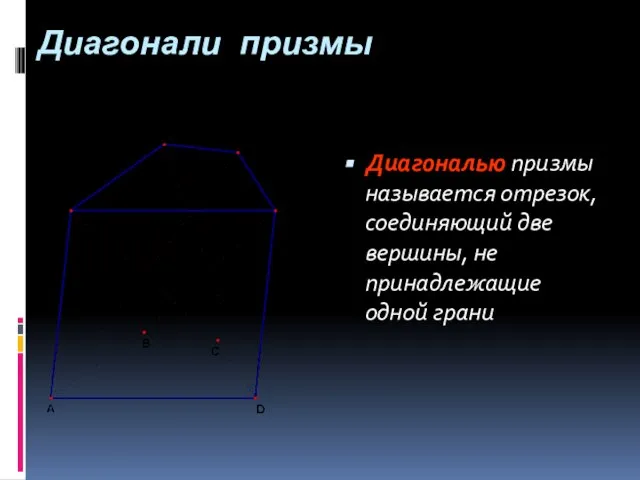
Диагонали призмы
Диагональю призмы называется отрезок, соединяющий две вершины, не принадлежащие одной грани

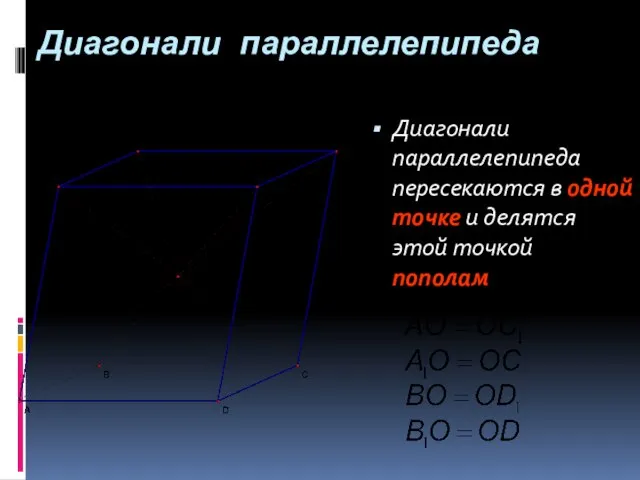
Диагонали параллелепипеда
Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам

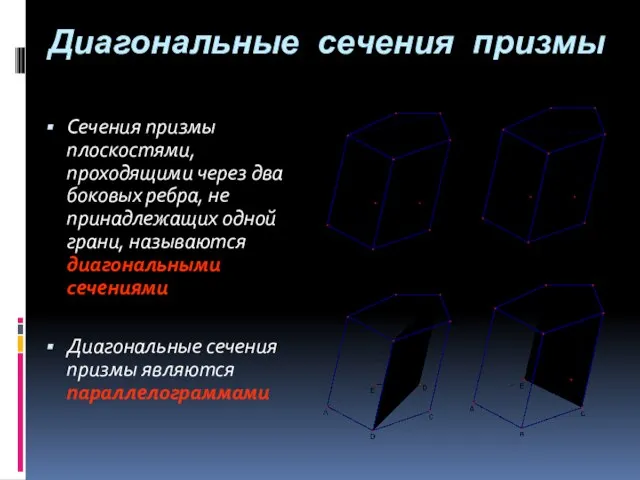
Диагональные сечения призмы
Сечения призмы плоскостями, проходящими через два боковых ребра, не принадлежащих одной грани, называются диагональными сечениями
Диагональные сечения призмы являются параллелограммами

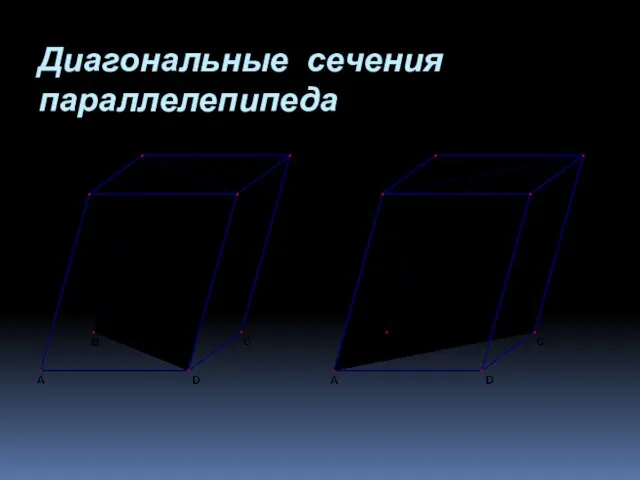
Диагональные сечения
параллелепипеда

Площадь поверхности призмы
Площадью полной поверхности призмы называется сумма площадей всех её граней
Площадью боковой поверхности призмы называется сумма площадей её боковых граней

Теорема о площади боковой поверхности прямой призмы
Теорема.
Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы

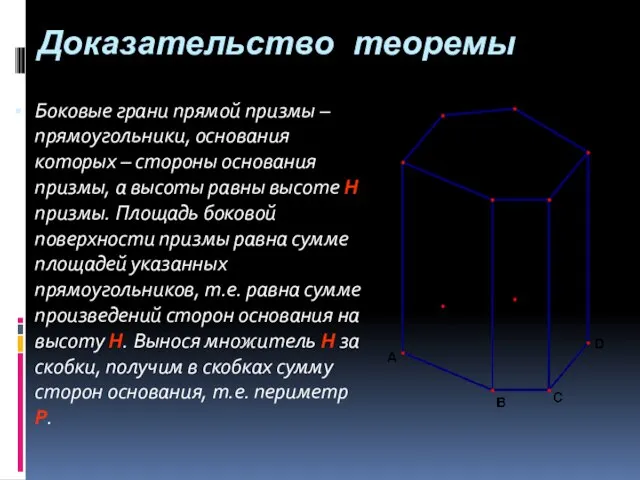
Доказательство теоремы
Боковые грани прямой призмы – прямоугольники, основания которых – стороны основания призмы, а высоты равны высоте H призмы. Площадь боковой поверхности призмы равна сумме площадей указанных прямоугольников, т.е. равна сумме произведений сторон основания на высоту H. Вынося множитель H за скобки, получим в скобках сумму сторон основания, т.е. периметр P.

Умение решать задачи – практическое искусство, подобное плаванию, или катанию на лыжах … : научиться этому можно лишь подражая избранным
образцам и постоянно тренируясь..
Д. Пойа

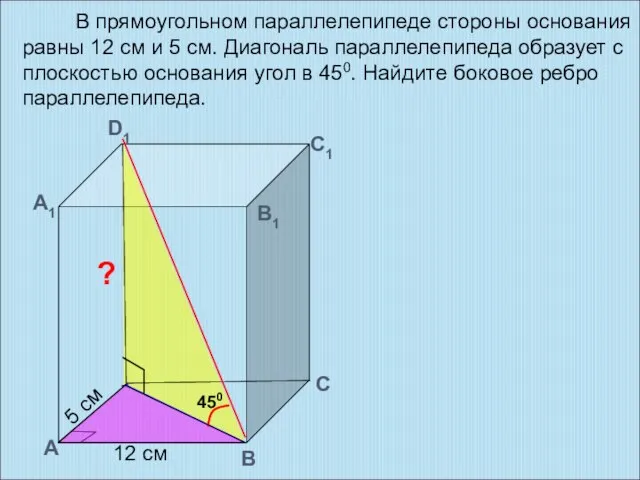
В прямоугольном параллелепипеде стороны основания равны 12 см и 5 см. Диагональ параллелепипеда образует с плоскостью основания угол в 450. Найдите боковое ребро параллелепипеда.
В
С
А1
D1
С1
В1
?
А
12 см
5 см

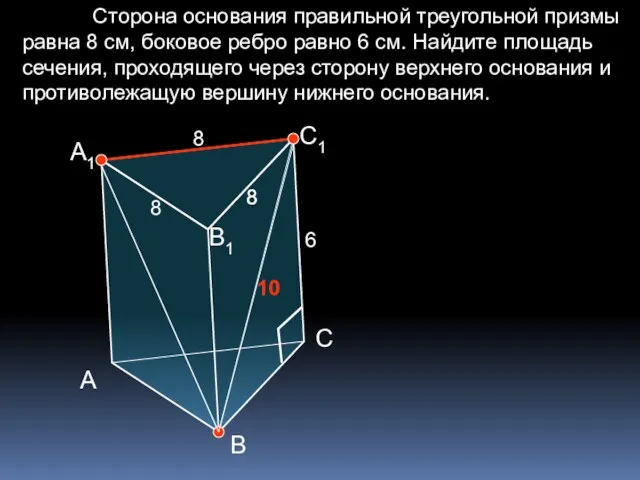
Сторона основания правильной треугольной призмы равна 8 см, боковое ребро равно 6 см. Найдите площадь сечения, проходящего через сторону верхнего основания и противолежащую вершину нижнего основания.
А
В
С
С1
В1
А1
8
6
8
8
8
10

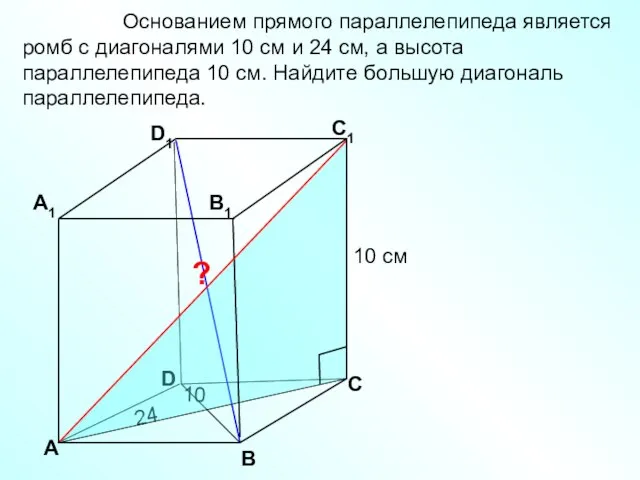
Основанием прямого параллелепипеда является ромб с диагоналями 10 см и 24 см, а высота параллелепипеда 10 см. Найдите большую диагональ параллелепипеда.
В
С
А1
D1
С1
В1
?
D
А
24
10
10 см