Табличный метод решения задач ЕГЭ по теории вероятностей

Задания B6

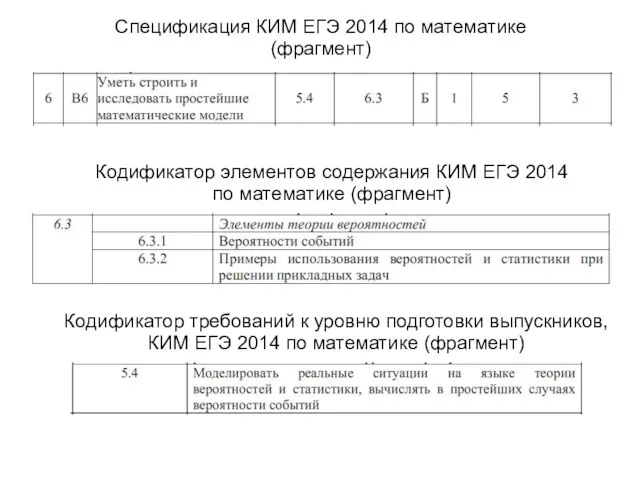
Спецификация КИМ ЕГЭ 2014 по математике
(фрагмент)
Кодификатор элементов содержания КИМ ЕГЭ 2014
по математике (фрагмент)
Кодификатор требований к уровню подготовки выпускников, КИМ ЕГЭ 2014 по математике (фрагмент)

Основные теоремы
Если события А и B независимы, то

Задача 1. Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, то она получает 3 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,3.

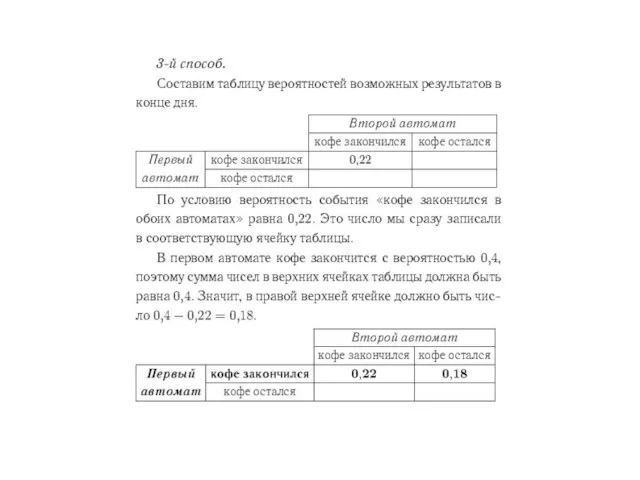
Задача 2. В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.

Задача 3. Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция» нужно набрать не менее 70 баллов по каждому из трёх предметов — математика, русский язык и обществознание.
Вероятность того, что абитуриент А. получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5.
Найдите вероятность того, что А. сможет поступить хотя бы на одну из двух упомянутых специальностей.

Задача 4. Вероятность того, что новая кофемолка прослужит больше года, равна 0,93. Вероятность того, что она прослужит больше двух лет, равна 0,81. Найдите вероятность того, что кофемолка прослужит меньше двух лет, но больше года.

Задача 5. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 24-х пассажиров, равна 0,57. Вероятность того, что окажется меньше 17-ти пассажиров, равна 0,28. Найдите вероятность того, что число пассажиров будет от 17 до 23.

Задача 6. Ковбой Билл попадает в муху на стене с вероятностью 0,8, если стреляет из пристрелянного револьвера. Если Билл стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,25. На столе лежит 5 револьверов, из них только 2 пристрелянные. Ковбой Билл видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Билл попадёт в муху.

Задача 7. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 60% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 40% яиц высшей категории. Всего высшую категорию получает 48% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.

Задача 8. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,4. Вероятность того, что кофе закончится в обоих автоматах, равна 0,22. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

Задача 9. В Волшебной стране бывает два типа погоды: хорошая и отличная, причем погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,9 погода завтра будет такой же, как и сегодня. Сегодня 11 марта, погода в Волшебной стране хорошая. Найдите вероятность того, что 14 марта в Волшебной стране будет отличная погода.

Принципы составления таблиц вероятностей