Содержание
- 2. Л. КЭРРОЛЛ “Правильных многогранников так мало, но это весьма скромный по численности отряд сумел пробраться в
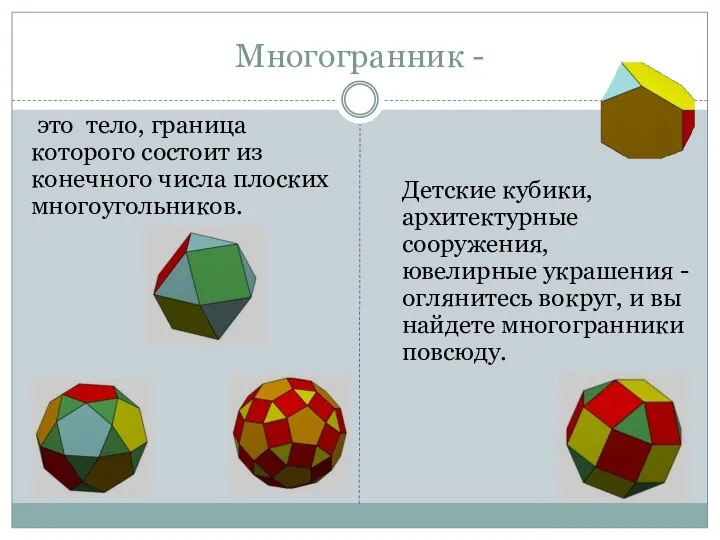
- 3. Многогранник - это тело, граница которого состоит из конечного числа плоских многоугольников. Детские кубики, архитектурные сооружения,
- 4. часть пространства, ограниченная совокупностью конечного числа плоских многоугольников, соединенных таким образом, что каждая сторона любого многоугольника
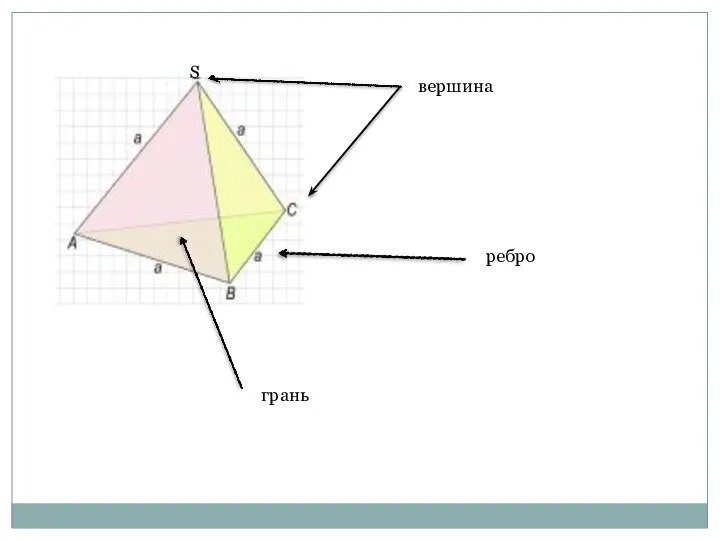
- 5. вершина ребро грань S
- 6. Пространственным аналогом правильного многоугольника на плоскости является многогранник МНОГОУГОЛЬНИК ВЕРШИНА СТОРОНА УГОЛ МНОГОГРАННИК РЕБРО ГРАНЬ ДВУГРАННЫЙ
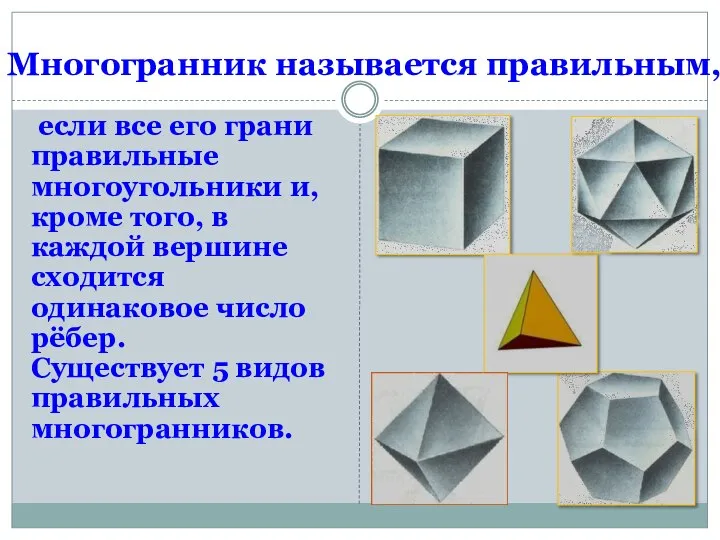
- 7. Многогранник называется правильным, если все его грани правильные многоугольники и, кроме того, в каждой вершине сходится
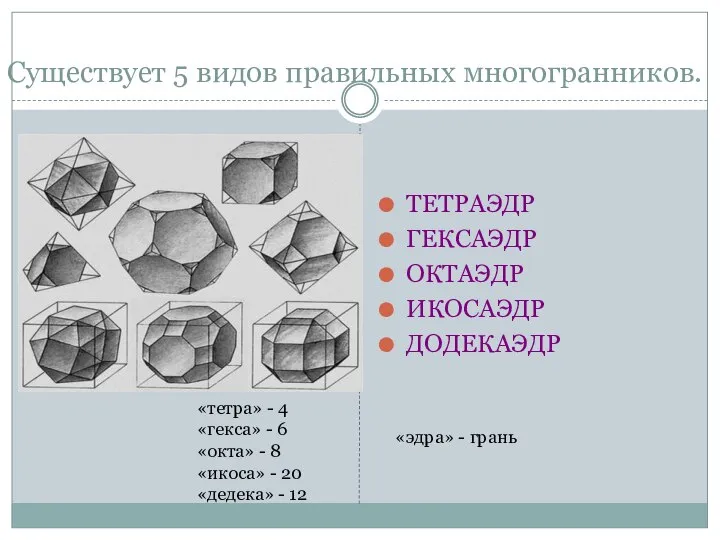
- 8. Существует 5 видов правильных многогранников. ТЕТРАЭДР ГЕКСАЭДР ОКТАЭДР ИКОСАЭДР ДОДЕКАЭДР «тетра» - 4 «гекса» - 6
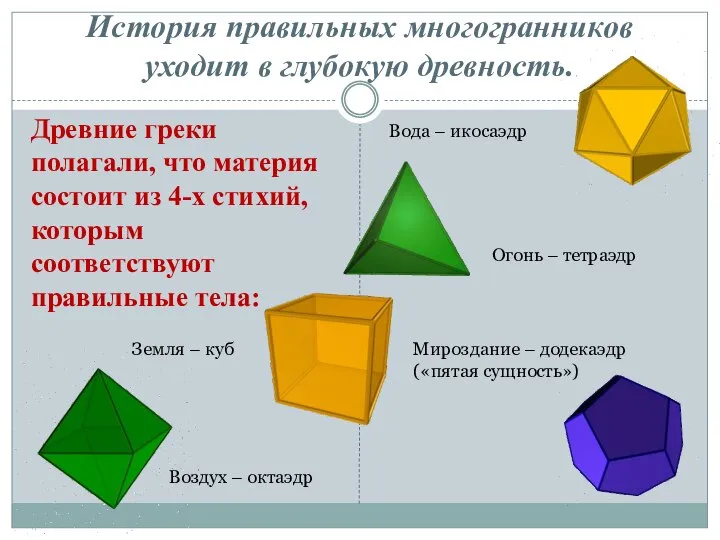
- 9. История правильных многогранников уходит в глубокую древность. Древние греки полагали, что материя состоит из 4-х стихий,
- 10. Все использовали в своих философских теориях правильные многогранники. Платон Евклид Архимед Кеплер
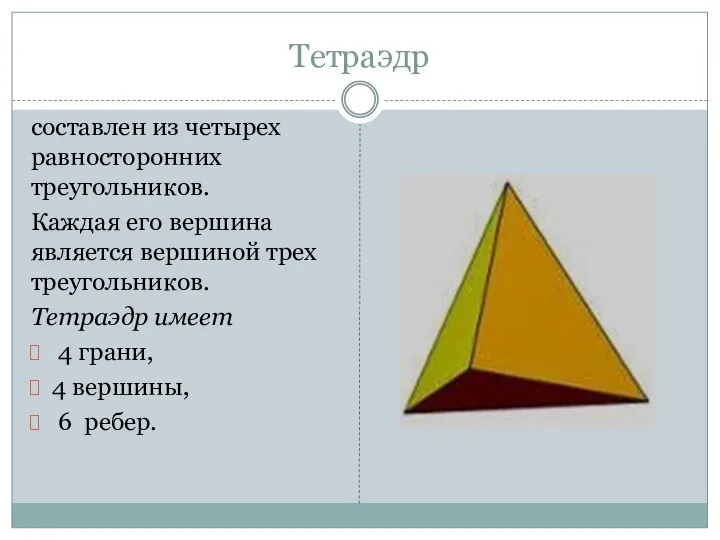
- 11. Тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Тетраэдр имеет 4
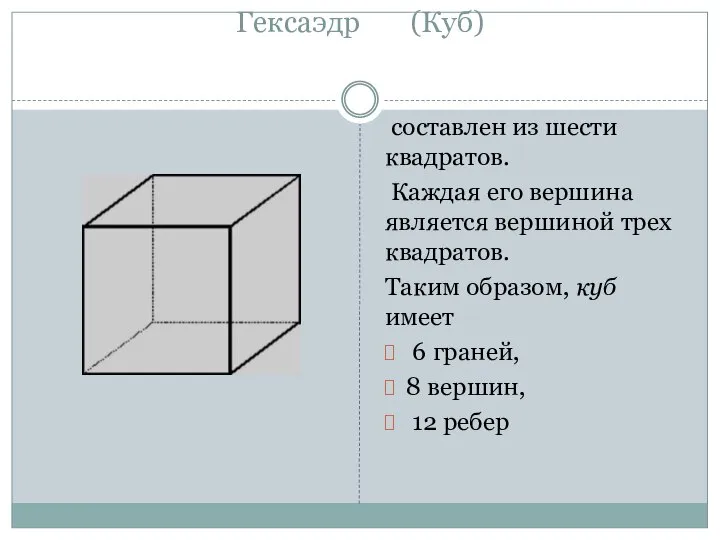
- 12. Гексаэдр (Куб) составлен из шести квадратов. Каждая его вершина является вершиной трех квадратов. Таким образом, куб
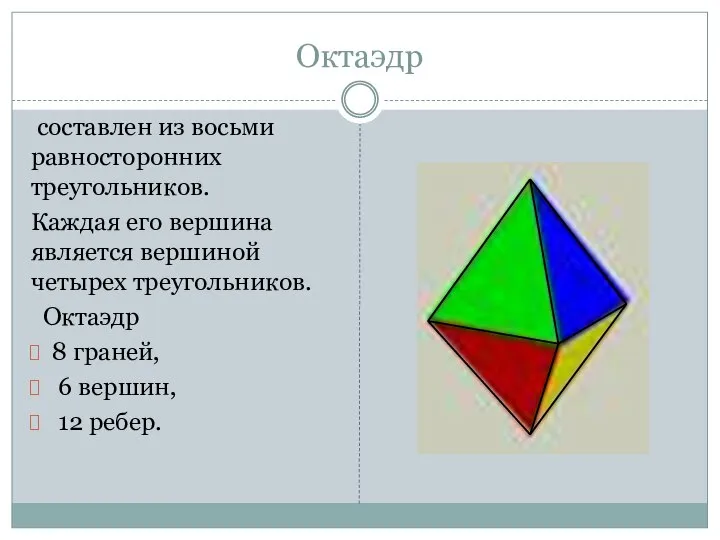
- 13. Октаэдр составлен из восьми равносторонних треугольников. Каждая его вершина является вершиной четырех треугольников. Октаэдр 8 граней,
- 14. Икосаэдр составлен из двадцати равносторонних треугольников. Каждая его вершина является вершиной пяти треугольников. Икосаэдр имеет 20
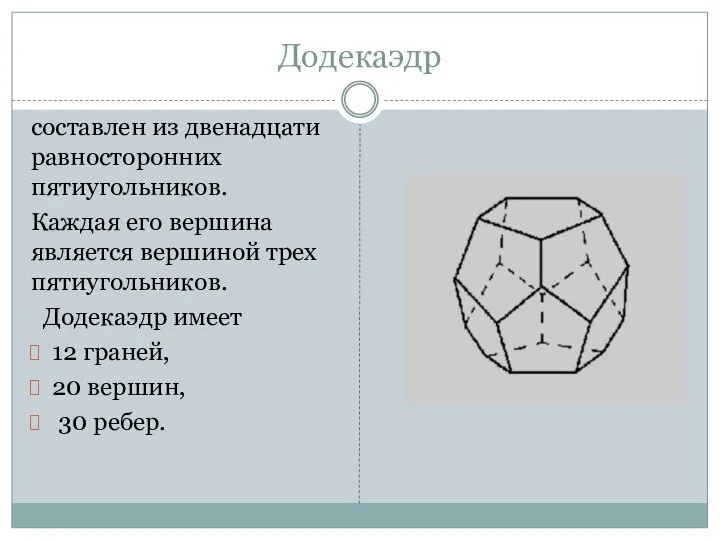
- 15. Додекаэдр составлен из двенадцати равносторонних пятиугольников. Каждая его вершина является вершиной трех пятиугольников. Додекаэдр имеет 12
- 16. В каждом правильном многограннике сумма числа граней и вершин равна числу рёбер, увеличенному на 2. Г+В=Р+2
- 18. Скачать презентацию





 Понятие функции
Понятие функции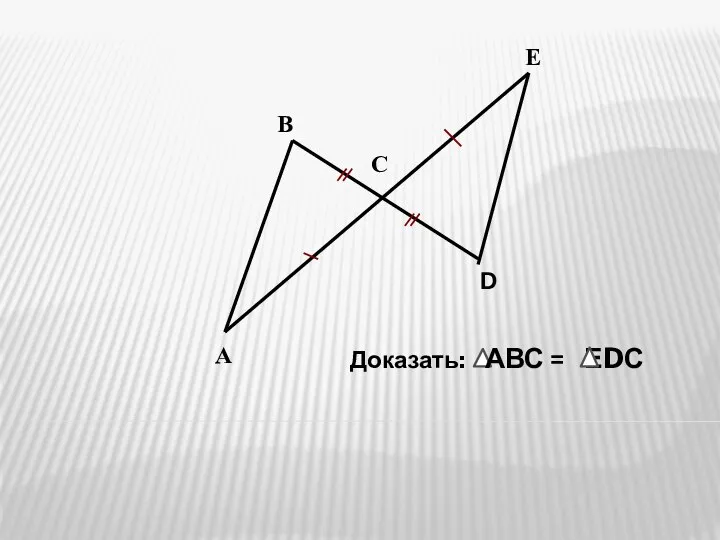 Признаки равенства треугольников. Решение задач
Признаки равенства треугольников. Решение задач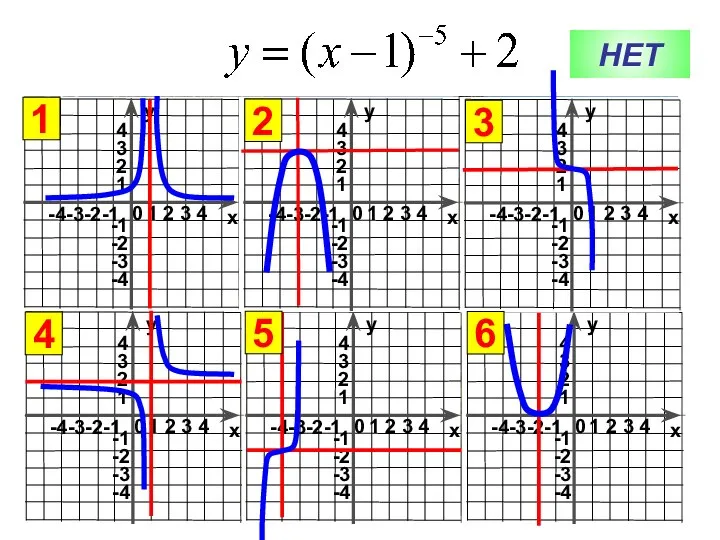 графики функций. Ошибка
графики функций. Ошибка Методы решения Слау. Метод Гаусса
Методы решения Слау. Метод Гаусса Variācijas, permutācijas, kombinācijas
Variācijas, permutācijas, kombinācijas Задачи на разрезание и перекраивание фигур
Задачи на разрезание и перекраивание фигур Презентация на тему Действия с векторами
Презентация на тему Действия с векторами  Приложение производной
Приложение производной Вычитание числа 2 (1 класс)
Вычитание числа 2 (1 класс) Допуски линейных размеров. Квалитет
Допуски линейных размеров. Квалитет Симметрия в природе
Симметрия в природе Решение задач на применение свойств прямоугольного треугольника. 7 класс
Решение задач на применение свойств прямоугольного треугольника. 7 класс Числовой коэффициент
Числовой коэффициент Квадратные уравнения. Устная разминка
Квадратные уравнения. Устная разминка Формула Стирлинга
Формула Стирлинга Старинные единицы измерения. Меры и массы и объемы
Старинные единицы измерения. Меры и массы и объемы Тригонометрические уравнения
Тригонометрические уравнения Сравнение двух прогрессий
Сравнение двух прогрессий Математика. Составные высказывания
Математика. Составные высказывания Множества точек на координатной плоскости, расстояние между точками координатной прямой
Множества точек на координатной плоскости, расстояние между точками координатной прямой Некоторые понятия о статистике, статистическом методе и термодинамике
Некоторые понятия о статистике, статистическом методе и термодинамике Математическая викторина (начальная школа)
Математическая викторина (начальная школа) Координатный луч
Координатный луч Векторы плоскости
Векторы плоскости Обыкновенные дроби. 5 класс
Обыкновенные дроби. 5 класс Площади четырёхугольников. Решение задач
Площади четырёхугольников. Решение задач Математика и физика здоровья
Математика и физика здоровья Решение задач на нахождение неизвестного вычитаемого
Решение задач на нахождение неизвестного вычитаемого