Содержание
- 2. Представим себе, что нам известен график некоторой функции f(x), который мы договоримся называть «старым» и будем
- 3. Введение Мы с вами научимся строить графики различных элементарных функций без применения производной. Такие методы построения
- 4. Укажем правила построения Гg из Гf в зависимости от того, каким образом связаны f(x) и g(x)
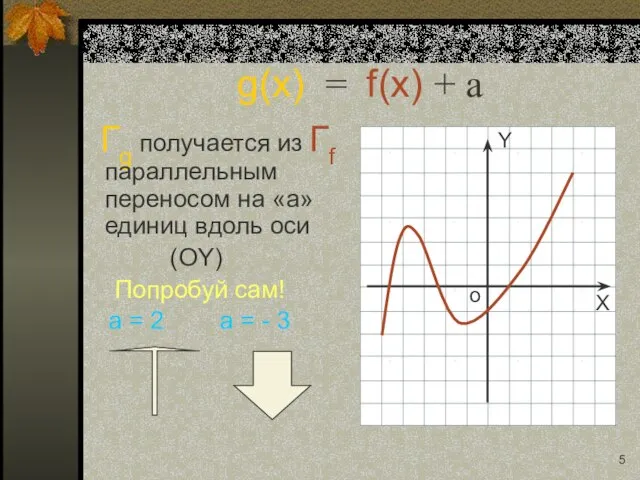
- 5. g(x) = f(x) + a Гg получается из Гf параллельным переносом на «a» единиц вдоль оси
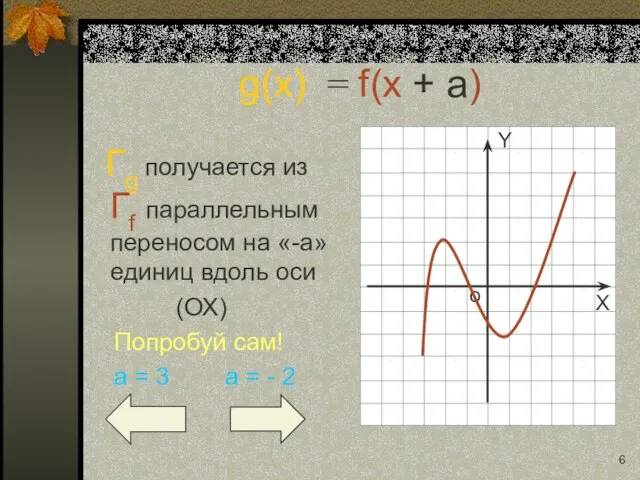
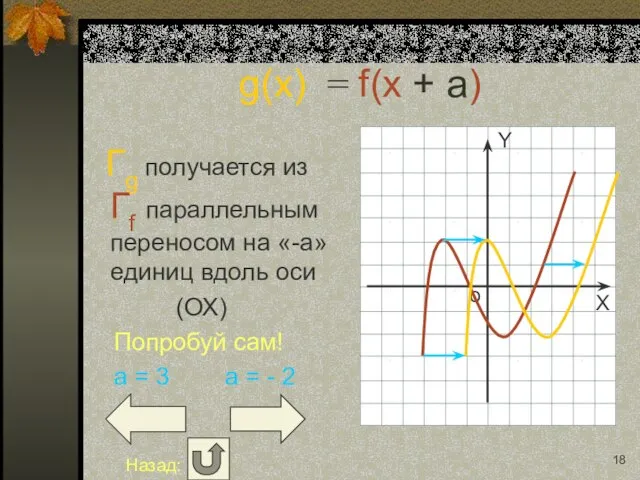
- 6. g(x) = f(x + a) Гg получается из Гf параллельным переносом на «-a» единиц вдоль оси
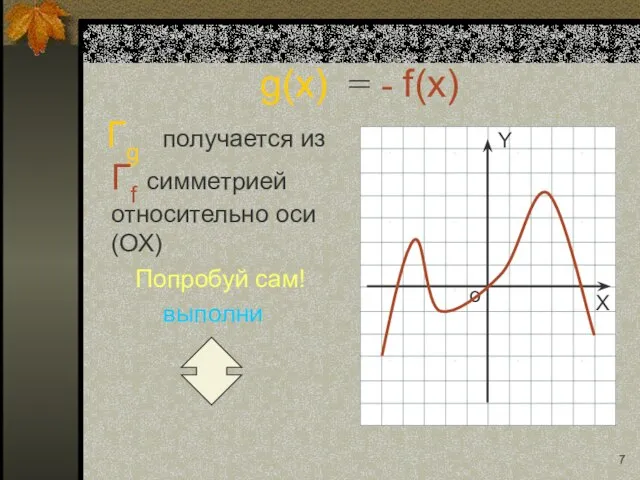
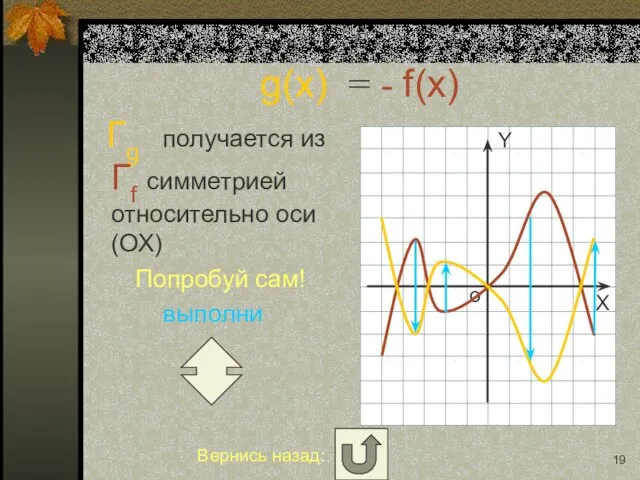
- 7. g(x) = - f(x) Гg получается из Гf симметрией относительно оси (ОХ) Попробуй сам! выполни
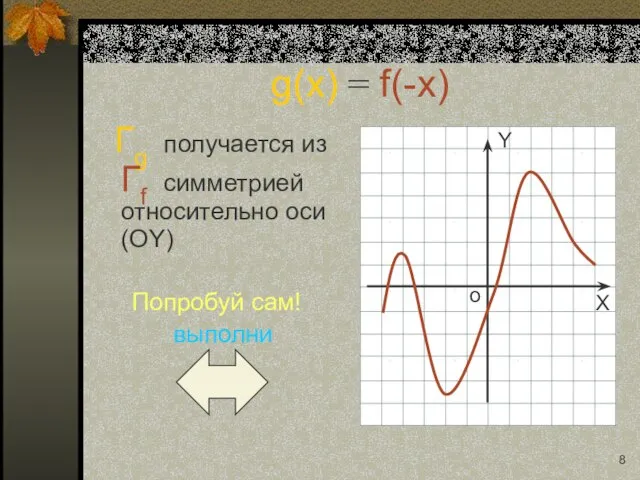
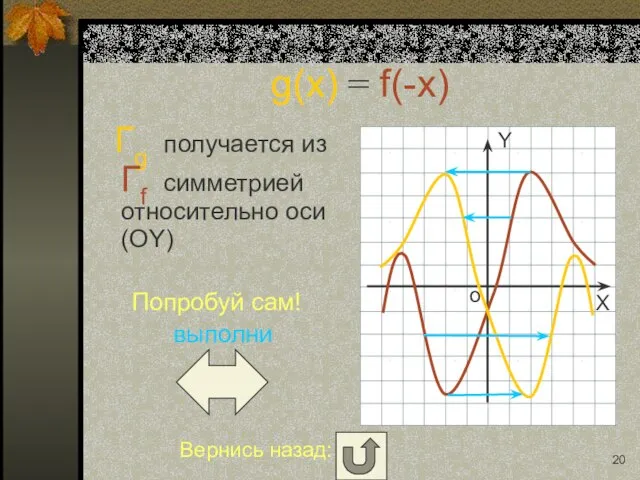
- 8. g(x) = f(-x) Гg получается из Гf симметрией относительно оси (OY) Попробуй сам! выполни
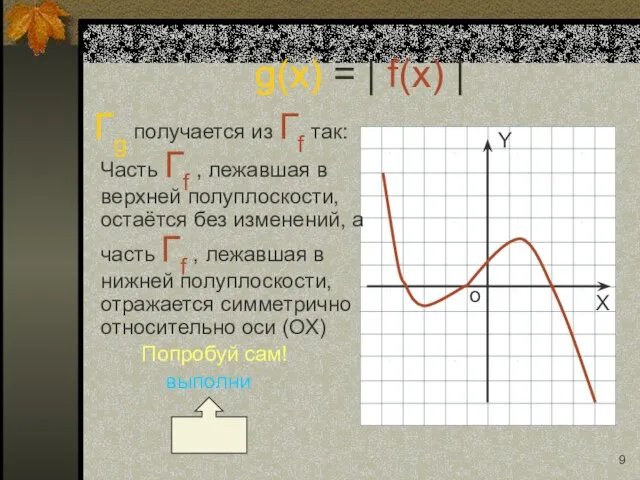
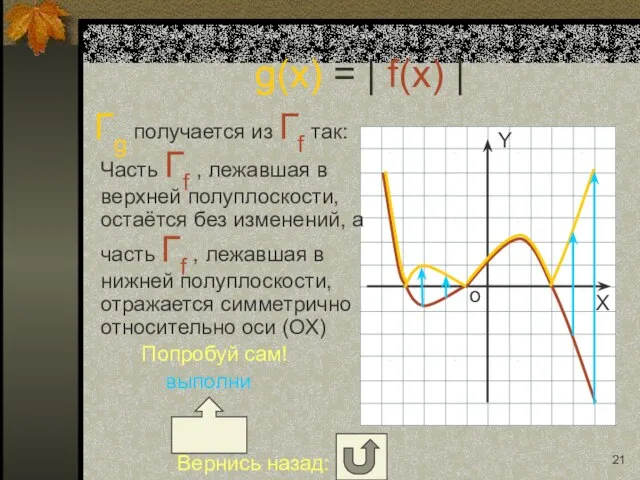
- 9. Гg получается из Гf так: Часть Гf , лежавшая в верхней полуплоскости, остаётся без изменений, а
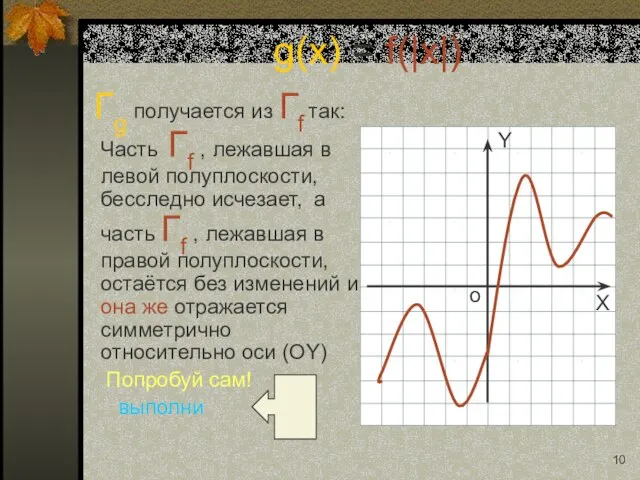
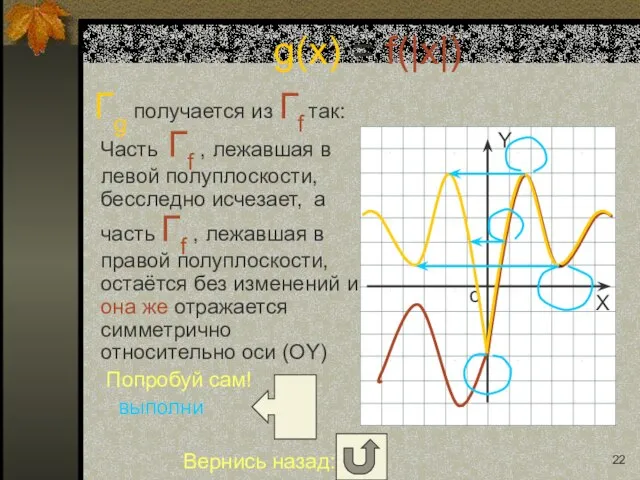
- 10. Гg получается из Гf так: Часть Гf , лежавшая в левой полуплоскости, бесследно исчезает, а часть
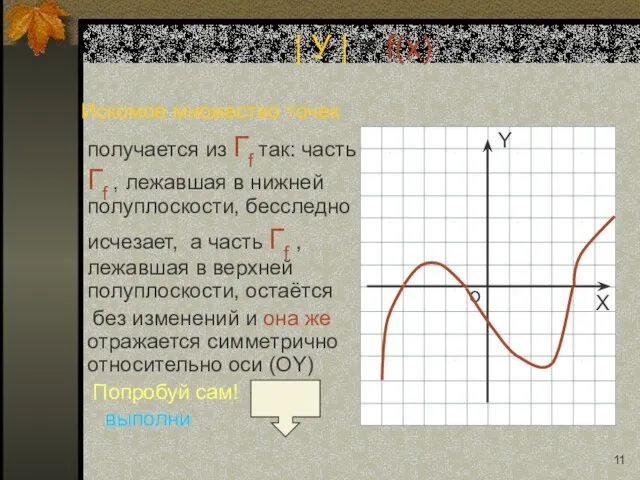
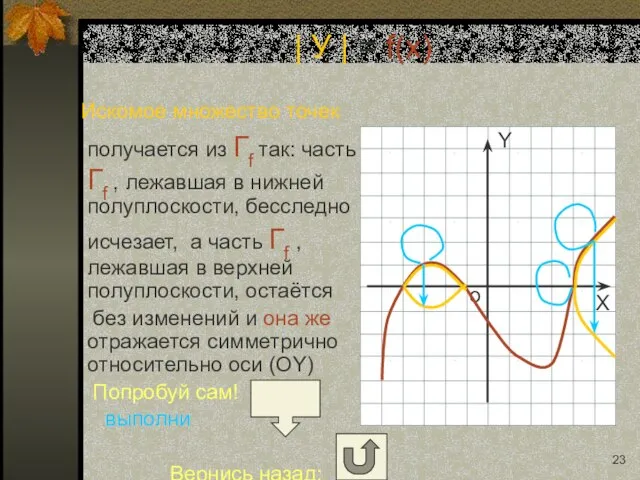
- 11. Искомое множество точек получается из Гf так: часть Гf , лежавшая в нижней полуплоскости, бесследно исчезает,
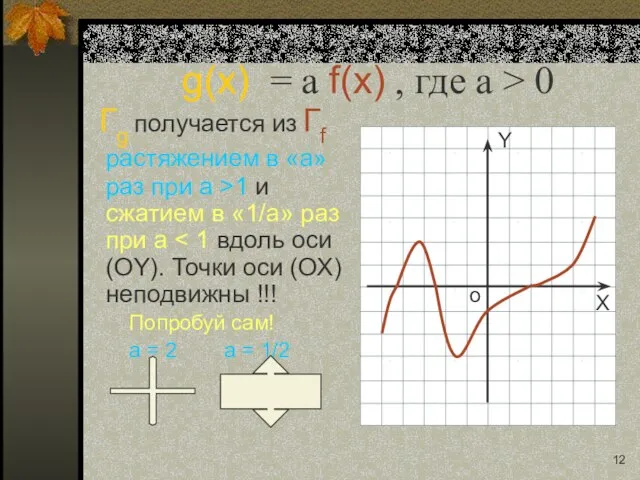
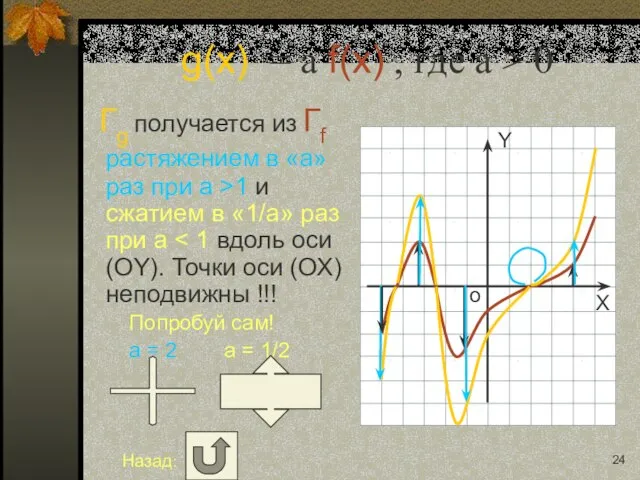
- 12. g(x) = a f(x) , где a > 0 Гg получается из Гf растяжением в «a»
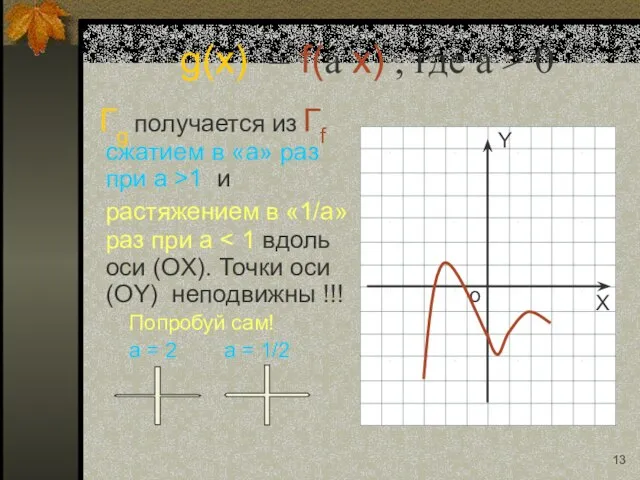
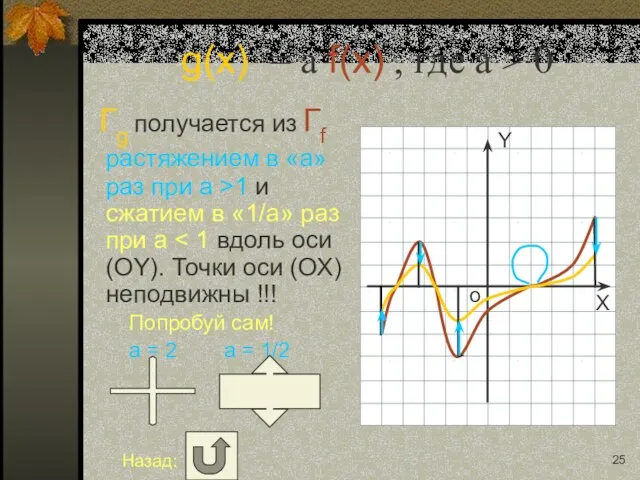
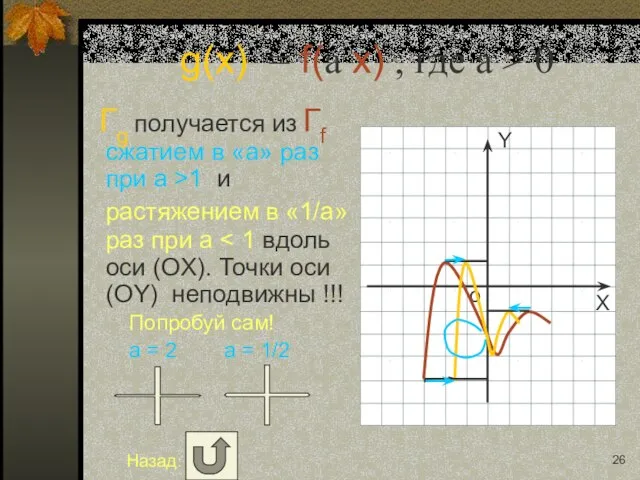
- 13. g(x) = f(a x) , где a > 0 Гg получается из Гf сжатием в «a»
- 14. Счастливо упражняться !!!
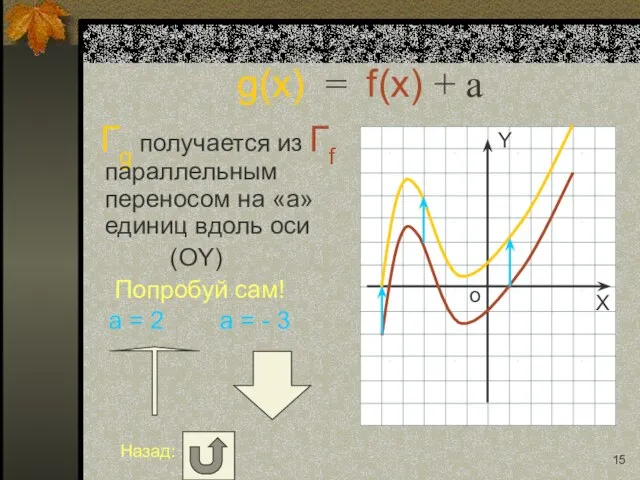
- 15. g(x) = f(x) + a Гg получается из Гf параллельным переносом на «a» единиц вдоль оси
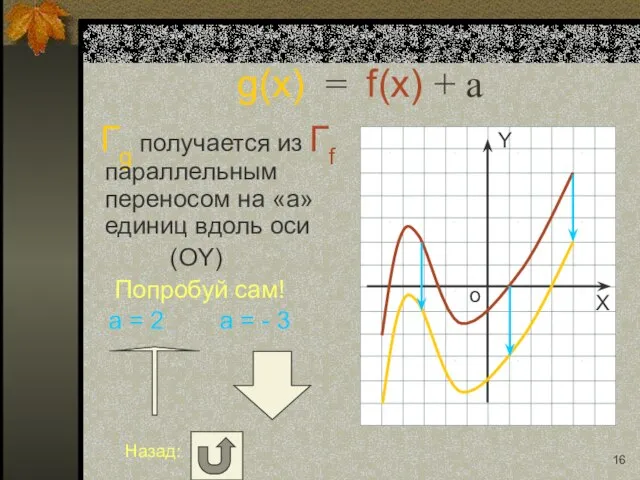
- 16. g(x) = f(x) + a Гg получается из Гf параллельным переносом на «a» единиц вдоль оси
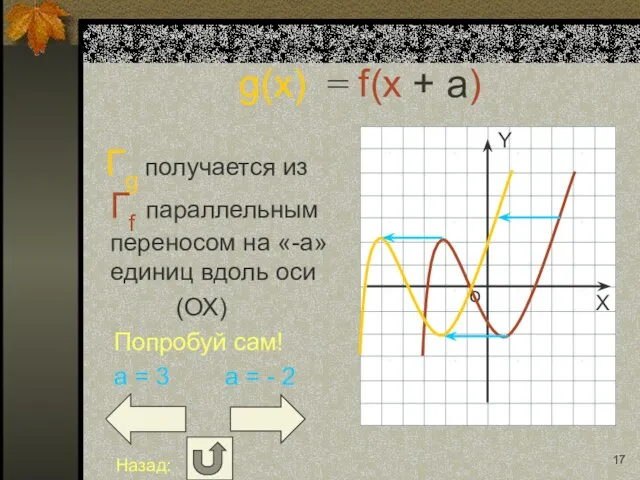
- 17. g(x) = f(x + a) Гg получается из Гf параллельным переносом на «-a» единиц вдоль оси
- 18. g(x) = f(x + a) Гg получается из Гf параллельным переносом на «-a» единиц вдоль оси
- 19. g(x) = - f(x) Гg получается из Гf симметрией относительно оси (ОХ) Попробуй сам! выполни Вернись
- 20. g(x) = f(-x) Гg получается из Гf симметрией относительно оси (OY) Попробуй сам! выполни Вернись назад:
- 21. Гg получается из Гf так: Часть Гf , лежавшая в верхней полуплоскости, остаётся без изменений, а
- 22. Гg получается из Гf так: Часть Гf , лежавшая в левой полуплоскости, бесследно исчезает, а часть
- 23. Искомое множество точек получается из Гf так: часть Гf , лежавшая в нижней полуплоскости, бесследно исчезает,
- 24. g(x) = a f(x) , где a > 0 Гg получается из Гf растяжением в «a»
- 25. g(x) = a f(x) , где a > 0 Гg получается из Гf растяжением в «a»
- 26. g(x) = f(a x) , где a > 0 Гg получается из Гf сжатием в «a»
- 28. Скачать презентацию




 Презентация на тему Геометрическая прогрессия и ее свойство
Презентация на тему Геометрическая прогрессия и ее свойство  Трикутники
Трикутники Перпендикуляр и наклонная к плоскости. Решение задач
Перпендикуляр и наклонная к плоскости. Решение задач Презентация на тему Иррациональные числа (8 класс)
Презентация на тему Иррациональные числа (8 класс)  Тригонометрия. Математическая игра АС-11
Тригонометрия. Математическая игра АС-11 Презентация на тему Сдвиг графика функции y = x вдоль осей координат
Презентация на тему Сдвиг графика функции y = x вдоль осей координат  Отображение. Отражение относительно прямой. Преобразование единичного квадрата
Отображение. Отражение относительно прямой. Преобразование единичного квадрата Решение задач
Решение задач Старинные меры массы и длины
Старинные меры массы и длины Скалярное произведение векторов
Скалярное произведение векторов Волшебный треугольник
Волшебный треугольник Тела вращения
Тела вращения Равнобедренный треугольник
Равнобедренный треугольник Пифагор и литература
Пифагор и литература Решение примеров и простых задач в пределах 10
Решение примеров и простых задач в пределах 10 Заниматика. Миром управляют числа
Заниматика. Миром управляют числа Случайные процессы с дискретными состояниями
Случайные процессы с дискретными состояниями Параллельные прямые
Параллельные прямые Lecture 6. Techniques of Integration (part 1)
Lecture 6. Techniques of Integration (part 1) Аналитическая панель
Аналитическая панель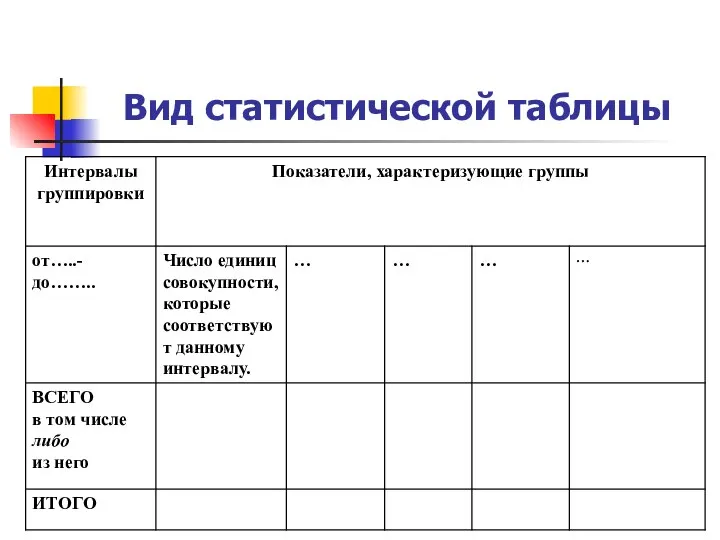 Вид статистической таблицы
Вид статистической таблицы Случаи сложения вида +7
Случаи сложения вида +7 Усеченная пирамида
Усеченная пирамида График равномерного движения
График равномерного движения Задачи на проценты. Схемы
Задачи на проценты. Схемы Многогранники в нашей жизни
Многогранники в нашей жизни Прямоугольный параллелепипед. Урок обобщения и систематизации знаний
Прямоугольный параллелепипед. Урок обобщения и систематизации знаний Презентация на тему Комбинации шара с многогранниками и фигурами вращения
Презентация на тему Комбинации шара с многогранниками и фигурами вращения