Многомерные случайные величины

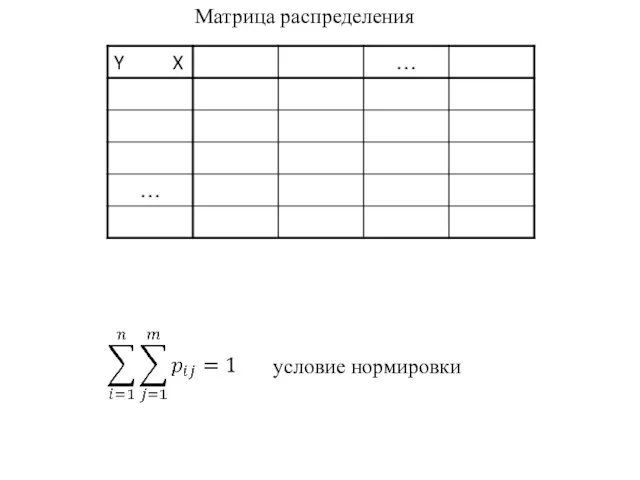
Матрица распределения
условие нормировки

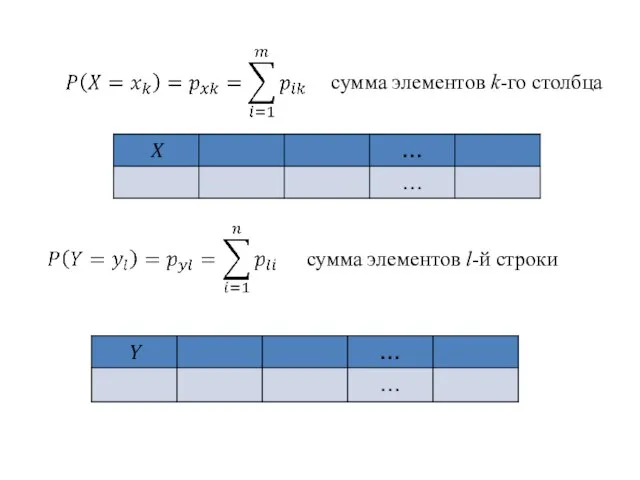
сумма элементов k-го столбца
сумма элементов l-й строки

Функция распределения системы непрерывных случайных величин

Вероятность невозможных событий
Вероятность достоверного события

Плотность распределения вероятностей системы непрерывных случайных величин

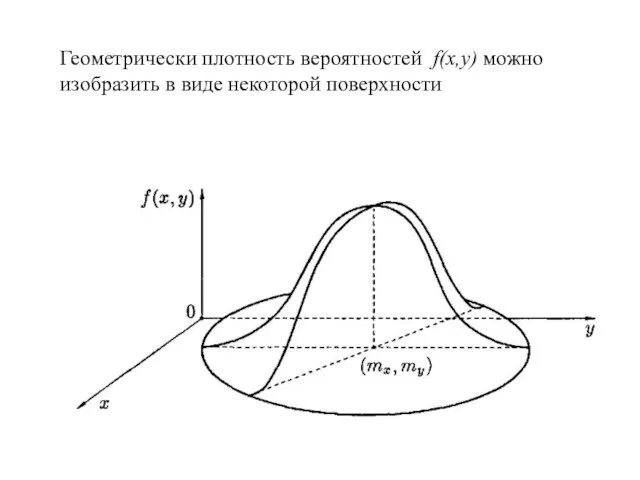
Геометрически плотность вероятностей f(x,y) можно изобразить в виде некоторой поверхности

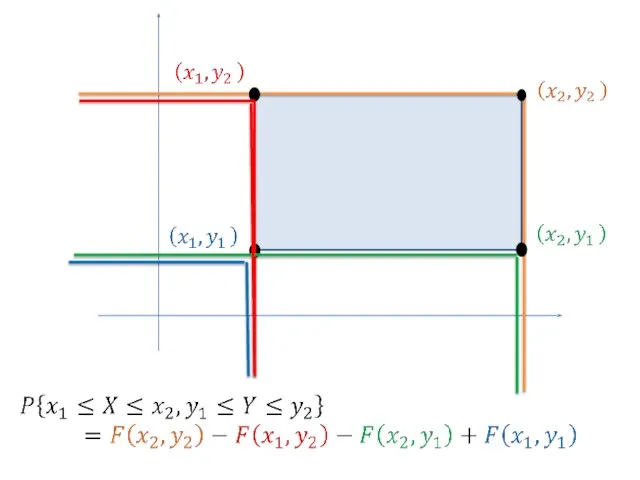
Вероятность попадания случайной точки (X,Y) в прямоугольник D со сторонами параллельными осям координат

Законы распределения отдельных величин входящих в систему. Условные законы распределения.

Определение. Условным законом распределения случайной величины X входящей в систему (X,Y) называется ее закон распределения вычисленный при условии, что другая случайная величина Y приняла определенное значение y .

Пример 2. Система случайных величин L и P представляет собой длину и вес осколка снаряда .

Числовые характеристики системы двух случайных величин

Теорема. Если случайные величины независимы, то их коэффициент корреляции равен нулю
Эквивалентно ли понятие некоррелированности случайных величин их независимости ???
Пример 1. Плотность распределения случайных величин (X,Y) выражается формулой
Найти ковариацию.

Пример 2 Вес и рост человека связаны положительной
корреляцией.
Пример 3. Производится два выстрела по цели; точка попадания первого выстрела регистрируется, и в прицел вводится поправка, пропорциональная ошибке первого выстрела с обратным знаком. Координаты точек попадания первого и второго выстрелов будут связаны отрицательной корреляцией.

Функции регрессии

Функции двух случайных величин
Математическое ожидание функции нескольких случайных величин

Свойства математического ожидания

Свойства дисперсии
3. Для любых случайных величин, имеющих конечную дисперсию, справедливо соотношение

4. Для любых случайных величин X иY, имеющих конечную дисперсию, справедливо соотношение
Пример. Найти математическое ожидание и дисперсию случайной величины X распределенной по биномиальному закону.

Свойства коэффициента корреляции
Замечания к разделу свойства дисперсии

Характеристическая функция

Пример 1. Характеристическая функция пуассоновской случайной величины.

Пример 2. Характеристическая функция гауссовской случайной величины.
Пример 3. Характеристическая функция случайной величины c равномерным распределением.

Свойства характеристической функции

Пример 1. M и N независимые пуассоновские случайные величины
2. Характеристическая функция суммы двух независимых случайных величин Z=X+Y

Пример 2. X и Y независимые гауссовские случайные величины

Пример . Пуассоновская случайная величина