Reshenie_sistem_logicheskikh_uravneniy_vse_metody

Будем придерживаться следующих обозначений:
дизъюнкция (+), конъюнкция (∙),
импликация (→), эквивалентность (≡), отрицание (¬).
На рисунках темный кружок обозначает 1, а светлый кружок – 0
F1 – количество решений при X1, равном 1
F0 – количество решений при X1, равном 0
N – число переменных в системе
уравнений.
F(N) = F1(N) + F0(N) – общее число решений.

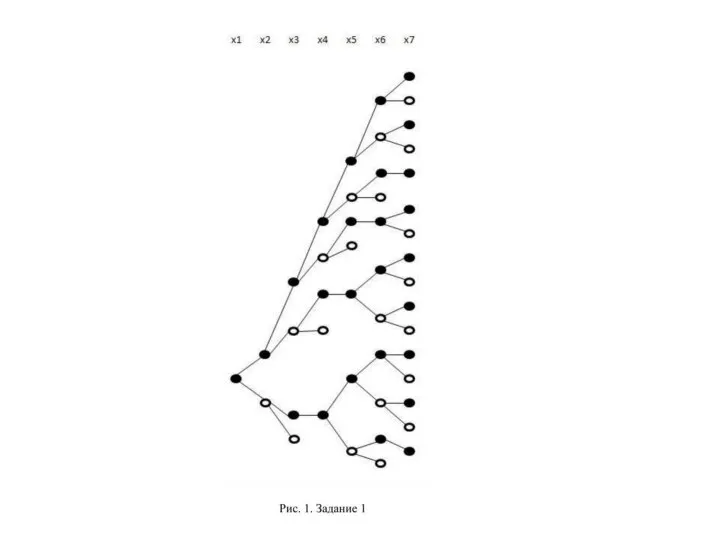
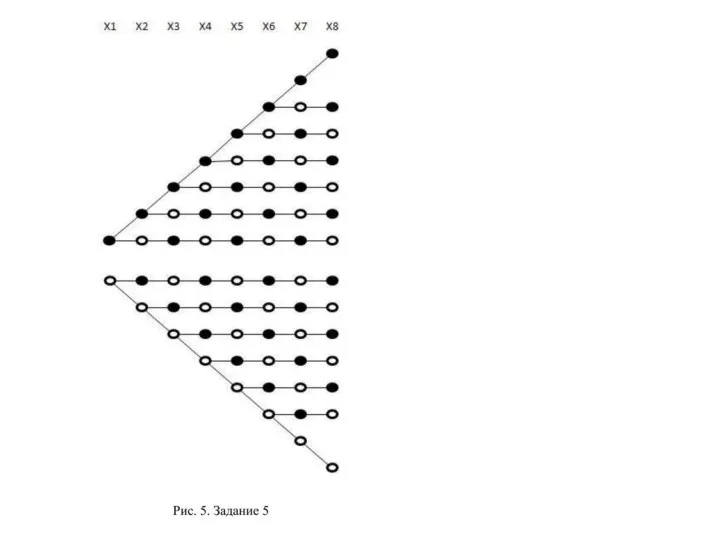
Задание 1
Найти количество решений системы уравнений
X1+X2∙X3=1
X2+X3∙X4=1
. . . . .
X7+X8∙X9=1
Построение дерева решений

Вначале полагаем X1 = 1. Тогда для первого уравнения значения X2 и X3 могут быть любыми. Таким образом, дерево построено до третьего уровня. Далее с учетом X2 и X3 выбираем X4. После этого алгоритм повторяется для каждой тройки переменных (см. рис. 1).
Начиная с четвертого уровня можно заметить, что F1(4)=F1(3)+F1(1), F1(5)=F1(4)+F1(2). Таким образом, получаем
F1(N) = F1(N-1) + F1(N-3) (1)

Из уравнения (1) получаем,
что F1(8) = 16 + 7 = 23, F1(9) = 23 + 11 = 34.
Для того чтобы построить дерево из нуля, можно воспользоваться нижней ветвью из Рис. 1.
Легко видеть, что она повторяет основное дерево, но со сдвигом вправо на 2. То есть F0(9) = F1(7) = 16.
Итого, F(9) = F1(9) + F0(9) = 34 + 16 = 50.

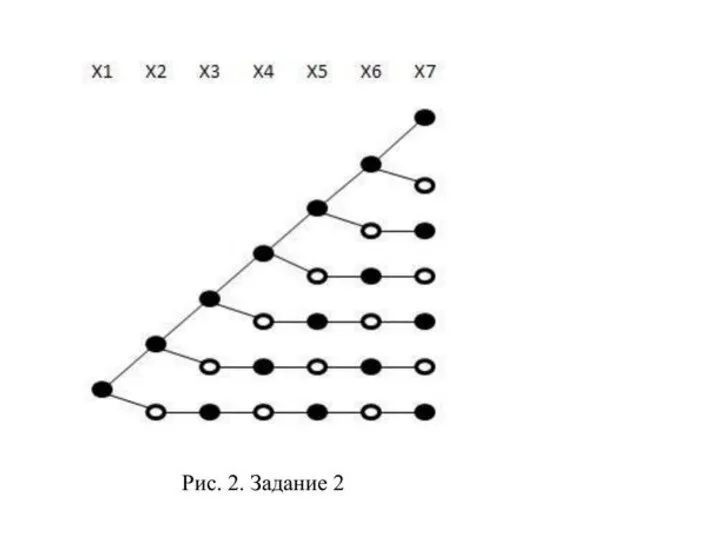
Для получения числа решений этого задания можно было не строить дерево решений полностью (см. рис. 2), так как очевидно, что F1(N) = N. Аналогично, F0(N) = N. Итого F(7) = 7 + 7 = 14.

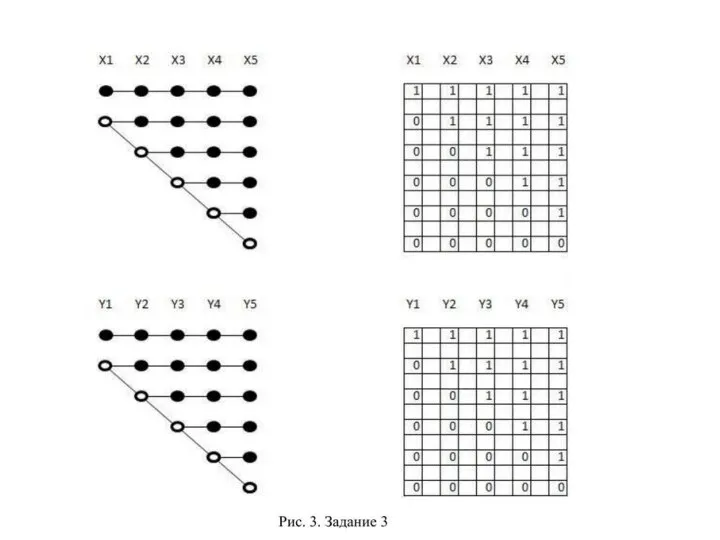
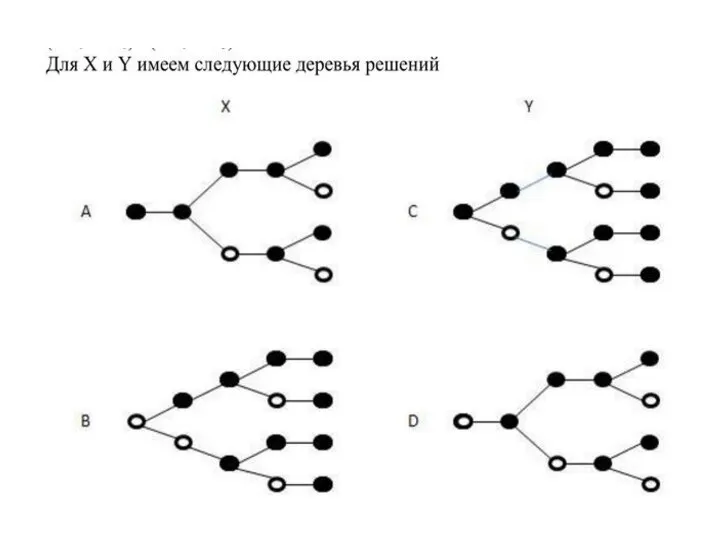
На рисунке 3 показаны деревья решений для X и Y и приведены соответствующие таблицы истинности.

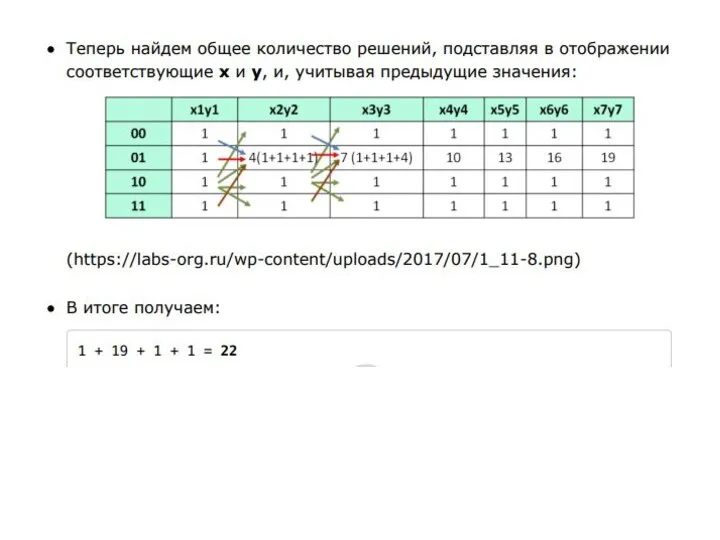
Из первых двух уравнений, поскольку X и Y независимы, следует, что общее число решений F(5) = 6 * 6 = 36.
Для того чтобы учесть третье уравнение, нужно для каждой переменной Y подсчитать какое число наборов из таблицы X не удовлетворяет уравнению. Импликация Yi → Xi = 0, если Yi = 1, а Xi = 0. То есть для Y1 = 1 третьему уравнению не удовлетворяют все строки из таблицы X, где X1 = 0. Число таких строк равно пяти. Для Y2 = 1 таких строк – 4 и т.д. Общее число строк, которые не удовлетворяют третьему уравнению равно 5 + 4 + 3 + 2 + 1 = 15.
Таким образом, общее число допустимых решений равно 36 – 15 = 21.

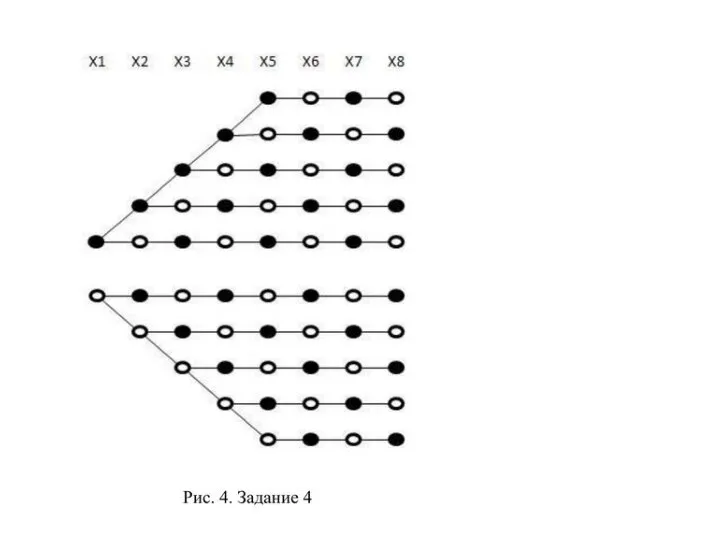
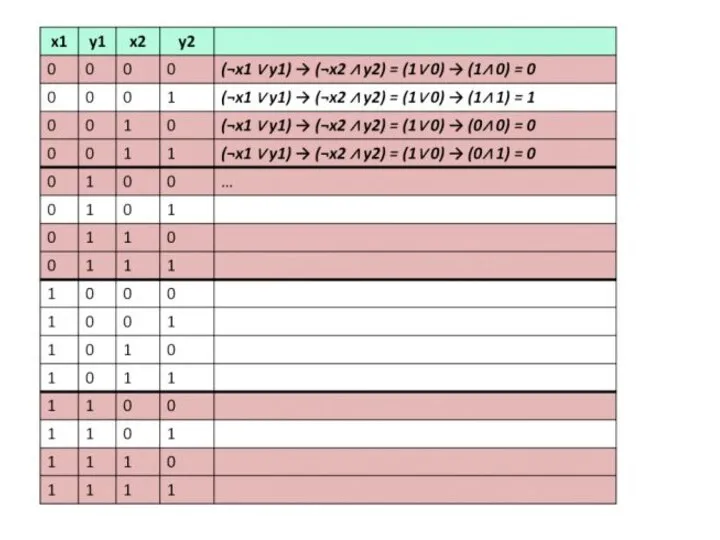
Для данного примера сложно определить конечную формулу F(N), проще построить дерево решений до конца (или хотя бы до X6). На рисунке 4 показано построенное дерево решений.
В результате получаем
F(8) = F1(8) + F0(8) = 5 + 5 = 10

Для этого примера, так же как и для предыдущего, проще построить дерево решений до конца (рис. 5).
В результате получаем
F(8) = F1(8) + F0(8) = 7 + 7 = 14

Метод битовых цепочек
(битовых масок)

1.

Ответ: 324
Ответ: 81

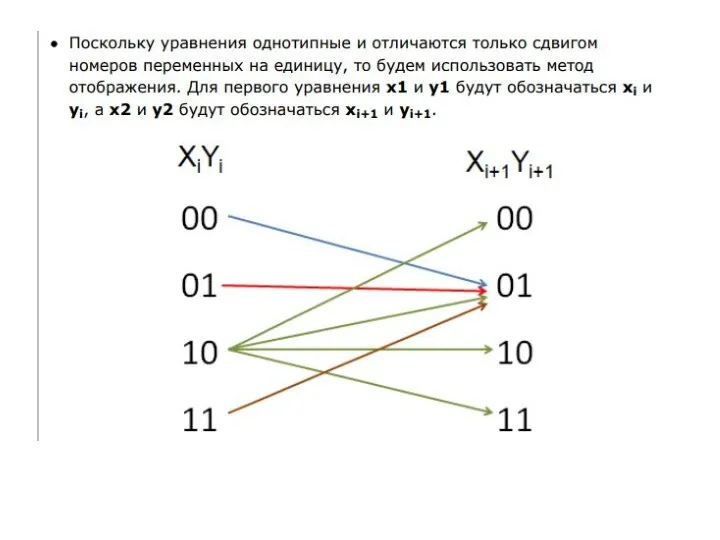
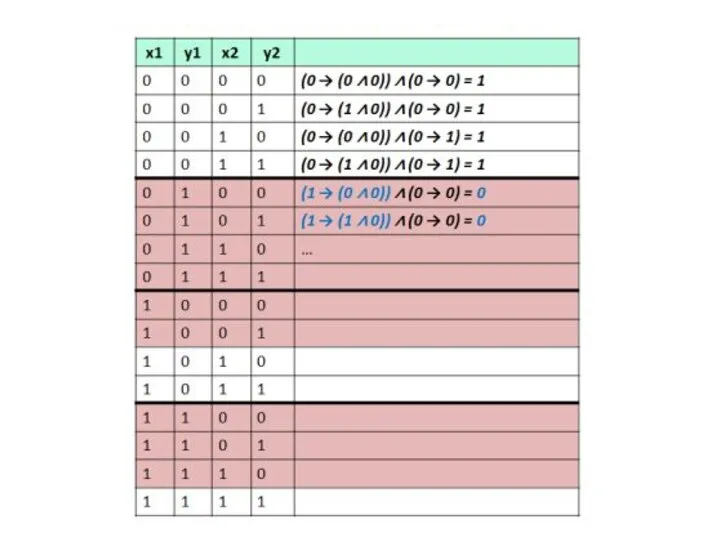
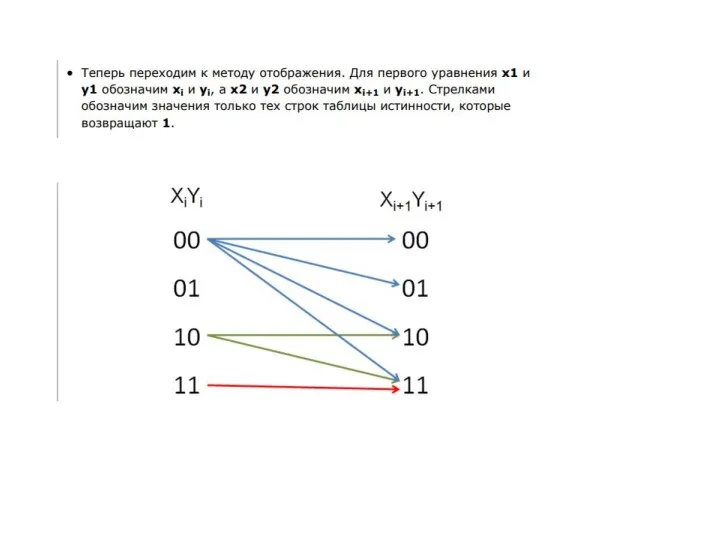
Метод отображений

4.