Множества и операции над ними. Пустое множество. Способы задания множеств. Подмножества данного множества
Содержание
- 2. Цель урока: Формировать знания учащихся о множествах и его элементах, о пустом множестве, о способах задания
- 3. Понятия теории множеств Понятие множества является одним из наиболее общих и наиболее важных математических понятий. Оно
- 4. Например: Множество цифр: 0;1;2;3;4;5;6;7;8;9 Множество букв русского алфавита Например: 1). Цифра 6 – элемент множества цифр.
- 5. Для обозначения множеств используют большие буквы латинского алфавита или фигурные скобки, внутри которых записывают элементы множества(при
- 6. Для обозначения элементов множества используют малые буквы латинского алфавита Например: 1). f = 6 – элемент
- 7. Множество может быть: 1). Конечное : Например: А— множество цифр 2). Бесконечное: Например: N – множество
- 8. На диаграмме Эйлера-Венна утверждение "множество А является подмножеством множество В" изображают так Если множество В состоит
- 9. СПОСОБЫ ЗАДАНИЯ МНОЖЕСТВ Перечислением элементов множества; Описанием общего (характеристического) свойства, объединяющего элементы. Например: 1). К =
- 10. Множества называются РАВНЫМИ, если они состоят из одних и тех же элементов Например: 1). Равными являются
- 11. Решение задач 1.Задайте перечислением элементов множества: а) А—множество гласных букв русского алфавита. Решение А = {а,
- 12. 2. Перечислить элементы следующих множеств: а) А= {х : хє ученикам вашего класса, которые сейчас отсутствуют
- 13. 3. Какие из следующих множеств являются пустыми? неверно множество решений уравнений х²-4=0 множество решений уравнений х=х+2
- 14. 5. Даны множества: а) множество А всех трапеций. б) множество В всех прямоугольников. в) множество С
- 15. Суммой, или объединением произвольного конечного или бесконечного множества множеств называется множество, состоящее из тех и только
- 16. ОБЪЕДИНЕНИЕ МНОЖЕСТВ А и В Например: L= { 5;7;9;3;1}, W= { 1;0;8;2;4;5;6 } => LUW={0;1;2;3;4;5;6;7;8;9} С
- 17. Пересечением любого конечного или бесконечного множества множеств называется множество, состоящее из тех и только тех элементов,
- 18. ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ А и В С= А ∩ В К ∩ М = ø Например: L=
- 19. Разностью между множеством В и множеством А называется множество всех элементов из В , не являющихся
- 20. РАЗНОСТЬ МНОЖЕСТВ А и В Решение задач: 1. Дано: M = { a;b;c;d } , N
- 21. Дополнением множества А называется множество, состоящее из всех элементов, не принадлежащих множеству А (но принадлежащих универсальному
- 22. Задача. Каждый учащийся в классе изучает английский или французский язык. Английский язык изучают 25 учащихся, французский
- 23. Подведение итогов урока: Приведите примеры множеств. Какие бывают множества по количеству элементов? Как обозначаются множества? Как
- 25. Скачать презентацию





















 Применение производной к исследованию функции
Применение производной к исследованию функции Мир многогранников
Мир многогранников Синус, косинус и тангенс острого угла прямоугольного треугольника. 8 класс
Синус, косинус и тангенс острого угла прямоугольного треугольника. 8 класс Презентация на тему Симметрия в нашей жизни
Презентация на тему Симметрия в нашей жизни  Путешествие в город Дробей на проспект Умножения. 6 класс
Путешествие в город Дробей на проспект Умножения. 6 класс Непрерывность функции на отрезке
Непрерывность функции на отрезке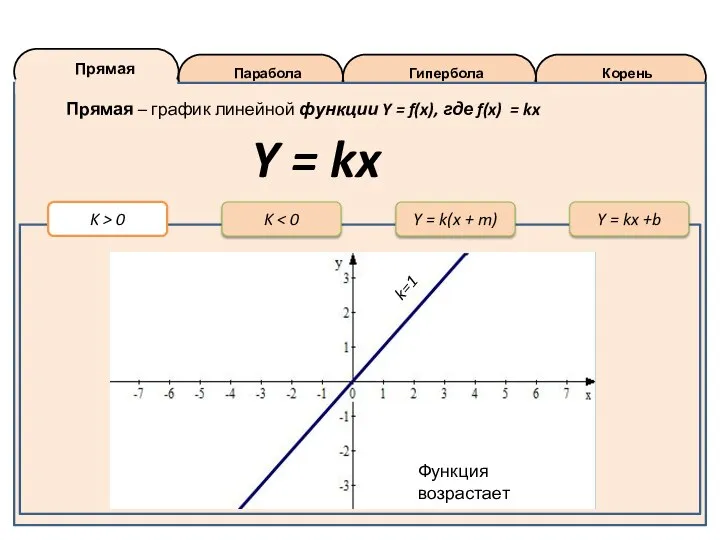 Прямая. Парабола. Гипербола. Корень
Прямая. Парабола. Гипербола. Корень Логарифмические неравенства
Логарифмические неравенства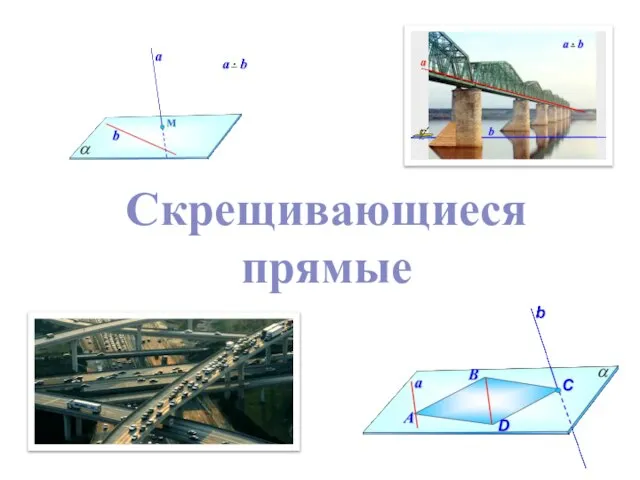 Скрещивающиеся прямые
Скрещивающиеся прямые Чертежи к уроку Вертикальные углы
Чертежи к уроку Вертикальные углы Синус, косинус, тангенс и котангенс угла
Синус, косинус, тангенс и котангенс угла Национальный стандарт по библиотечной статистике: преемственность и новые подходы
Национальный стандарт по библиотечной статистике: преемственность и новые подходы Тригонометрические и Логарифмические уравнения. Объёмы тел
Тригонометрические и Логарифмические уравнения. Объёмы тел Теория вероятностей. Действия над вероятностями
Теория вероятностей. Действия над вероятностями Определите, какими являются данные величины: прямо пропорциональными, обратно пропорциональными или ни теми ни другими
Определите, какими являются данные величины: прямо пропорциональными, обратно пропорциональными или ни теми ни другими Сложение и вычитание многозначных чисел
Сложение и вычитание многозначных чисел Заряди мозги! По материалам книги: Математика в логических упражнениях Гайштут А.Г
Заряди мозги! По материалам книги: Математика в логических упражнениях Гайштут А.Г Презентация на тему Многочлены
Презентация на тему Многочлены  Показательная функция, ее свойства и график
Показательная функция, ее свойства и график Метод математической индукции
Метод математической индукции Функції. Графік функції. 7 клас
Функції. Графік функції. 7 клас Решение уравнений (часть 2)
Решение уравнений (часть 2) Построение сечений тетраэдра
Построение сечений тетраэдра Решение задачи Корабли или история 7 семестров
Решение задачи Корабли или история 7 семестров Построение сечений в тетраэдре
Построение сечений в тетраэдре Решение задач
Решение задач Математическая статистика, комбинаторика
Математическая статистика, комбинаторика Четырехугольники
Четырехугольники