Содержание
- 2. Что называется векторным произведением?
- 3. Обозначение: Геометрически векторное произведение есть ориентированная площадь параллелограмма, построенного на векторах ,представленная псевдовектором, ортогональным этому параллелограмму.
- 4. Свойства векторного произведения: При перестановке сомножителей векторное произведение меняет знак (антикоммутативность), т.е Векторное произведение обладает сочетательным
- 5. Пример: Найти векторное произведение векторов, заданных своими координатами: a (2;1;-3) и b (0;-1;1)
- 6. С помощью векторов можно найти S треугольника, но как? Сейчас покажу Есть формула для вычисления площади
- 7. Пример: Даны три точки: Найти площадь треугольника ABC. Найдем координаты этих векторов: И вычислим площадь: Площадь
- 8. Так же можно найти площадь параллелограмма: Вычислите площадь параллелограмма, построенного на векторах a=(1;-2;5) и b(0;-2;1). Решение.
- 9. Всё легко и просто, учитесь ребята!!!
- 12. Скачать презентацию









 Морской бой
Морской бой Преобразование целого выражения в многочлен
Преобразование целого выражения в многочлен Таблица умножения
Таблица умножения Pervoobraznaya
Pervoobraznaya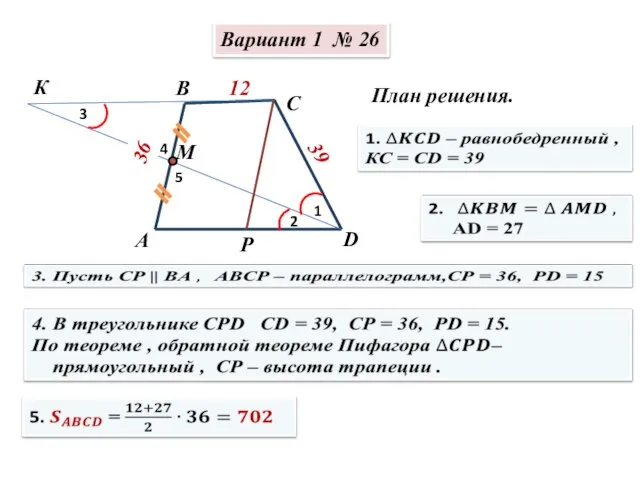 Сборник И.В. Ященко. Решение заданий №26
Сборник И.В. Ященко. Решение заданий №26 Решение задач на применение признаков подобия треугольников
Решение задач на применение признаков подобия треугольников 1ce713f2e27cb837f4d7376560237c07
1ce713f2e27cb837f4d7376560237c07 Парадокс раздела ставки
Парадокс раздела ставки Теорема Пифагора
Теорема Пифагора Математика ЕГЭ. Треугольники
Математика ЕГЭ. Треугольники Объемы многогранников и тел вращения. Устная работа
Объемы многогранников и тел вращения. Устная работа Сложнние и вычитание алгебраических дробей с одинаковыми знаменателями
Сложнние и вычитание алгебраических дробей с одинаковыми знаменателями Иррациональные неравенства и способы их решения
Иррациональные неравенства и способы их решения Компетентность
Компетентность Логические задачи. 1 класс
Логические задачи. 1 класс Перпендикуляр и наклонная. Угол между прямой и плоскостью
Перпендикуляр и наклонная. Угол между прямой и плоскостью Теорема Фалеса
Теорема Фалеса Умники и умницы. Викторина по математике
Умники и умницы. Викторина по математике Занимательные задачи
Занимательные задачи Лингвистика в математике
Лингвистика в математике Нахождение площади фигур и объемов тел
Нахождение площади фигур и объемов тел Второй признак подобия треугольников
Второй признак подобия треугольников Симплекс-решетчатое планирование. Диаграммы состав-свойство Шеффе. Тема 8
Симплекс-решетчатое планирование. Диаграммы состав-свойство Шеффе. Тема 8 L_3_U
L_3_U Повторение курса 5 класса
Повторение курса 5 класса Задачи с дробями
Задачи с дробями Математический тренажёр. Устные упражнения на уроках математики в 7 классе как один из способов отработки навыка устного счёта
Математический тренажёр. Устные упражнения на уроках математики в 7 классе как один из способов отработки навыка устного счёта Решение задач с помощью геометрии
Решение задач с помощью геометрии