Наука эконометрика

Эконометрика — наука, изучающая количественные и качественные экономические (социально-экономические) взаимосвязи с помощью математических и статистических методов и моделей.

На первом этапе устанавливается причинно-следственная связь между признаками, которая основывается на знании закономерностей изучаемого явления и заключается в подборе факторных и результа­тивных признаков, между которыми существует взаимосвязь.
Этапы:

На втором этапе задача состоит в определении формы связи и вы­боре математического уравнения, которое могло бы наиболее полно отразить характер взаимосвязи между изучаемыми признаками.

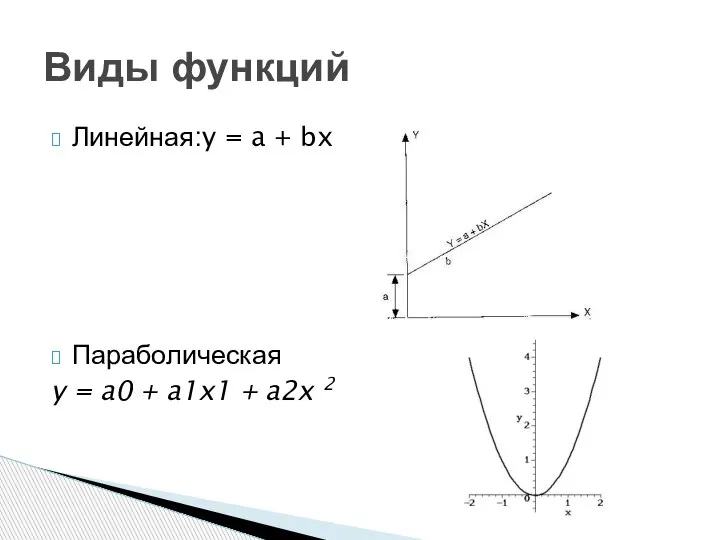
Линейная:y = a + bx
Параболическая
y = a0 + a1x1 + a2x 2
Виды функций

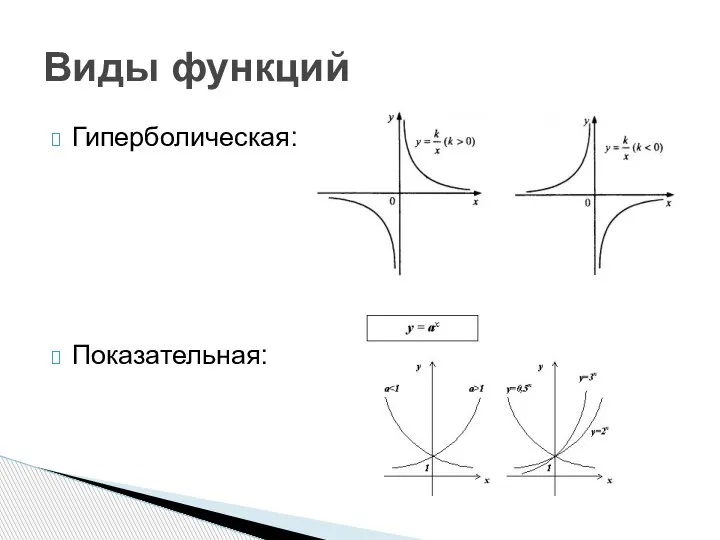
Гиперболическая:
Показательная:
Виды функций

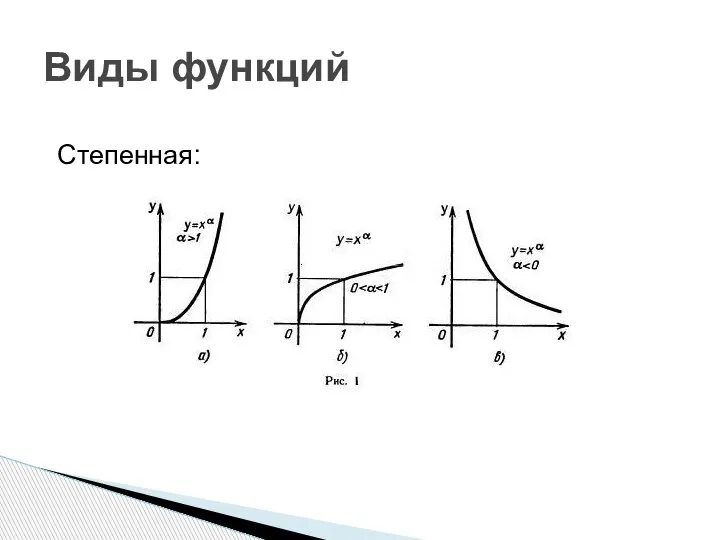
Виды функций
Степенная:

Метод наименьших квадратов (МНК, англ. OrdinaryLeastSquares, OLS) — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных.

Верная формула функции всегда будет давать минимальное отклонение фактических значений результирующего показателя от теоретических

Приравняем к нулю частные производные a и b, затем разделим на n оба уравнения
где n — объем исследуемой совокупности (число единиц наблюдения)

На третьем этапе рассчитываются параметры уравнения связи. Па­раметр а, как правило, экономического смысла не имеет.
Параметр b называется коэффициентом регрессии - показывает, на сколько еди­ниц изменяется значение результативного признака при изменении значения факторного признака на единицу. Знак при коэффициенте регрессии показывает направление связи.

Пример линейной функции (парная регрессия)

На четвертом этапе определяется теснота связи, коэффициент детерминации, ошибка апроксимации.

Линейный коэффициент корреляции
Изменяется [-1;+1]. В зависимости от величины коэффициента корреляции делают выводы о тесноте связи. В экономических исследованиях используется примерно следующая градация:
0
0,2
0,5
0,75
0,95

Значимость линейного коэффициента корреляции проверяется на основе t-критерий Стьюдента.
Расчетное значение t-критерия сравнивается с его табличным, определяемым по таблице табулированных значений:
где — уровень значимости, который показывает вероятность принятия ошибочного решения; — число степеней свободы, характеризует количество свободно варьируемых элементов совокупности (количество наблюдений).

Если расчетное значение t-критерия по модулю превышает табличное, то коэффициент корреляции признается значимым. Если расчетное значение t-критерия по модулю меньше критического, то гипотеза о равенстве коэффициента корреляции нулю принимается с вероятностью , и он признается незначимым, а, следовательно, не может быть использован для характеристики связи между изучаемыми признаками генеральной совокупности, так как единицы выборочной совокупности не отражают реальную структуру генеральной совокупности

Коэффициент детерминации
Коэффициент детерминации показывает, какая часть вариации результативного признака обусловлена вариацией факторного при­знака. Изменяется [0;+1].
Вторая формула: D = r2

Средняя ошибка аппроксимации - среднее отклонение расчетных значений от фактических: , где yx - расчетное значение по уравнению. Значение средней ошибки аппроксимации до 15% свидетельствует о хорошо подобранной модели уравнения.
Средняя ошибка апроксимации