Некоторые часто встречающиеся дискретные распределения

Стрелок производит 3 выстрела по мишени. Вероятность попадания при одном выстреле равна 0,6. Х-число попаданий. Найти распределение Х.
ПРИМЕР.

Найдем MX и DX для биномиального распределения
Введем для каждого i=1,2…n случайную величину Zi .
Тогда
Х= Z1 +Z2 +…+Zn

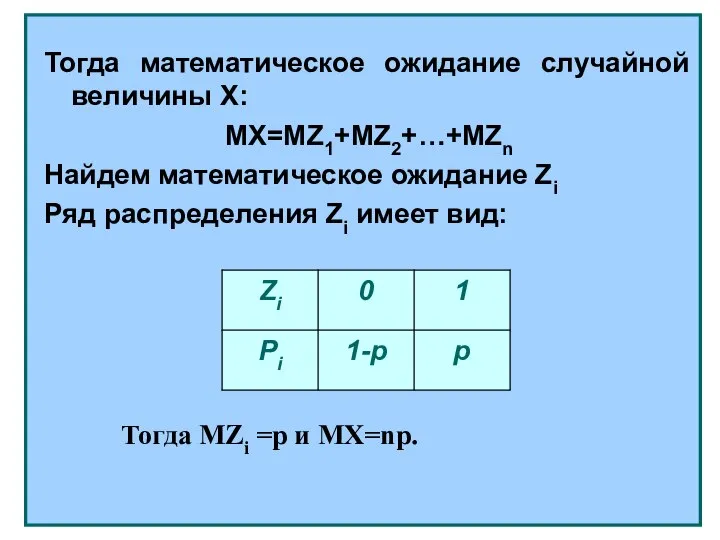
Тогда математическое ожидание случайной величины Х:
MX=MZ1+MZ2+…+MZn
Найдем математическое ожидание Zi
Ряд распределения Zi имеет вид:
Тогда MZi =p и MX=np.

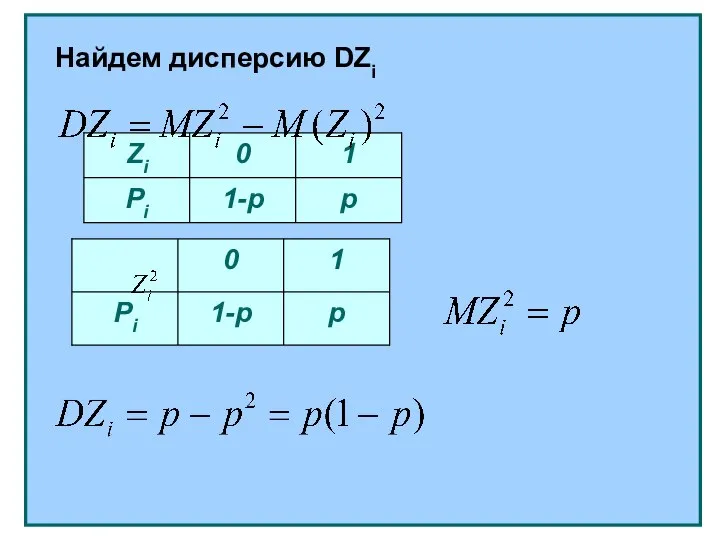
Найдем дисперсию DZi

Так как случайные величины Zi независимы, то

Таким образом, для случайной величины,
распределенной по биномиальному закону,

Распределение Пуассона
Пусть Х – число наступлений редкого события за
некоторый промежуток времени.
Известно среднее число наступлений этого
события за этот промежуток времени a
Тогда Х может принимать значения
0, 1, 2,…,k,…
Говорят, что Х имеет распределение Пуассона с параметром a.

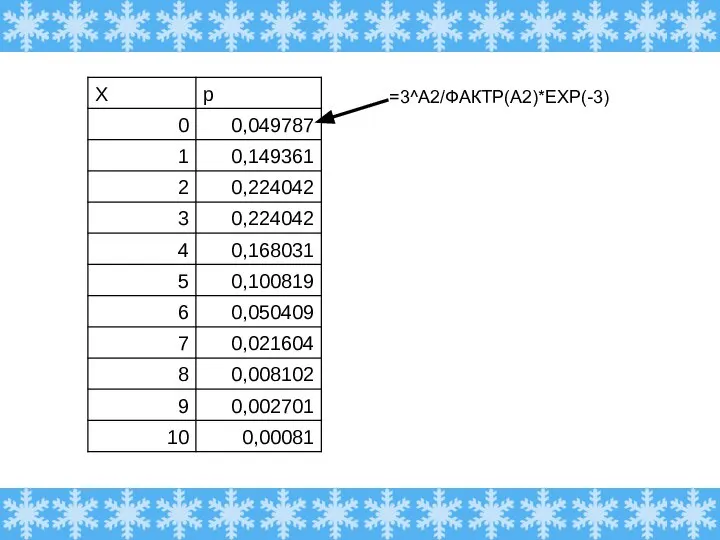
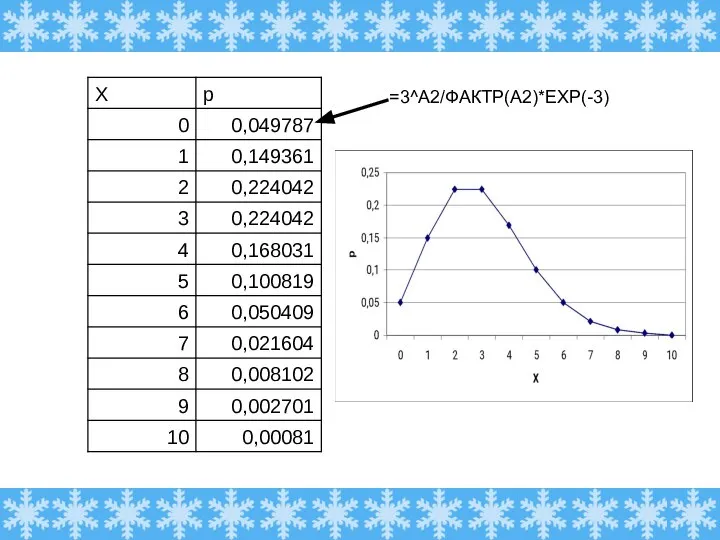
При работе оборудования время от времени
возникают сбои. В среднем за месяц возникает
3 сбоя. Пусть Х-число сбоев за месяц. Найти
распределение Х.
Вычислить вероятности событий:
А - за месяц будет не больше 2-х сбоев;
В - в течение месяца произойдет хотя бы один
сбой.
ПРИМЕР.

=3^A2/ФАКТР(A2)*EXP(-3)

=3^A2/ФАКТР(A2)*EXP(-3)

Для распределения Пуассона MX=a, DX=a

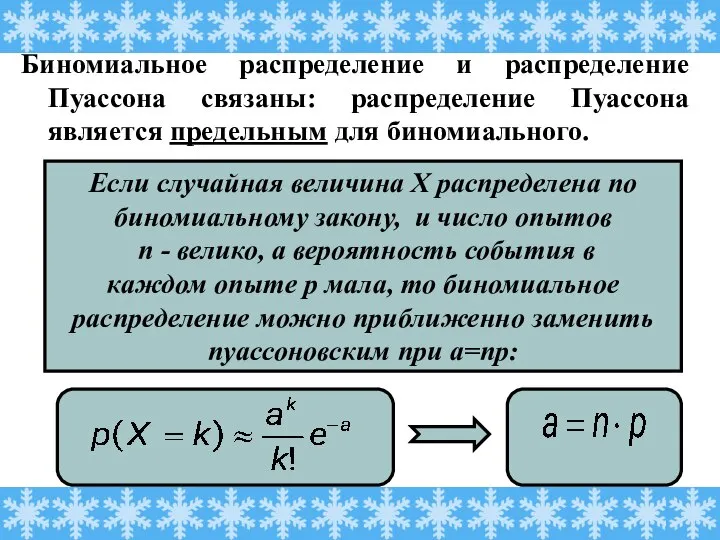
Биномиальное распределение и распределение Пуассона связаны: распределение Пуассона является предельным для биномиального.
Если случайная величина Х распределена по
биномиальному закону, и число опытов
n - велико, а вероятность события в
каждом опыте р мала, то биномиальное
распределение можно приближенно заменить
пуассоновским при a=np:

ПРИМЕР.
По цели производится 50 независимых
выстрелов. Вероятность попадания в цель
при одном выстреле равна 0.04.
Используя предельное свойство
биномиального распределения, найти
вероятность того, что в цель попадет
один снаряд.

Решение:
Найдем параметр a распределения Пуассона:
Событие А - попадание при одном выстреле.
Вероятность р(А)=0.04. Всего производится серия таких выстрелов: n=50.
Так как р достаточно мало, а n - велико, биномиальное распределение приближенно можно заменить распределением Пуассона.

Тогда вероятность р50(1) того, что из 50-ти выстрелов будет одно попадание по формуле Пуассона будет:

ГЕОМЕТРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ
Проводится n независимых испытаний,
в каждом из которых возможны 2 исхода: успех
с вероятностью p и неудача с вероятностью 1-p.
Испытания проводятся до первого успеха. Пусть X –
число проведенных испытаний. Тогда X имеет
геометрическое распределение.

ГЕОМЕТРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ
Х принимает значения 1,2,3…,k,…

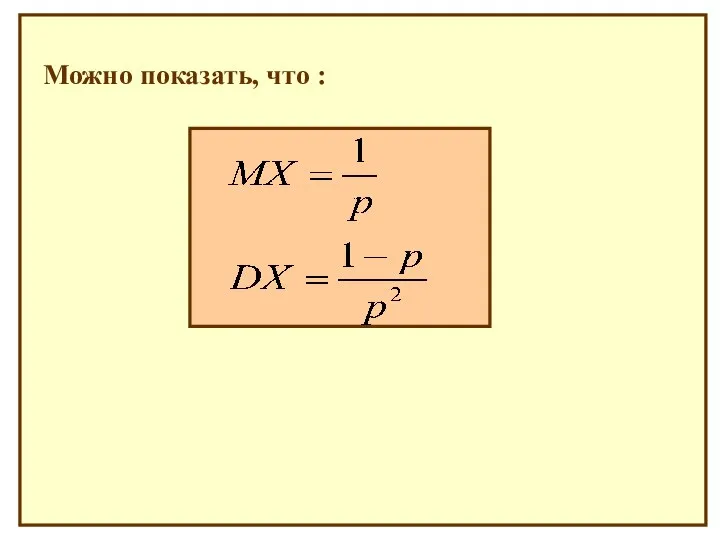
Можно показать, что :

Игральная кость бросается до первого появления
шестерки. Х- число сделанных бросков. Найти
распределение Х, MX, DX
ПРИМЕР.