Слайд 2Первообразной функцией по отношению к данной функции у = f(x) называется такая

функция F(x), производная от которой равна данной функции, т.е. F′(x) = f(x).
Для данной функции у = f(x) первообразных функций бесчисленное множество, т.к. любая из функций F(x) + С, также является первообразной для у = f(x).
Слайд 3 Совокупность всех первообразных
F(x) + С для данной функции у

= f(x) называется ее неопределенным интегралом обозначается символом:
где f(x)dx - называется подынтегральным выражением,
функция f(x) - подынтегральной функцией.
Слайд 4 Геометрический смысл неопределенного интеграла.
Геометрически, неопределенный интеграл представляет собой семейство интегральных

кривых на плоскости, полученных путем параллельного переноса графика функции
у = F(x) вдоль оси ординат (рис.3)
Слайд 5Основные свойства неопределённого интеграла
Свойство 1. Производная неопределенного интеграла равна подынтегральной функции:
Свойство 2.

Дифференциал неопределенного интеграла равен подынтегральному выражению:
Слайд 6Свойство 3. Интеграл от дифференциала функции равен этой функции плюс const:
Свойство 4.

Линейность интеграла.
Слайд 13 Непосредственное интегрирование – это метод, основанный на применении тождественных преобразований подынтегральной

функции, а также основных свойств неопределенного интеграла и табличных интегралов.
Слайд 14Непосредственное интегрирование
Наиболее часто используются следующие преобразования подынтегральной функции:
Деление числителя на знаменатель

почленно;
Применение формул сокращенного умножения;
Применение тригонометрических тождеств.
Слайд 15Пример № 1. Найти неопределенный интеграл методом непосредственного интегрирования.
Используя свойство неопределенного интеграла,

вынесем за знак интеграла постоянный множитель.
Затем, выполняя элементарные математические преобразования, приведем подынтегральную функцию к степенному виду:
Слайд 20Замена переменной
(метод подстановки)
Замена переменной (метод подстановки) – это метод, заключающийся во

введении новой переменной с целью преобразования данного интеграла в табличный.
Слайд 21Замена переменной
(метод подстановки)
Чаще всего этот метод используется, если в подынтегральном выражении

содержится сложная функция, тогда ее промежуточный аргумент и надо обозначить как новую переменную.
Слайд 22НАПРИМЕР
Далее необходимо выполнить следующие действия:
Найти дифференциал новой переменной ;
Записать прежний интеграл,

используя только переменную t, если подстановка сделана правильно, то полученный интеграл должен быть табличным;
используя таблицу интегралов, записать решение для подынтегральной функции ;
Осуществить обратную подстановку, заменив переменную t.
Слайд 23 Подстановка (замена переменной) в определённом интеграле - необходимо выполнить следующие действия:
Ввести

новую переменную t = t (x);
Найти дифференциал новой переменной dt = t′ (x)dx;
вычислить новые значения пределов интегрирования:
α = t (a) и β = t (b)
Записать прежний интеграл, используя только переменную t и новые пределы α и β;
Используя таблицу интегралов, записать решение для полученной подынтегральной функции;
Применив формулу Ньютона-Лейбница, вычислить значение определенного интеграла.
Замечание. При вычислении определённых интегралов с помощью подстановки нет необходимости возвращаться к первоначальному аргументу.
Слайд 24Пример № 5. Найти неопределенный интеграл, используя метод замены переменной.
Сделаем замену переменной

t = sin x, тогда
dt = (sin x)′dx = cos x dx.
Исходный интеграл имеет вид:
Таким образом, мы получили неопределенный интеграл табличного вида: степенная функция.
Используя правило нахождения неопределенного интеграла от степенной функции, найдем:
Слайд 25Сделав обратную замену, получим окончательный ответ:
Ответ:

Слайд 293. Метод интегрирования по частям
Метод интегрирования по частям – это метод, заключающийся

в использовании формулы:
Слайд 30Данный метод интегрирования основан на тождестве:
где u = f(x) и v =

φ(x) - две функции, имеющие на данном промежутке производные.
Взяв интеграл от обеих частей данного тождества, будем иметь:
































 Мера Лебега
Мера Лебега Задачи на проценты. Путешествие по лабиринту, урок-игра в 5-м классе
Задачи на проценты. Путешествие по лабиринту, урок-игра в 5-м классе Теория преобразования графиков функций
Теория преобразования графиков функций Цилиндр. Задачи
Цилиндр. Задачи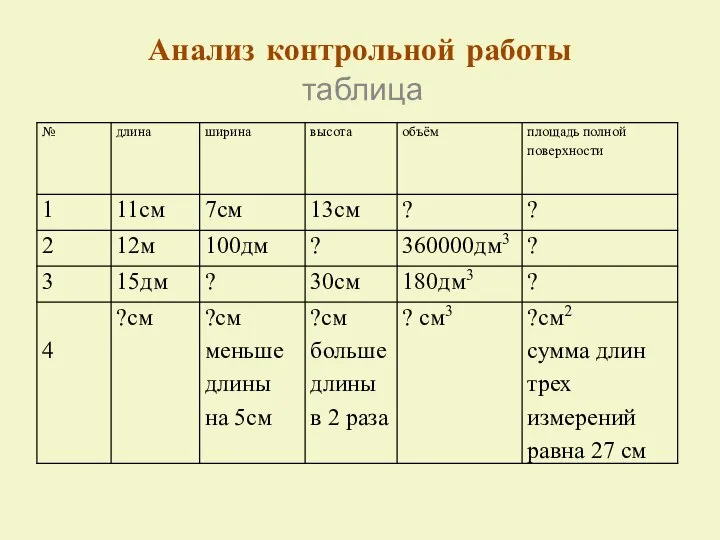 Таблицы и диаграммы. Чтение и составление таблиц
Таблицы и диаграммы. Чтение и составление таблиц Естественный отбор. Бинарный урок по биологии и математике (часть 3)
Естественный отбор. Бинарный урок по биологии и математике (часть 3) Перпендикулярные прямые
Перпендикулярные прямые Математическая игра «Звездный час»
Математическая игра «Звездный час» Математические ребусы (2 класс)
Математические ребусы (2 класс) Аналитические методы исследования дробнорациональных функций и построение их графиков с использованием программных средств
Аналитические методы исследования дробнорациональных функций и построение их графиков с использованием программных средств Практический расчёт, оценка и прикидка. Подготовка к ЕГЭ (1)
Практический расчёт, оценка и прикидка. Подготовка к ЕГЭ (1) Математическая грамотность (7 класс)
Математическая грамотность (7 класс) Погрешность результата измерения
Погрешность результата измерения Математика. Решение задач
Математика. Решение задач Свойство биссектрисы угла
Свойство биссектрисы угла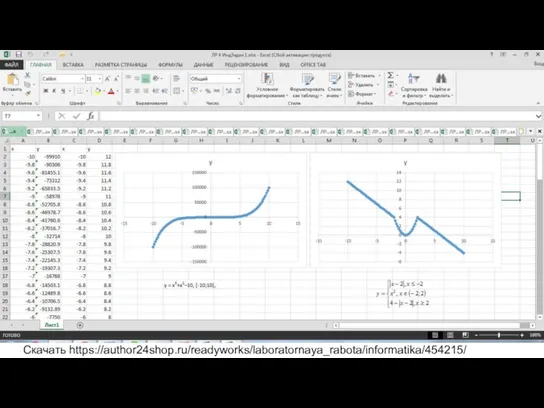 Постройте графики функций
Постройте графики функций Презентация на тему Вычисление объёма цилиндра
Презентация на тему Вычисление объёма цилиндра  Математика
Математика Работа по математике. Симметрия
Работа по математике. Симметрия Производная вокруг нас
Производная вокруг нас Периметр восьмиугольника
Периметр восьмиугольника 29.09 Решение задач
29.09 Решение задач Теория вероятностей и математическая статистика. Двумерные случайные величины. Лекция 8
Теория вероятностей и математическая статистика. Двумерные случайные величины. Лекция 8 Спин и расширенное супервремя
Спин и расширенное супервремя Виды треугольников. 5 класс
Виды треугольников. 5 класс Случаи сложения вида +5
Случаи сложения вида +5 Решение уравнения в 1классе
Решение уравнения в 1классе Эконометрика. Лекция 2
Эконометрика. Лекция 2