Содержание
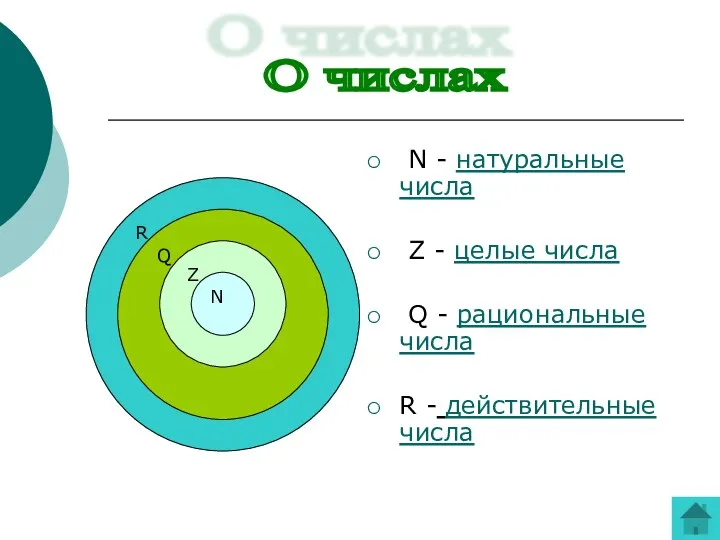
- 2. N - натуральные числа Z - целые числа Q - рациональные числа R - действительные числа
- 3. N - натуральные числа Числа 1, 2, 3, …, употребляемые при счете предметов, образуют множество натуральных
- 4. Целые числа Натуральные числа, противоположные им числа и число нуль составляют множество целых чисел. Обозначают буквой
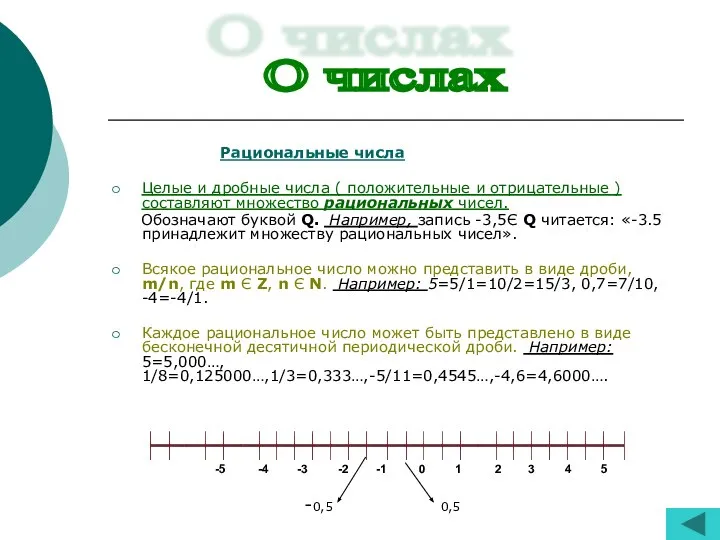
- 5. Рациональные числа Целые и дробные числа ( положительные и отрицательные ) составляют множество рациональных чисел. Обозначают
- 7. Скачать презентацию


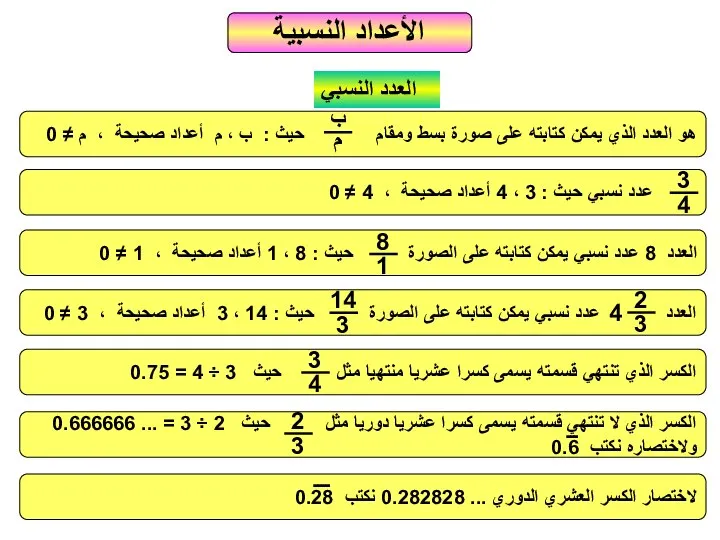 الأعداد انسبية
الأعداد انسبية Своя игра 3
Своя игра 3 Степінь з цілим показником
Степінь з цілим показником Интересные факты в математике
Интересные факты в математике Решение задач
Решение задач Предмет, методы и задачи статистики
Предмет, методы и задачи статистики Сложение и вычитание в пределах первого десятка
Сложение и вычитание в пределах первого десятка Математическое моделирование. Лекция 1
Математическое моделирование. Лекция 1 Статические характеристики: среднее арифмтическое
Статические характеристики: среднее арифмтическое Проверка деления
Проверка деления Карточки по математике
Карточки по математике Приёмы вычитания с переходом через десяток
Приёмы вычитания с переходом через десяток Область визначення функції
Область визначення функції Устная работа. Разложите на множители
Устная работа. Разложите на множители Линейное уравнение с одной переменной. Урок 15
Линейное уравнение с одной переменной. Урок 15 Параллелепипед. Куб
Параллелепипед. Куб Площади и объемы
Площади и объемы Дроби. Зажжение олимпийского огня 7 февраля 2014 года, город Сочи
Дроби. Зажжение олимпийского огня 7 февраля 2014 года, город Сочи Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Письменный прием вычитания
Письменный прием вычитания Геометрические фигуры в жизни и в природе. Проект
Геометрические фигуры в жизни и в природе. Проект Множители и произведение
Множители и произведение Абсолютная величина вектора в пространстве
Абсолютная величина вектора в пространстве Треугольник
Треугольник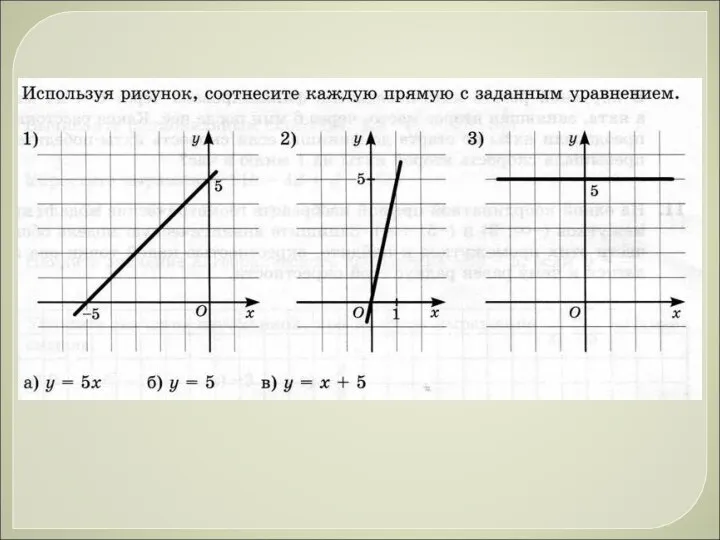 Уравнение, задающее прямую
Уравнение, задающее прямую Устный счет
Устный счет Задачи на построение
Задачи на построение Прикладная статистика. Доверительные интервалы для среднего. Критерий t Стьюдента. Критерии Уилкоксона для ранговых сравнений
Прикладная статистика. Доверительные интервалы для среднего. Критерий t Стьюдента. Критерии Уилкоксона для ранговых сравнений