Содержание
- 2. 1. ВЕКТОРЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
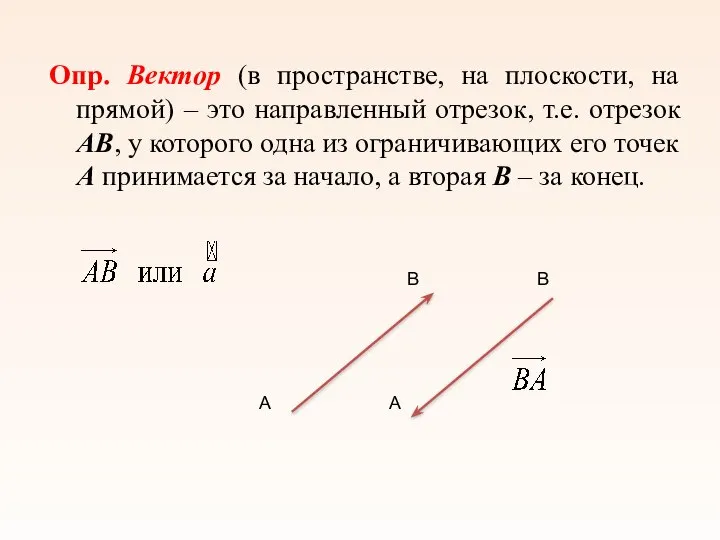
- 3. Опр. Вектор (в пространстве, на плоскости, на прямой) – это направленный отрезок, т.е. отрезок AB, у
- 4. Опр. Ненулевые векторы называются равными: , если: они лежат на одной прямой или на параллельных прямых;
- 5. Операции над векторами
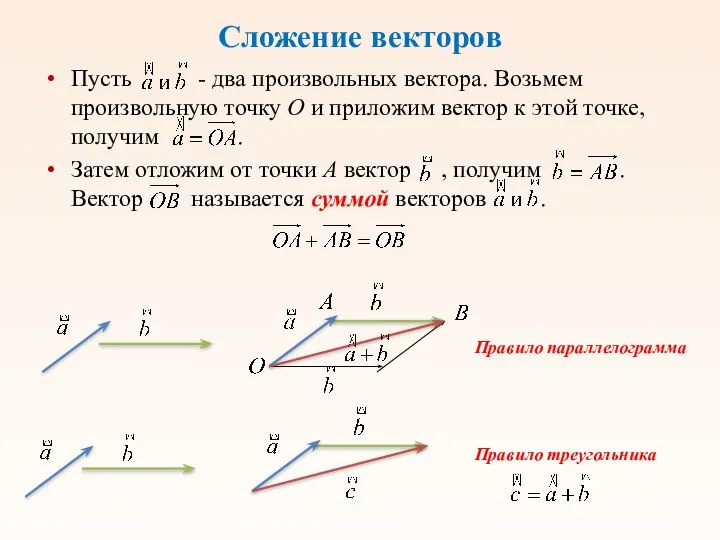
- 6. Сложение векторов Пусть - два произвольных вектора. Возьмем произвольную точку О и приложим вектор к этой
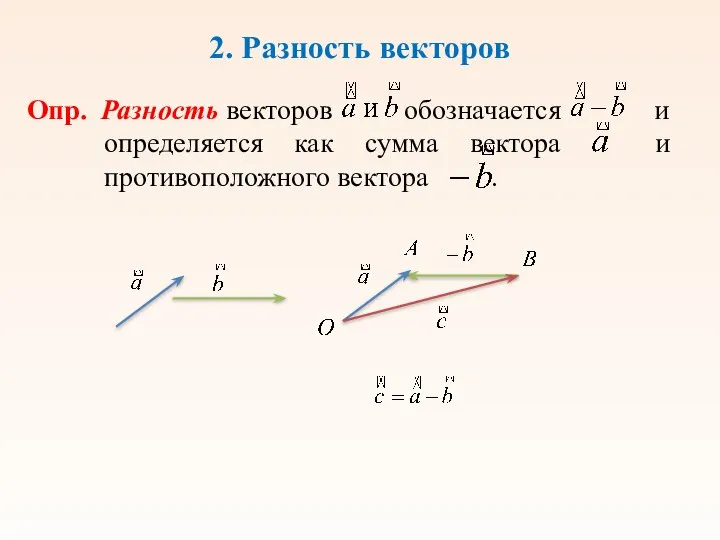
- 7. 2. Разность векторов Опр. Разность векторов обозначается и определяется как сумма вектора и противоположного вектора .
- 8. 3. Умножение вектора на число Опр. Произведение вектора на число λ называется вектор, длина которого равна
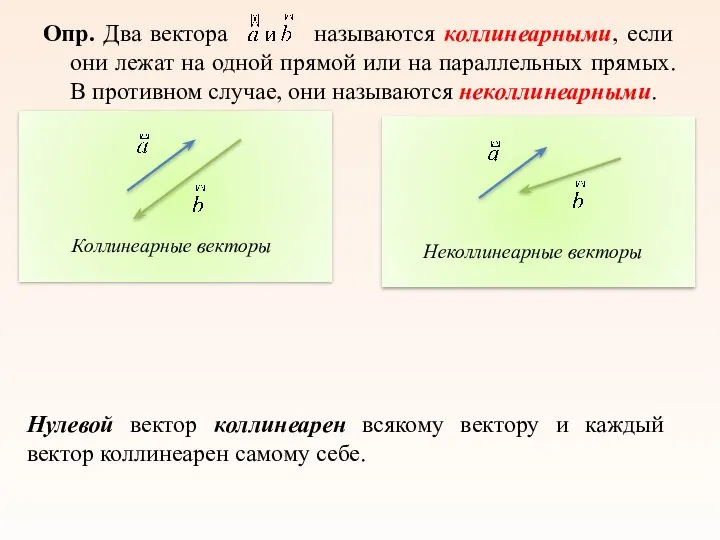
- 9. Опр. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. В
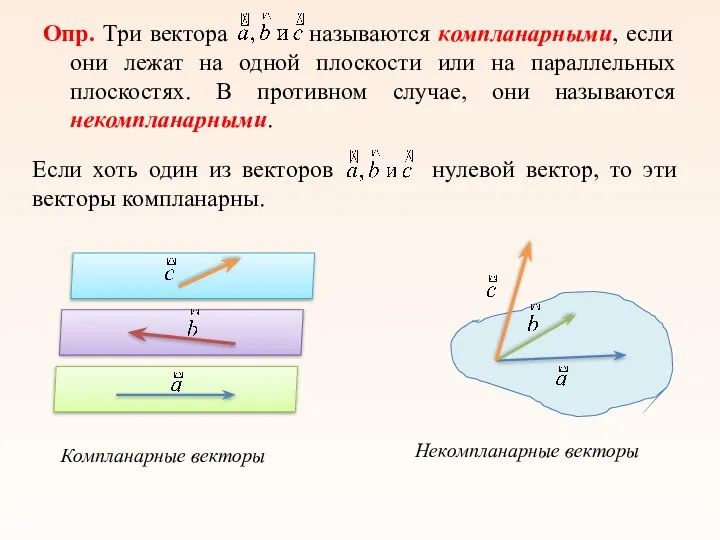
- 10. Опр. Три вектора называются компланарными, если они лежат на одной плоскости или на параллельных плоскостях. В
- 11. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ
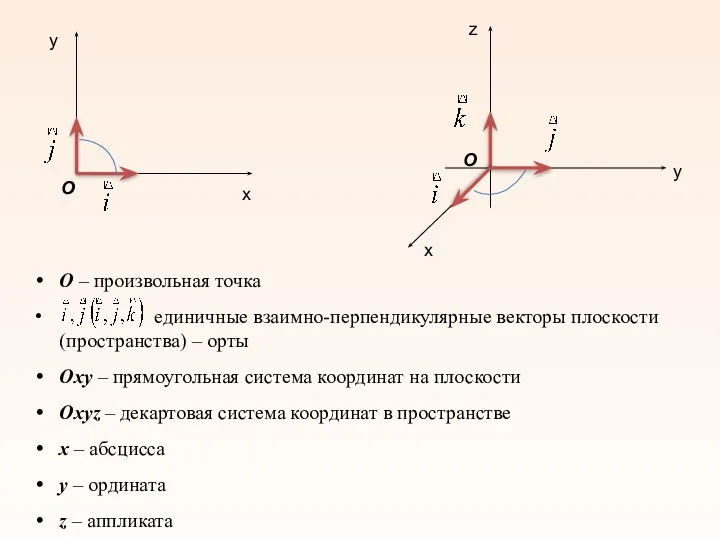
- 12. О – произвольная точка единичные взаимно-перпендикулярные векторы плоскости (пространства) – орты Oxy – прямоугольная система координат
- 13. Вектор заданный на плоскости Oxy, может быть представлен в виде: где x1, y1 – проекции вектора
- 14. Если даны координаты его начальной и конечной точек.
- 15. Условие коллинеарности двух векторов Векторы коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны, т.е.
- 16. Длина вектора в декартовых координатах: Длина вектора в прямоугольных координатах :
- 17. Линейные операции над векторами в координатной форме
- 18. Пример
- 19. СКАЛЯРНОЕ И ВЕКТОРНОЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
- 20. Опр. Скалярным произведением двух векторов называется число, обозначаемое и равное
- 21. . Пример
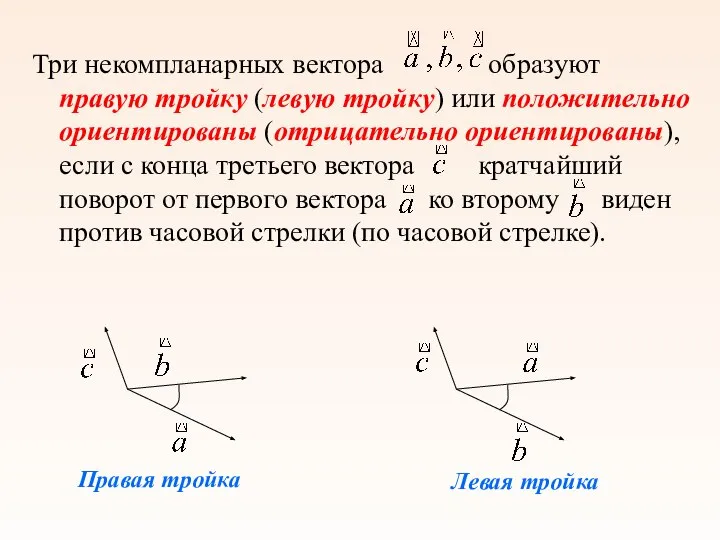
- 22. Три некомпланарных вектора образуют правую тройку (левую тройку) или положительно ориентированы (отрицательно ориентированы), если с конца
- 23. Векторное произведение векторов Опр. Векторным произведением двух векторов называется такой третий вектор , который удовлетворяет следующим
- 24. Обозначения:
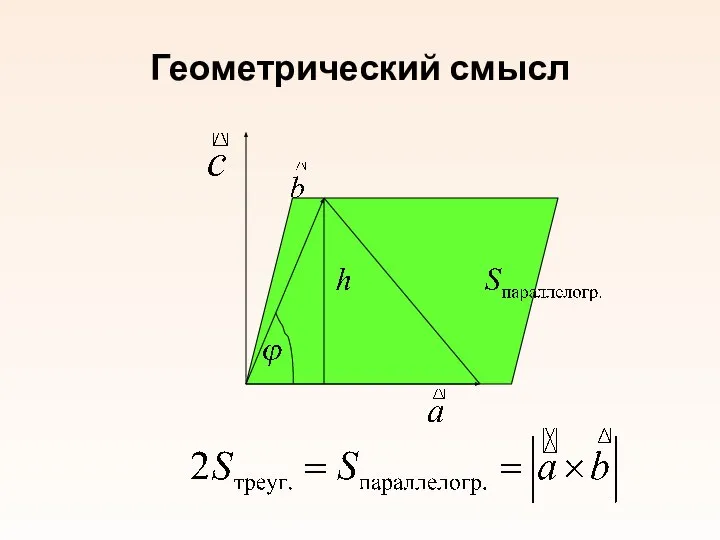
- 25. Геометрический смысл
- 26. 6. Теорема (запись векторного произведения в координатах) Если
- 27. Пример
- 28. Смешанное произведение векторов Опр. Смешанным произведением трех векторов называется число, обозначаемое и определяемое следующим образом
- 29. Геометрический смысл
- 30. 7. Теорема (запись смешанного произведения в координатах) Если
- 32. Скачать презентацию













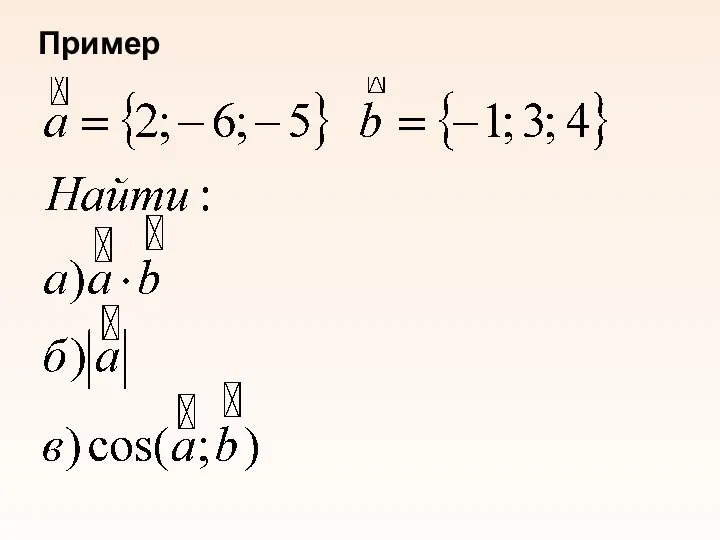







 Перпендикулярные прямые в пространстве
Перпендикулярные прямые в пространстве Сантиметр Цель. В ходе практической работы и наблюдений познакомить учащихся 1 класса с единицей измерения длины – сантиметром.
Сантиметр Цель. В ходе практической работы и наблюдений познакомить учащихся 1 класса с единицей измерения длины – сантиметром. Движение и скорость. Тест
Движение и скорость. Тест Правила теории вероятности
Правила теории вероятности Числа по порялку
Числа по порялку Усеченный конус. Часть 5
Усеченный конус. Часть 5 Системы распознавания образов
Системы распознавания образов Геометрические преобразования
Геометрические преобразования Умножение дробей. Устная работа
Умножение дробей. Устная работа Умножение десятичных дробей
Умножение десятичных дробей Презентация на тему Применение свойств функций к решению уравнений и неравенств
Презентация на тему Применение свойств функций к решению уравнений и неравенств  Понятие вектора
Понятие вектора Урок математики 11.09
Урок математики 11.09 В мире случайных закономерностей. Введение в вероятность. 5 класс
В мире случайных закономерностей. Введение в вероятность. 5 класс Теорема Пифагора (часть 2)
Теорема Пифагора (часть 2) Геометрические преобразования графиков функций
Геометрические преобразования графиков функций Математические ребусы
Математические ребусы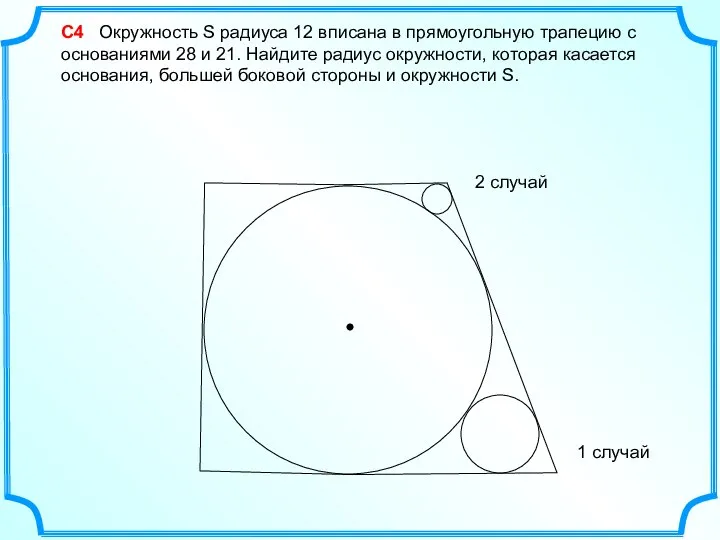 Вписанная окружность. Решение задач
Вписанная окружность. Решение задач Вписанная окружность. Свойство описанного четырехугольника. 8 класс
Вписанная окружность. Свойство описанного четырехугольника. 8 класс Педагогическая диагностика как одно из средств изучения уровня математической подготовки учащихся
Педагогическая диагностика как одно из средств изучения уровня математической подготовки учащихся Анализ результатов диагностики
Анализ результатов диагностики Великолепная пятерка. Игра
Великолепная пятерка. Игра Математический диктант
Математический диктант История системы мер длины (часть 1)
История системы мер длины (часть 1) Четырехугольники: параллелограмм, трапеция, прямоугольник, ромб, квадрат
Четырехугольники: параллелограмм, трапеция, прямоугольник, ромб, квадрат Устный счет на уроках математики в 9 классе по подготовке к экзаменам в форме ОГЭ
Устный счет на уроках математики в 9 классе по подготовке к экзаменам в форме ОГЭ Урок математики 21.09
Урок математики 21.09 Перпендикуляр и наклонная. Угол между прямой и плоскостью
Перпендикуляр и наклонная. Угол между прямой и плоскостью