Содержание
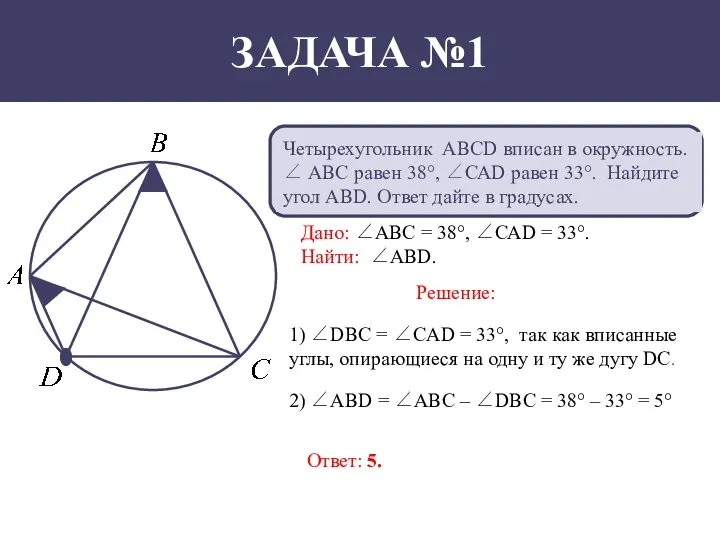
- 2. ЗАДАЧА №1 Четырехугольник АВСD вписан в окружность. ∠ АВС равен 38°, ∠САD равен 33°. Найдите угол
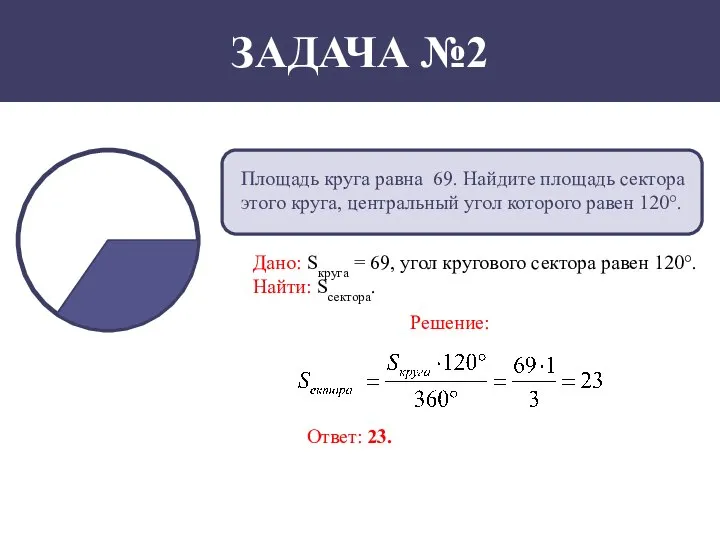
- 3. Площадь круга равна 69. Найдите площадь сектора этого круга, центральный угол которого равен 120°. Дано: Sкруга
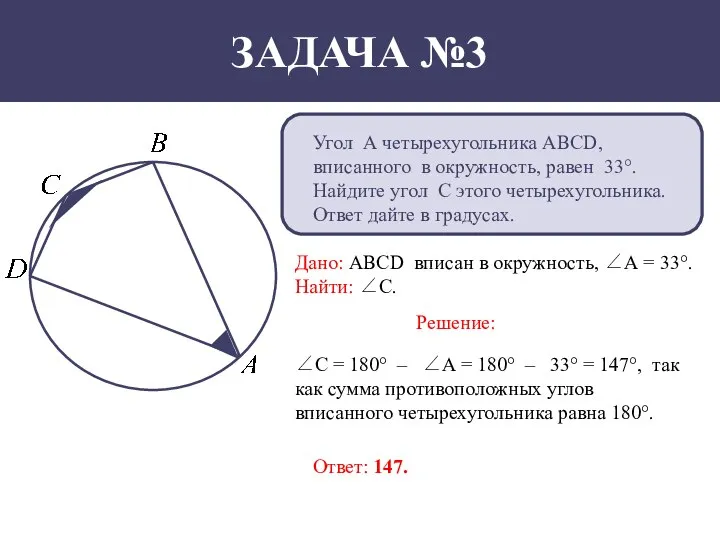
- 4. Угол А четырехугольника АВСD, вписанного в окружность, равен 33°. Найдите угол С этого четырехугольника. Ответ дайте
- 5. Отрезки АС и BD – диаметры окружности с центром О. Угол АСВ равен 53°. Найдите угол
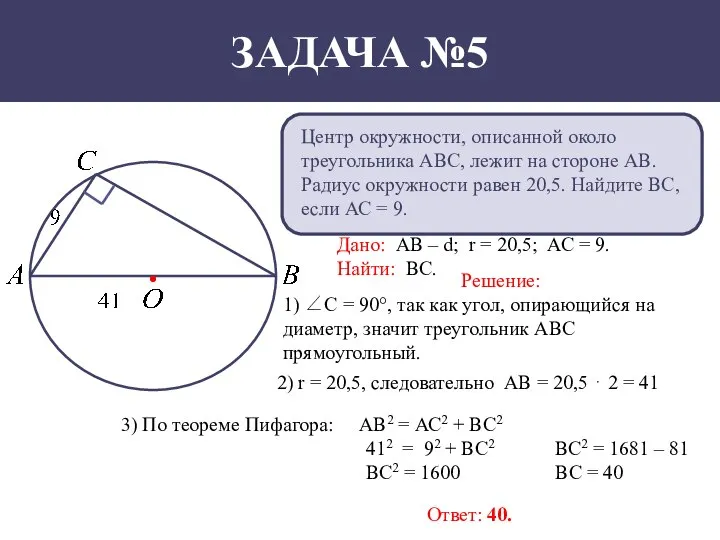
- 6. Центр окружности, описанной около треугольника АВС, лежит на стороне АВ. Радиус окружности равен 20,5. Найдите ВС,
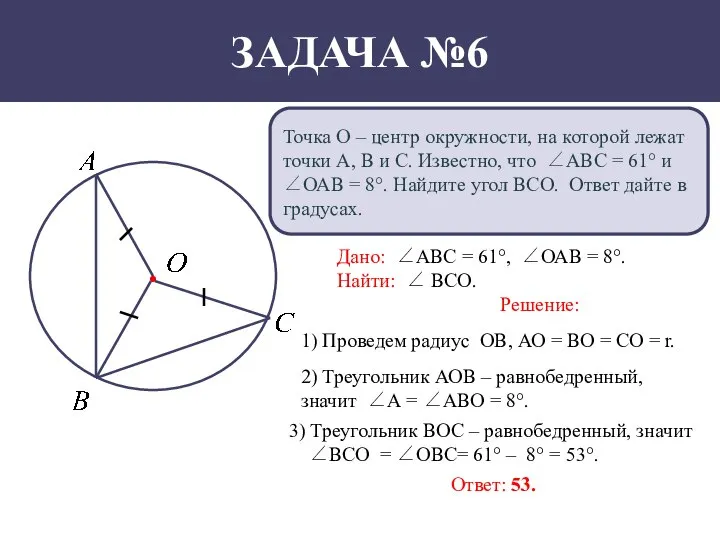
- 7. Точка О – центр окружности, на которой лежат точки А, В и С. Известно, что ∠АВС
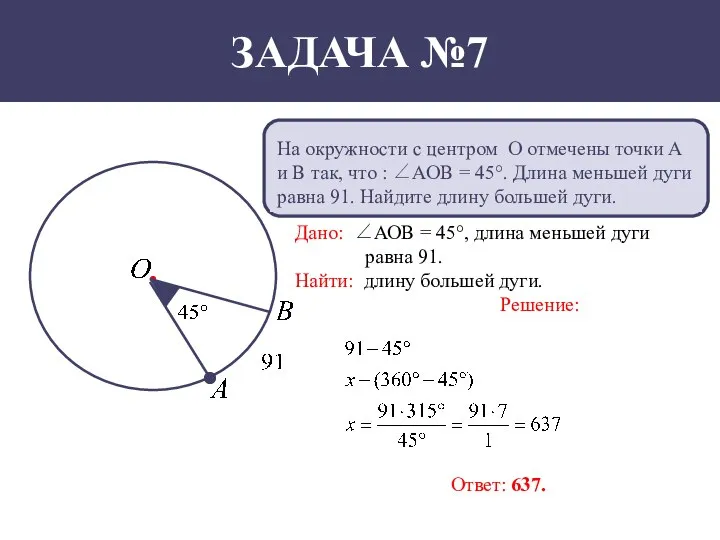
- 8. На окружности с центром О отмечены точки А и В так, что : ∠АОВ = 45°.
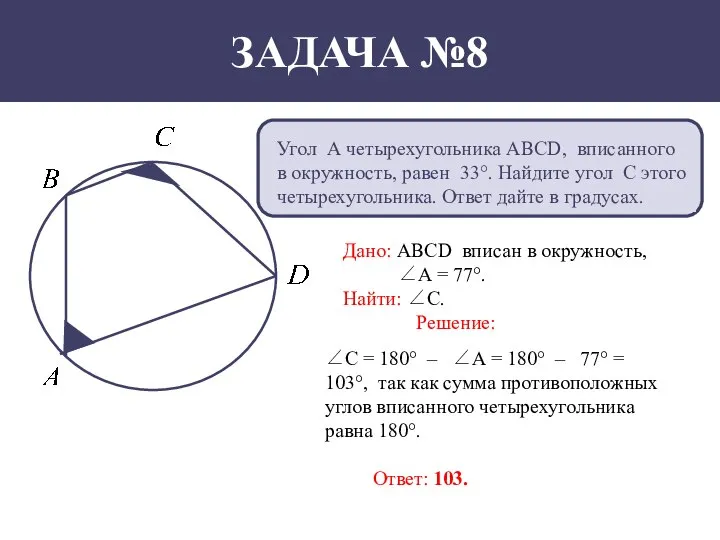
- 9. Угол А четырехугольника АВСD, вписанного в окружность, равен 33°. Найдите угол С этого четырехугольника. Ответ дайте
- 10. Четырехугольник АВСD описан около окружности, АВ = 8, ВС = 12, СD = 13. Найдите АD.
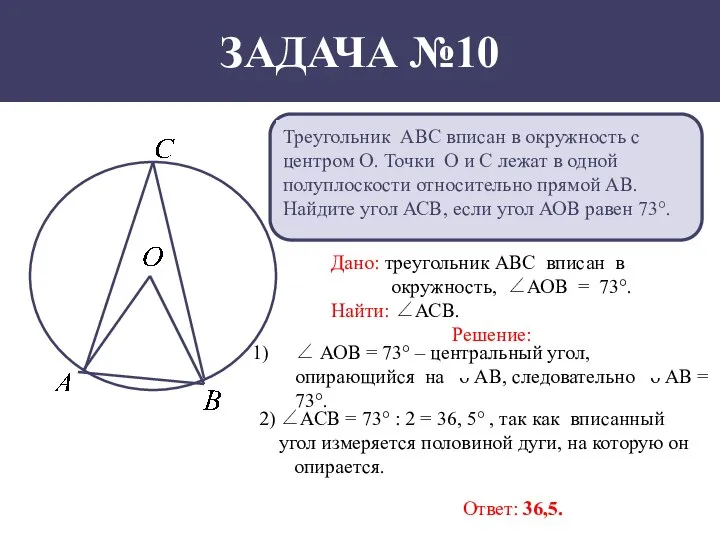
- 11. Треугольник АВС вписан в окружность с центром О. Точки О и С лежат в одной полуплоскости
- 12. ЗАДАЧА №11 Радиус окружности, вписанной в трапецию, равен 12. Найти высоту этой трапеции. Дано: трапеция вписана
- 13. ЗАДАЧА №12 Сторона АВ треугольника АВС проходит через центр описанной около него окружности . Найдите ∠
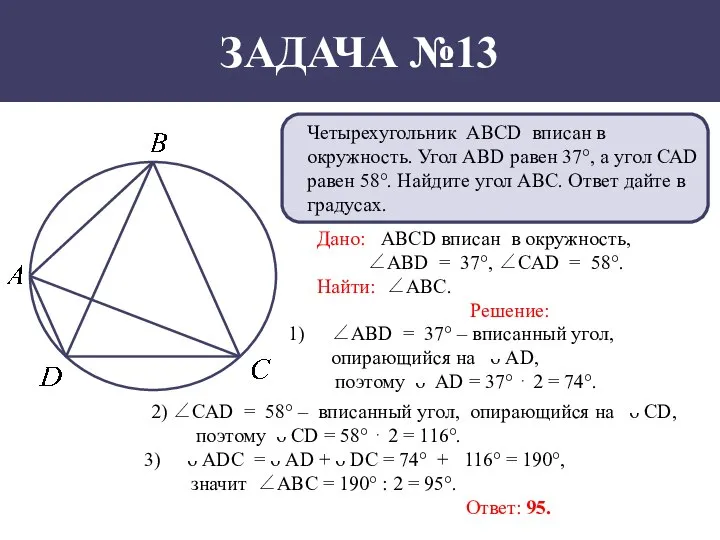
- 14. ЗАДАЧА №13 Четырехугольник АВСD вписан в окружность. Угол АВD равен 37°, а угол САD равен 58°.
- 15. ЗАДАЧА №14 Окружность с центром в точке О описана около равнобедренного треугольника АВС, в котором АВ
- 16. ЗАДАЧА №15 Радиус окружности, вписанной в равносторонний треугольник, равен 6. Найдите высоту этого треугольника. Дано: треугольник
- 17. ЗАДАЧА №16 Через точку А, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в
- 18. ЗАДАЧА №17 Касательные в точках А и В к окружности с центром О пересекаются под углом
- 21. Скачать презентацию









 Формулы сложения
Формулы сложения Углы, связанные с окружностью
Углы, связанные с окружностью Стереометрия. Основные фигуры в пространстве
Стереометрия. Основные фигуры в пространстве Математика. Лекция 2. Ранг матрицы. Системы линейных уравнений
Математика. Лекция 2. Ранг матрицы. Системы линейных уравнений Арифметическая прогрессия. 9 класс
Арифметическая прогрессия. 9 класс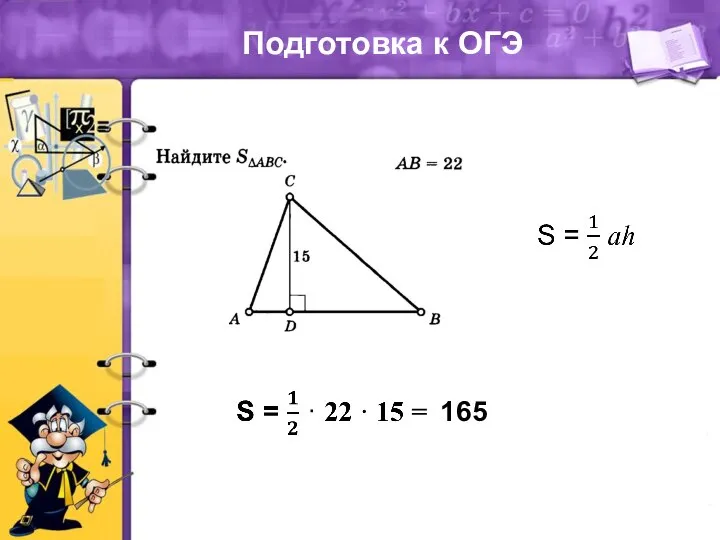 Теорема площади треугольника. Подготовка к ОГЭ
Теорема площади треугольника. Подготовка к ОГЭ Пирамиды. Правильная пирамида
Пирамиды. Правильная пирамида Степень с отрицательным показателем
Степень с отрицательным показателем Математические записи и схемы
Математические записи и схемы Тригонометрия. Комплексные числа
Тригонометрия. Комплексные числа Применение производной к построению графиков функции
Применение производной к построению графиков функции Линейные алгоритмы
Линейные алгоритмы Стереометрия. Базовые понятия. Определения
Стереометрия. Базовые понятия. Определения Презентация на тему Системы линейных уравнений с двумя переменными
Презентация на тему Системы линейных уравнений с двумя переменными  Применение интегральной технологии при изучении алгебраических уравнений
Применение интегральной технологии при изучении алгебраических уравнений Иррациональные неравенства
Иррациональные неравенства Генерация k-элементных подмножеств
Генерация k-элементных подмножеств Урок с применением ИКТ Они были первыми
Урок с применением ИКТ Они были первыми Презентация на тему Площадь многоугольников
Презентация на тему Площадь многоугольников  Математический хоккей
Математический хоккей Математический диктант
Математический диктант Задачи на пропорцию
Задачи на пропорцию Числовые последовательности
Числовые последовательности Угол между векторами
Угол между векторами Малоизвестные, но очень интересные теоремы планиметрии
Малоизвестные, но очень интересные теоремы планиметрии Ознакомление с задачей в 2 действия
Ознакомление с задачей в 2 действия Влияние коэффициентов линейной функции на ее график
Влияние коэффициентов линейной функции на ее график Дроби. Тест
Дроби. Тест