Операции над множествами

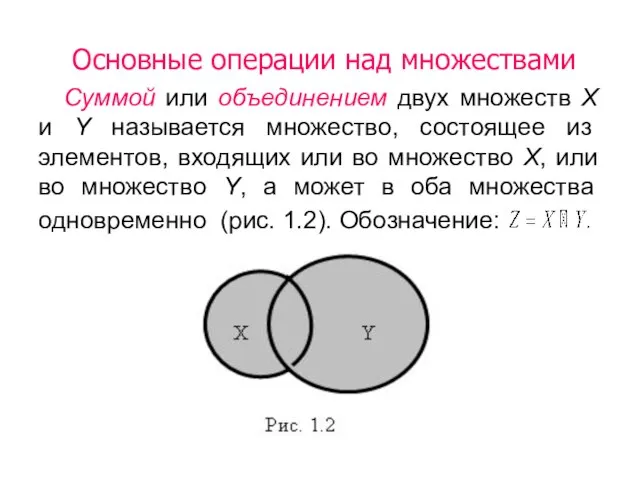
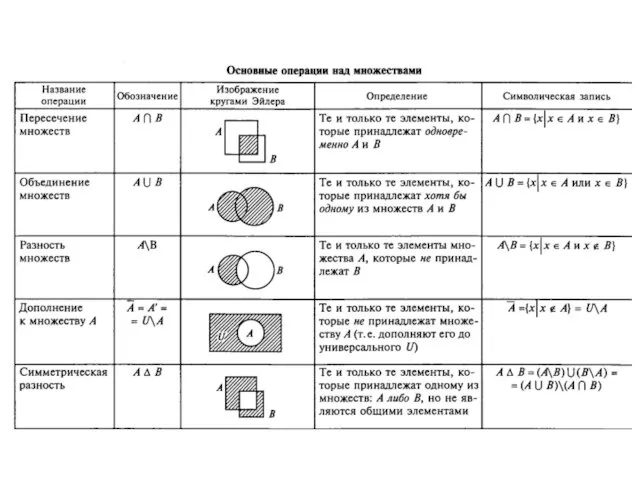
Основные операции над множествами
Суммой или объединением двух множеств Х и Y называется множество, состоящее из элементов, входящих или во множество Х, или во множество Y, а может в оба множества одновременно (рис. 1.2). Обозначение:

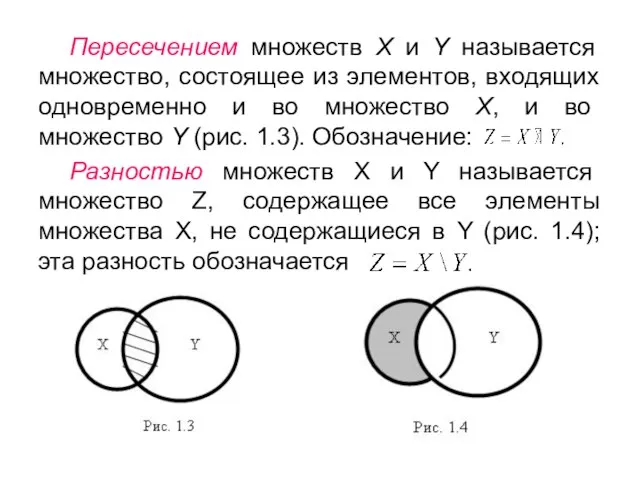
Пересечением множеств Х и Y называется множество, состоящее из элементов, входящих одновременно и во множество Х, и во множество Y (рис. 1.3). Обозначение:
Разностью множеств X и Y называется множество Z, содержащее все элементы множества X, не содержащиеся в Y (рис. 1.4); эта разность обозначается

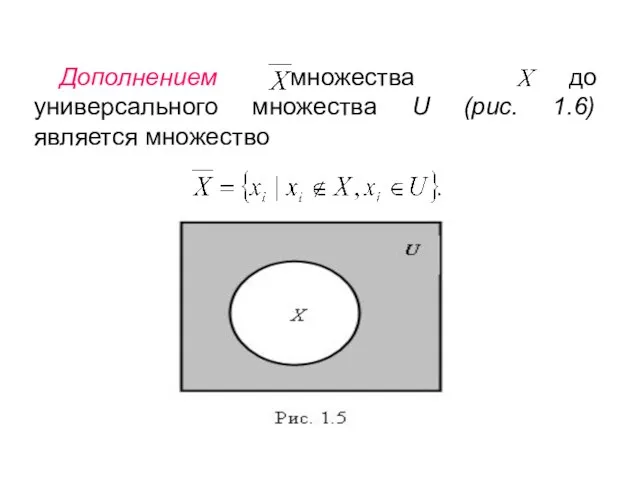
Дополнением множества до универсального множества U (рис. 1.6) является множество

Симметрической разностью множеств X и Y называется множество Z, содержащее либо элементы множества X, либо элементы множества Y, но не те и другие одновременно (рис. 1.6); эта разность обозначается Х Y.
=
Рис. 1.6.

Вместо выражения
«любое х из множества Х»
можно писать , где перевёрнутая латинская буква А взята от начала английского слова Any – любой.
Вместо выражения
«существует элемент х из множества Х»
кратко пишут: , где перевёрнутая латинская буква Е является начальной в английском слове Existence – существование.

Для операций над множествами справедливы следующие тождества:
законы коммутативности объединения и пересечения
законы ассоциативности объединения и пересечения

законы дистрибутивности пересечения относительно объединения и объединения относительно пересечения
законы поглощения
законы склеивания
законы Порецкого
Операция имеет преимущество перед операцией . Скобки - для наглядности.

законы идемпотентности объединения и пересечения
законы действия с универсальным (U) и пустым ( ∅ ) множествами
законы де Моргана
закон двойного дополнения

Универсальное (U) и пустое ( ∅ ) множества являются дополнениями друг друга

В повседневной жизни и математике нам часто приходится иметь дело с упорядоченными множествами — кортежами.
Слово кортеж переводится с французского cortege как торжественная процессия (например, свадебный кортеж).
Кортежи. Декартовы произведения

Треугольник АВС на плоскости задается кортежем из 6 чисел
Где
— координаты вершин.
Слова в предложении, буквы в слове, предложения в тексте — все это примеры кортежей.
Двоичный код является кортежем, состоящим
из цифр 0 и 1.

Кортежем длины n из элементов множества А называется упорядоченная последовательность элементов этого множества.
Кортежи и
называются равными, если они имеют одинаковую длину и их элементы с одинаковыми номерами совпадают, т. е. = , если и для

Например, равны кортежи
так как оба кортежа длины 5 и равны все пары соответствующих элементов данных множеств

В отличие от элементов множества элементы кортежа могут совпадать.
Например, в прямоугольной системе координат координаты точек являются кортежами.
Операция, с помощью которой из двух кортежей длиной k и m можно составить новый кортеж длиной k + m, в котором сначала идут подряд элементы первого кортежа, а затем – элементы второго кортежа, называется соединением кортежей.

Пусть А - конечное множество, элементами которого являются некоторые символы, например цифры, буквы, знаки препинания.
Такие множества принято называть алфавитом над заданным множеством символов. Алфавит есть кортеж попарно различимых символов, называемых буквами алфавита. Элементы множества Ап принято называть словами длины n в алфавите А. Слово над алфавитом есть просто некоторая конечная последовательность символов.
Так, шестизначный телефонный номер является словом длины 6 над алфавитом цифр {0, 1, 2, ..., 9}.

Существуют кортежи, элементы которых являются только нулями или единицами.
Кортеж из нулей и единиц можно рассматривать как двоичное представление натурального числа.
Кортеж, состоящий из единиц и нулей, описывает состояние памяти вычислительных машин, причём память может содержать числа, тексты, команды и т.д.
Кортежи используются в штрих-кодах для сообщения нужной информации о характеристике объекта (белая полоска определённой ширины – 0, чёрная -1).

Декартовым (прямым) произведением множеств называется множество , состоящее из всех кортежей длины k, в которых , где
Поскольку для задания кортежа важен порядок, то порядок множителей важен в декартовом произведении.
Например декартовым произведением множеств и будет являться множество пар
Декартово произведение

Если множества
конечны, то их декартово произведение может быть
представлено в общем виде таблицей из m столбцов и к строк.
Например, декартово произведение X х Y, где
можно представить в виде табл.

Число элементов в декартовом произведении конечных множеств А и В равно произведению числа элементов множества А на число элементов множества В.
Варианты записи: |А х В| = |А| • |В|
или n(А х В) = n(А) • n(В).
Если , то пишут .
называют n-й декартовой степенью множества А.

Примерами декартовых произведений являются таблицы сложения и умножения, все возможные наборы пар координат на плоскости, троек координат некоторой точки в пространстве. Железнодорожный билет тоже является кортежем, а совокупность всех билетов — декартовым произведением множеств паспортов, посадочных станций, станций прибытия, времени и других множеств.

Свое название декартово произведение получило в честь выдающегося французского математика и философа Рене Декарта (1596—1650), являющегося автором знаменитого метода координат.

Вспомните выражение «прямоугольная декартова система координат», причем координаты точек в этой системе также
являются кортежами. На плоскости двумерные кортежи — это пара вида (х;у), а в пространстве — трехмерные кортежи в виде тройки чисел (x; у; z), где элементами кортежа являются
соответствующие координаты точки.