Содержание
- 2. Матрицей размера mxn называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу,
- 3. матрица размерности mxn
- 5. Две матрицы называются равными, если у них одинаковая размерность и совпадают строки и столбцы. Если число
- 6. Пример: - квадратная матрица размерности 3х3
- 7. Матрица, состоящая из одной строки, называется матрицей-строкой или вектором-строкой. матрица-строка
- 8. Матрица, состоящая из одного столбца, называется матрицей-столбцом или вектором-столбцом. матрица-столбец
- 9. Элементы матрицы aij , у которых номер столбца совпадает с номером строки, называются диагональными. Если в
- 10. единичная матрица
- 11. Матрица любого размера называется нулевой, если все ее элементы равны 0. нулевая матрица
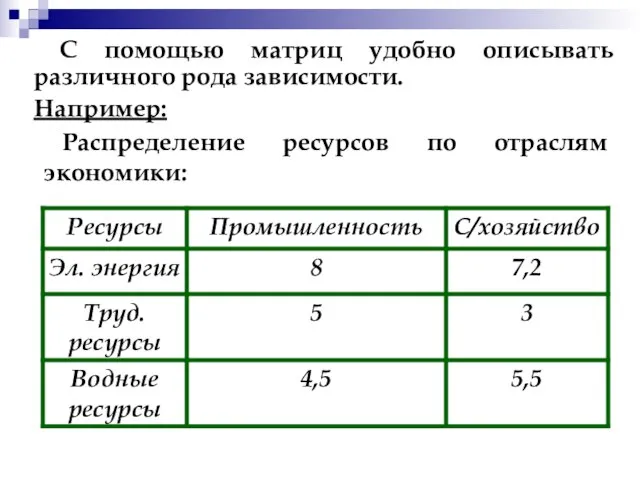
- 12. Распределение ресурсов по отраслям экономики: С помощью матриц удобно описывать различного рода зависимости. Например:
- 13. Эту зависимость можно представить в виде матрицы: Где элемент aij показывает сколько i–го ресурса потребляет j–отрасль.
- 14. ДЕЙСТВИЯ НАД МАТРИЦАМИ 1. Умножение матрицы на число Чтобы умножить матрицу на число, надо каждый элемент
- 15. Пусть дана матрица Умножаем ее на число λ: Где каждый элемент матрицы В: Где:
- 16. Например: Умножая матрицу на число 2, получим:
- 17. 2. Сложение матриц Складываются матрицы одинаковой размерности. Получается матрица той же размерности, каждый элемент которой равен
- 18. Пусть даны матрицы Складываем их: Где каждый элемент матрицы С: Аналогично проводится вычитание матриц.
- 19. Пример Найти сумму и разность матриц:
- 20. Решение:
- 21. Пример Найти сумму матриц:
- 22. 3. Умножение матриц Умножение матриц возможно, если число столбцов первой матрицы равно числу строк второй. Тогда
- 23. Пусть даны матрицы Умножаем их: Где каждый элемент матрицы С:
- 24. Пример Найти произведение матриц:
- 25. Число столбцов первой матрицы равно числу строк второй, следовательно их произведение существует: Решение:
- 26. Теперь перемножим матрицы в обратном порядке: Умножение матриц в общем случае некоммутативно:
- 27. Пример Найти произведение матриц:
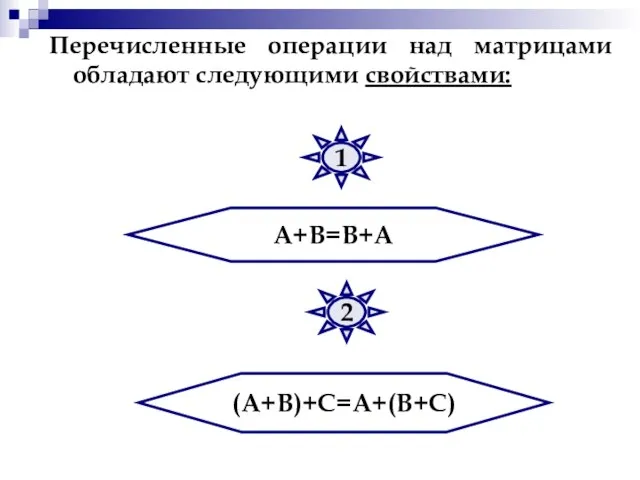
- 28. Перечисленные операции над матрицами обладают следующими свойствами: А+В=В+А (А+В)+С=А+(В+С) 1 2
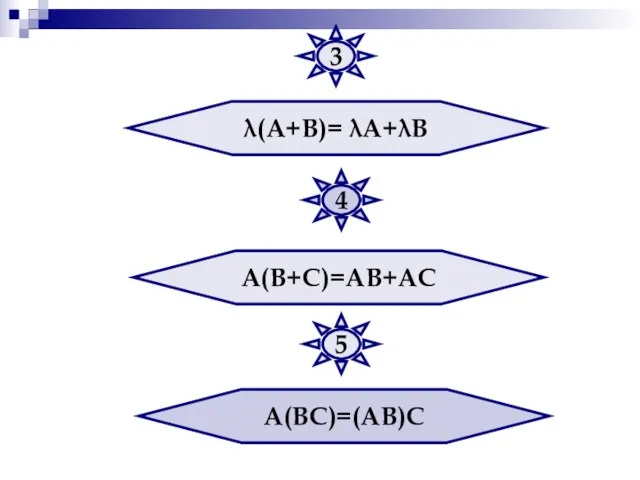
- 29. λ(А+В)= λА+λВ А(В+С)=АВ+АС А(ВС)=(АВ)С 3 4 5
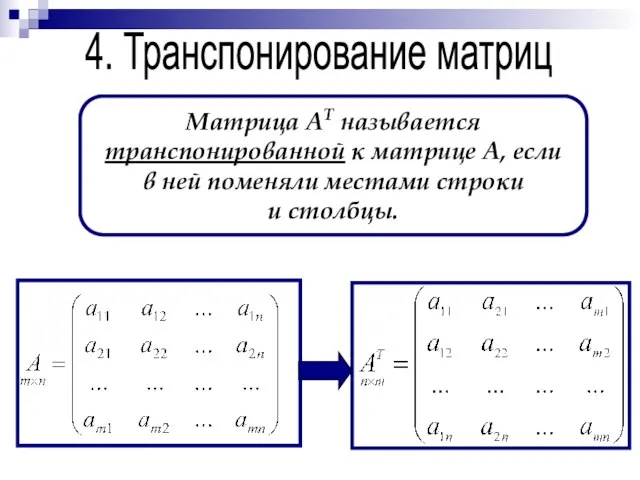
- 30. 4. Транспонирование матриц Матрица АТ называется транспонированной к матрице А, если в ней поменяли местами строки
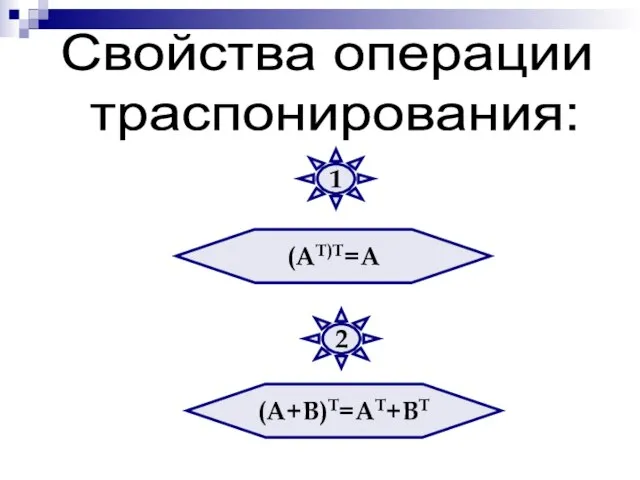
- 31. (АТ)Т=А (А+В)Т=АТ+ВТ Cвойства операции траспонирования: 1 2
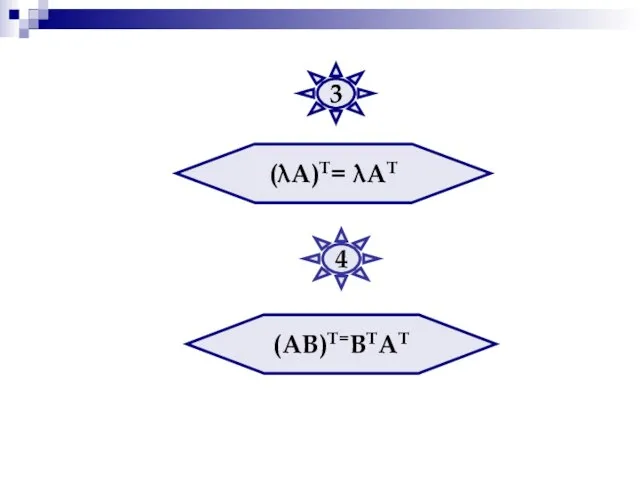
- 32. (λА)Т= λАТ (АВ)Т=ВТАТ 3 4
- 33. Пример Транспонировать матрицу:
- 34. Решение:
- 35. В программировании матрица – это двумерный массив
- 36. Диапазон – это совокупность смежных ячеек, образующих прямоугольную область таблицы, заданную адресами левой верхней и нижней
- 37. B2:B5 - это диапазон из четырех ячеек B2, B3, B4, B5 (вектор- столбец); B2:E2 - это
- 38. Понятие табличных формул Табличные формулы или формулы массива – очень мощное вычислительное средство Excel, позволяющее работать
- 39. Матрицы. Действия с матрицами
- 40. Сложение матриц Аij+Bij = Cij Для сложения и вычитания матриц в Excel не существует специальных функций
- 41. Умножение матриц Для умножения матриц в Excel применяется функция МУМНОЖ(матрица1;матрица2). Ввод функции завершить нажатием клавиши F4
- 43. Скачать презентацию


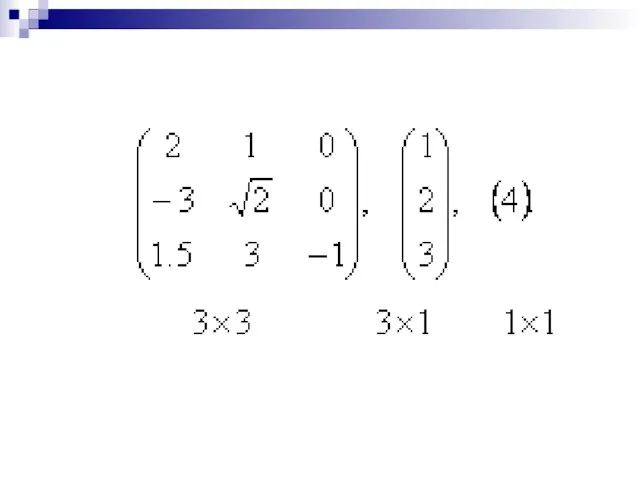































 Урок алгебры в 8 классе
Урок алгебры в 8 классе Задачи ФИПИ
Задачи ФИПИ Тригонометрия в жизни
Тригонометрия в жизни Медиана, биссектриса и высота треугольника
Медиана, биссектриса и высота треугольника Решение примеров и задач с числами, полученными при измерении стоимости
Решение примеров и задач с числами, полученными при измерении стоимости Приборы и инструменты для измерения углов
Приборы и инструменты для измерения углов Тождественные преобразования. 7 класс
Тождественные преобразования. 7 класс Знаки коэффициентов квадратичной функции
Знаки коэффициентов квадратичной функции Решение иррациональных уравнений
Решение иррациональных уравнений Задачи на проценты. Тренировочные задания. 9 класс
Задачи на проценты. Тренировочные задания. 9 класс Скалярное произведение векторов
Скалярное произведение векторов розвязування трикутників
розвязування трикутників Свойства параллелограмма
Свойства параллелограмма Игра- тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление
Игра- тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление Неопределенный интеграл Ч2, свойства неопределенного интеграла
Неопределенный интеграл Ч2, свойства неопределенного интеграла Треугольники и их виды
Треугольники и их виды Письменное умножение на трёхзначное число
Письменное умножение на трёхзначное число Периметр восьмиугольника
Периметр восьмиугольника Векторная алгебра
Векторная алгебра Повторение расширение сведений о функции
Повторение расширение сведений о функции Устный счет. 6 класс
Устный счет. 6 класс Складываемые и вычитаемые числа. Урок 61
Складываемые и вычитаемые числа. Урок 61 Правильные многогранники
Правильные многогранники Решение задача на совместную работу. 6 класс
Решение задача на совместную работу. 6 класс Сложение и вычитание алгебраических дробей
Сложение и вычитание алгебраических дробей Тригонометрия (В5, В7) на ЕГЭ
Тригонометрия (В5, В7) на ЕГЭ Перпендикулярность плоскостей. Параллепипед
Перпендикулярность плоскостей. Параллепипед Площадь многоугольника. Задания для устного счета. Упражнение 5. 8 класс
Площадь многоугольника. Задания для устного счета. Упражнение 5. 8 класс