Основные понятия теории вероятности. Случайные события. Виды случайных событий (лекция 2)

Основы теории вероятностей

Лекция №2
Тема :
Случайные события. Классическое определение вероятности. Алгебра событий Теоремы умножения и сложения вероятностей

Основные вопросы:
Основные понятия теории вероятности. Случайные события. Виды случайных событий.
Классическое определение вероятности случайного события. Основные свойства вероятности случайного события.
Операции над событиями.
Формула умножения теории вероятности. Формула сложения теории вероятности.

Случайность и здравый смысл
«Теория вероятностей есть в сущности не что иное, как здравый смысл, сведенной к исчислению»
Лаплас

СОБЫТИЕ
Под СОБЫТИЕМ понимается явление, которое происходит в результате осуществления какого-либо определенного комплекса условий.
ПРИМЕР. Бросаем шестигранный игральный кубик.
Определим события:
А {выпало четное число очков};
В {выпало число очков, кратное 3};
С {выпало более 4 очков}.
✔

Эксперимент (опыт)
ЭКСПЕРИМЕНТ (или опыт) заключается в наблюдении за объектами или явлениями в строго определенных условиях и измерении значений заранее определенных признаков этих объектов (явлений).
✔

ПРИМЕРЫ
сдача экзамена,
наблюдение за дорожно-транспортными происшествиями,
выстрел из винтовки,
бросание игрального кубика,
химический эксперимент,
и т.п.

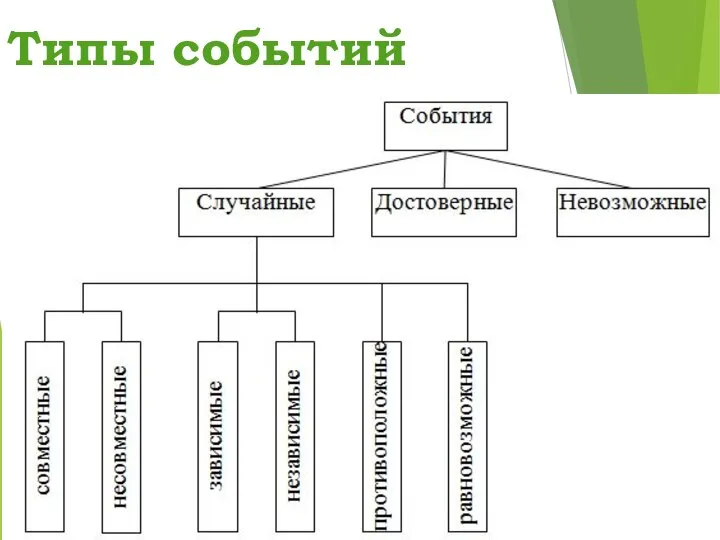
Типы событий

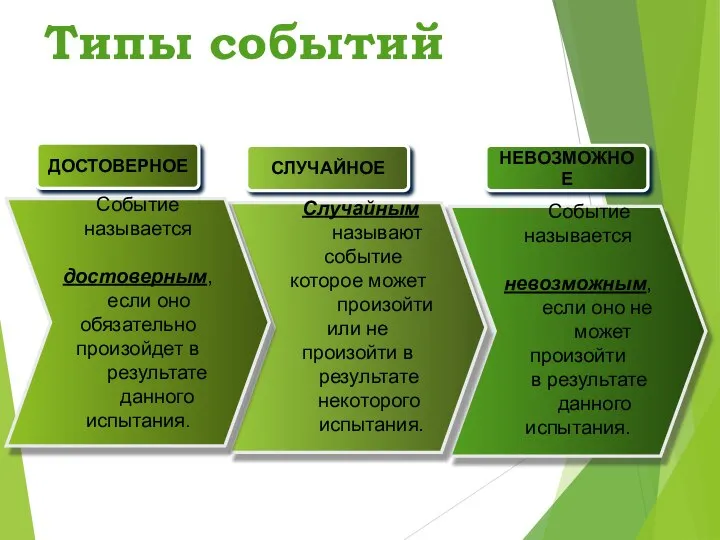
Типы событий
Событие называется
невозможным,
если оно не
может произойти в результате
данного испытания.
Случайным
называют
событие которое может
произойти или не произойти в
результате
некоторого
испытания.
Событие
называется
достоверным,
если оно обязательно произойдет в
результате
данного испытания.
ДОСТОВЕРНОЕ
СЛУЧАЙНОЕ
НЕВОЗМОЖНОЕ

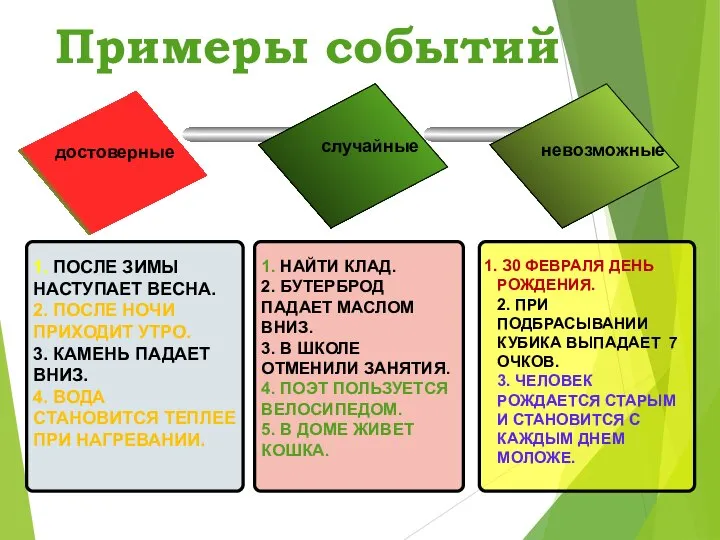
Примеры событий
достоверные
случайные
невозможные
1. ПОСЛЕ ЗИМЫ НАСТУПАЕТ ВЕСНА.
2. ПОСЛЕ НОЧИ ПРИХОДИТ УТРО.
3. КАМЕНЬ ПАДАЕТ ВНИЗ.
4. ВОДА СТАНОВИТСЯ ТЕПЛЕЕ ПРИ НАГРЕВАНИИ.
1. НАЙТИ КЛАД.
2. БУТЕРБРОД ПАДАЕТ МАСЛОМ ВНИЗ.
3. В ШКОЛЕ ОТМЕНИЛИ ЗАНЯТИЯ.
4. ПОЭТ ПОЛЬЗУЕТСЯ ВЕЛОСИПЕДОМ.
5. В ДОМЕ ЖИВЕТ КОШКА.
З0 ФЕВРАЛЯ ДЕНЬ РОЖДЕНИЯ.
2. ПРИ ПОДБРАСЫВАНИИ КУБИКА ВЫПАДАЕТ 7 ОЧКОВ.
3. ЧЕЛОВЕК РОЖДАЕТСЯ СТАРЫМ И СТАНОВИТСЯ С КАЖДЫМ ДНЕМ МОЛОЖЕ.

СЛУЧАЙНОЕ СОБЫТИЕ
СЛУЧАЙНЫМ называют событие, которое может произойти или не произойти в результате некоторого испытания (опыта). Обозначают заглавными буквами А, В, С, Д,… (латинского алфавита).
✔

Определение. Два события, которые в данных условиях могут происходить одновременно, называют совместными.
Определение. События называются несовместными, если появление одного из них исключает появление других (т.е. не могут происходить одновременно).
Определение. События называются равновозможными, если нет оснований считать, что одно из них появится в результате опыта с большей вероятностью.

Два события А и называются противоположными, если не появление одного из них в результате испытания влечет появление другого ( отрицание А).
Если группа событий такова, что в результате испытания обязательно должно произойти хотя бы одно из них и любые два из них несовместны, то эта группа событий называется полной группой событий.

Классическая формула вероятности
Вероятностью события А называется математическая оценка возможности появления этого события в результате опыта.
Вероятность события А равна отношению числа, благоприятствующих событию А исходов опыта к общему числу попарно несовместных исходов опыта, образующих полную группу событий.
N – число всех исходов испытания
М – число исходов благоприятствующих событию А

Свойство вероятности:
Вероятность достоверного события равна 1
Вероятность невозможного события равна 0
Вероятность любого испытания есть неотрицательное число, не превосходящее единицы.
Таким образом, значение вероятности любого события – есть положительное число, заключенное между нулем и единицей.

1) В ящике 4 черных и 6 белых шаров, извлекают 1 шар , какова вероятность что шар будет белым, черным ?
N=10; М=6; А- Извлечение белого шара
N=10; М=4; А- Извлечение черного шара
2) В ящике 10 шаров 2 черных, 4 белых, 4 красных, извлекают 1 шар. Какова вероятность, что он:
А- черный; В- белый; С- красный; D- зеленый
N=10; М=2
N=10; М=4
N=10; М=0
N=10; М=4

Определение.
Относительной частотой события А называется отношение числа опытов, в результате которых произошло событие А к общему числу опытов.
Отличие относительной частоты от вероятности заключается в том, что вероятность вычисляется без непосредственного произведения опытов, а относительная частота – после опыта.
Относительную частоту появления события называют статистической вероятностью.

Операции над событиями
События А и В называются равными, если осуществление события А влечет за собой осуществление события В и наоборот.
Объединением или суммой событий двух событий А и В называется событие С, которое означает появление хотя бы одного из событий А или В (безразлично, какого именно, или обоих, если это возможно).

Операции над событиями
Символически объединение(сумма)записывают так :
С = А + В или

Операции над событиями
Пересечением или произведением событий двух событий А и В называется событие С, которое заключается в осуществлении всех событий и А, и В.
Символически произведение записывают так:
С = АВ или

Операции над событиями
Разностью событий А и В называется событие С, которое означает, что происходит событие А, но не происходит событие В.

Общая схема решения задач
Определить, в чем состоит случайный эксперимент и какие у него элементарные события (исходы). Убедиться, что они равновозможны.
Найти общее число элементарных событий N.
Определить, какие элементарные события благоприятствуют интересующему нас событию А, и найти их число N(А).
4. Найти вероятность события А по формуле P(A)=

Вася, Петя, Коля, Леша бросили жребий – кому начинать игру. Найдите вероятность того, что начинать игру должен будет Петя.
Решение.
1. Случайный эксперимент – бросание жребия.
2. Элементарное событие в этом эксперименте - участник, который выиграл жребий. Перечислим их: (Вася), (Петя), (Коля), (Леша).
Общее число элементарных событий N=4.
Жребий подразумевает, что элементарные события равновозможны.
3. Событию А={жребий выиграл Петя} благоприятствует только одно элементарное событие (Петя). Поэтому N(A)=1.
4. Тогда Р(А)=1/4=0,25
Ответ: 0,25.

Игральный кубик (кость) бросили один раз. Какова вероятность того, что выпало число очков, большее чем 4?
Решение.
Случайный эксперимент – бросание кубика.
2. Элементарное событие – число на выпавшей грани.
Граней всего 6, то есть N=6.
Событию А ={выпало больше чем 4} благоприятствуют два элементарных события: 5 и 6.
Поэтому N(A)=2.
Все элементарные события равновозможны,
поэтому Р(А)=2/6=1/3.
Ответ: 1/3.

В случайном эксперименте монету бросили три раза. Какова вероятность того, что орел выпал ровно два раза?
Решение.
Орел обозначим буквой О, решку –
буквой Р.
Элементарные исходы – тройки,
составленные из букв О и Р.
Выпишем их все:
ООО, ООР, ОРО, ОРР, РОО, РОР, РРО, РРР
3. Всего исходов 8. Значит N=8.
4. Событию А={орел выпал ровно два раза}, благоприятствуют элементарные события ООР, ОРО, РОО, поэтому N(A)=3.
5. Тогда Р(А)=3/8=0,375
Ответ. 0,375

В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
Решение.
Орел обозначим буквой О, решку – буквой Р.
2. Выпишем элементарные исходы: ОО, ОР, РО, РР.
Значит N=4.
3. Событию А={выпал ровно один орел}
Благоприятствуют элементарные события ОР и РО.
Поэтому N(A)=2.
4. Тогда Р(А)=2/4=0,5.
Ответ. 0,5

В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7 спортсменов из Дании, 9 спортсменов из Швеции, 5 – из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.
Решение.
Элементарный исход – спортсмен, который выступает последним. Последним может оказаться любой. Всего спортсменов 25, то есть N=25.
Событию А={последний из Швеции} благоприятствуют только девять исходов, поэтому N(A)=9, тогда Р(А)=9/25=0,36.
Ответ. 0,36.

На экзамене по геометрии школьнику достается один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему: «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение.
Определим события:
А={вопрос на тему «Вписанная окружность}
В={вопрос на тему «Параллелограмм»}
2. События А и В несовместны, так как по условию в списке нет вопросов, относящихся к этим двум темам одновременно.

На экзамене по геометрии школьнику достается один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему: «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
3. Событие С={вопрос по одной из этих двух тем} является их объединением:
4. Применим формулу сложения вероятностей несовместных событий:
Р(С)=Р(А)+Р(В)=0,2+0,15=0,35
Ответ. 0,35

Теорема 1 (сложения вероятностей несовместных событий)
✔
Если случайные события А и В являются несовместными событиями с известными вероятностями, то справедлива следующая теорема.
Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.

Следствие 1: Если события образуют полную группу несовместных событий, то сумма их вероятностей равна единице.
Следствие 2: Сумма вероятностей противоположных событий равна единице.

✔
Теорема 2 (сложения вероятностей совместных событий)
Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.

Определение. Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет.
Определение. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Теорема произведения вероятностей независмых событий
Вероятность произведения двух независимых событий равна произведению вероятностей событий
✔