Содержание
- 2. ЛОГИКА — это наука о формах и законах человеческого мышления и, в частности, о законах доказательных
- 3. ВЫСКАЗЫВАНИЕ - это повествовательное предложение, о котором можно сказать, что оно или истинно или ложно. Например:
- 4. Не всякое предложение является высказыванием: 1) Восклицательные и вопросительные предложения высказываниями не являются. - “Какого цвета
- 5. Высказывания могут быть простыми и сложными. Высказывание считается простым, если никакую его часть нельзя рассматривать как
- 6. Высказывание, которое можно разложить на части, называется сложным Сложное высказывание получается путем объединения простых высказываний логическими
- 7. В математической логике не рассматривается конкретное содержание высказывания, важно только, истинно оно или ложно. Поэтому высказывание
- 8. Таблицы истинности Для каждого составного высказывания (логического выражения) можно построить таблицу истинности, которая определяет истинность или
- 9. Основные логические операции
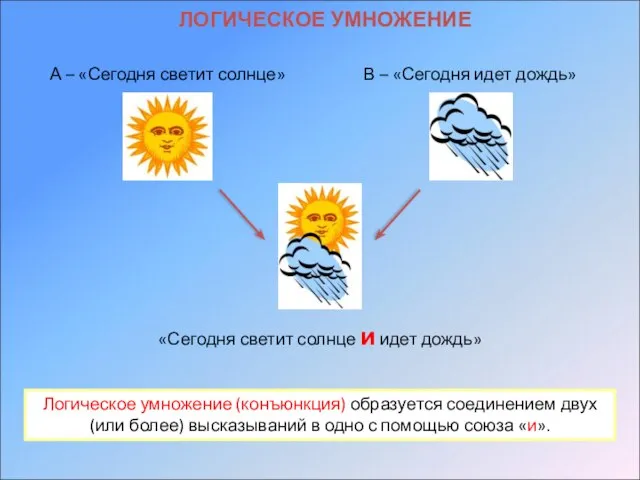
- 10. ЛОГИЧЕСКОЕ УМНОЖЕНИЕ «Сегодня светит солнце и идет дождь» А – «Сегодня светит солнце» В – «Сегодня
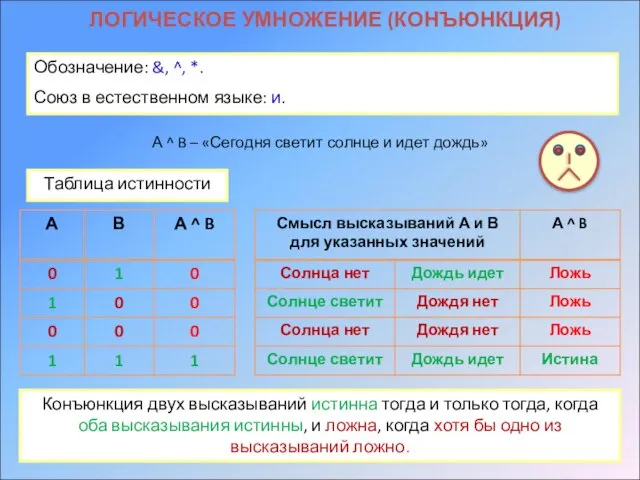
- 11. ЛОГИЧЕСКОЕ УМНОЖЕНИЕ (КОНЪЮНКЦИЯ) Обозначение: &, ^, *. Союз в естественном языке: и. А ^ B –
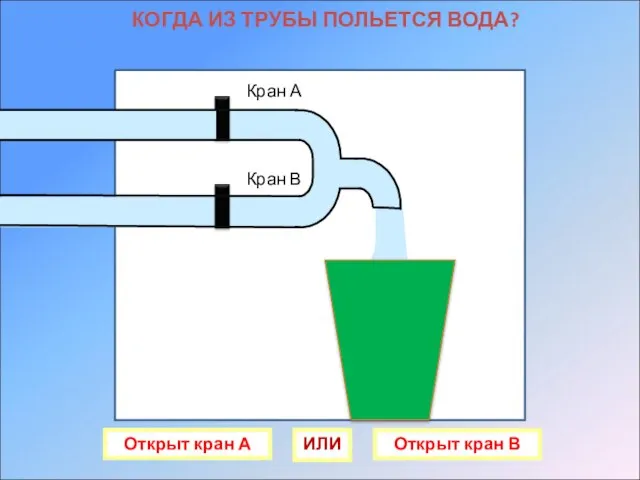
- 12. Кран А Кран В КОГДА ИЗ ТРУБЫ ПОЛЬЕТСЯ ВОДА? Открыт кран А Открыт кран В ИЛИ
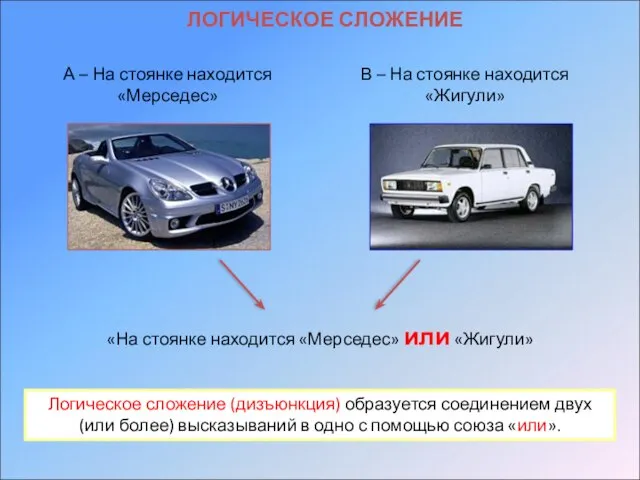
- 13. ЛОГИЧЕСКОЕ СЛОЖЕНИЕ «На стоянке находится «Мерседес» или «Жигули» А – На стоянке находится «Мерседес» В –
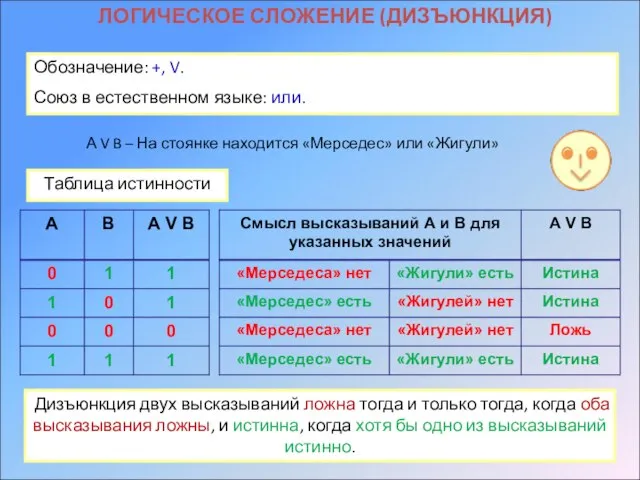
- 14. ЛОГИЧЕСКОЕ СЛОЖЕНИЕ (ДИЗЪЮНКЦИЯ) Обозначение: +, V. Союз в естественном языке: или. А V B – На
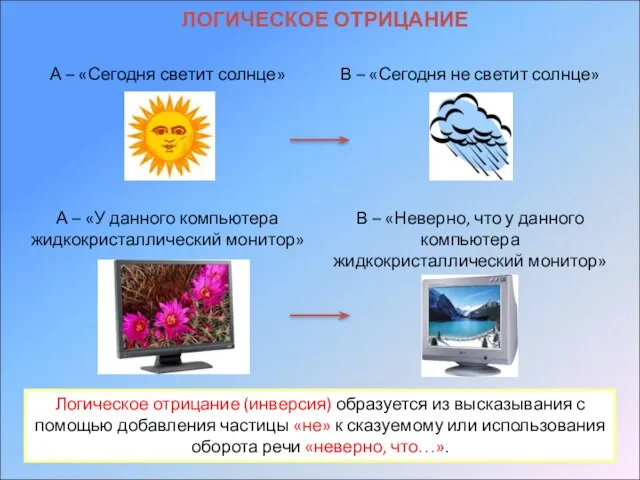
- 15. ЛОГИЧЕСКОЕ ОТРИЦАНИЕ А – «Сегодня светит солнце» В – «Сегодня не светит солнце» Логическое отрицание (инверсия)
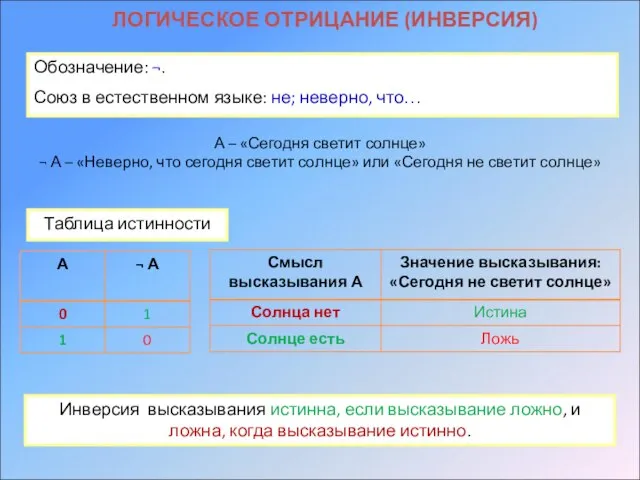
- 16. ЛОГИЧЕСКОЕ ОТРИЦАНИЕ (ИНВЕРСИЯ) Обозначение: ¬. Союз в естественном языке: не; неверно, что… А – «Сегодня светит
- 18. Скачать презентацию








 Операции алгебры логики
Операции алгебры логики Решение задач с помощью уравнений. Урок математики в 5 классе
Решение задач с помощью уравнений. Урок математики в 5 классе Теория игр
Теория игр Равенство треугольников
Равенство треугольников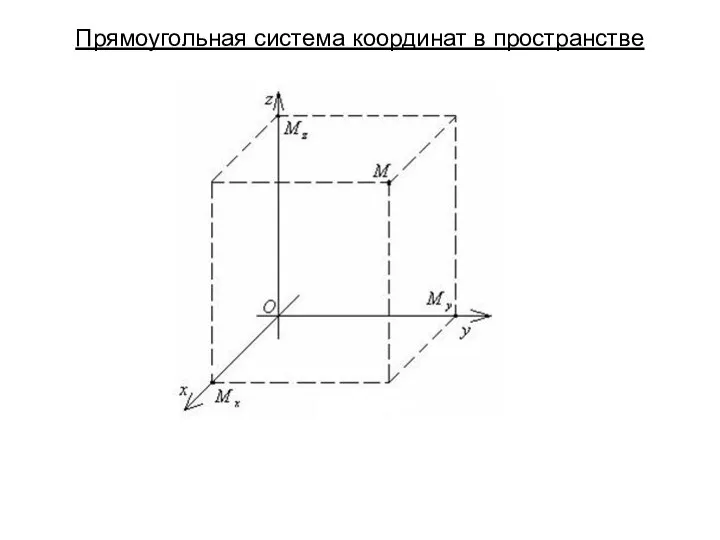 Прямоугольная система координат в пространстве. Понятие вектора
Прямоугольная система координат в пространстве. Понятие вектора Презентация на тему Квадрат суммы и квадрат разности (7 класс)
Презентация на тему Квадрат суммы и квадрат разности (7 класс)  Признаки существования предела
Признаки существования предела Площади фигур. 8 класс
Площади фигур. 8 класс Обобщение пропорции и лекарственные растения Сибири
Обобщение пропорции и лекарственные растения Сибири Презентация по математике "Письменные приёмы умножения" -
Презентация по математике "Письменные приёмы умножения" -  Анализ задач и альтернативные методы решений. Мастер-класс
Анализ задач и альтернативные методы решений. Мастер-класс Сложение чисел с разными знаками
Сложение чисел с разными знаками Обобщающий урок по начертательной геометрии прямая. Плоскость
Обобщающий урок по начертательной геометрии прямая. Плоскость Декартова система координат в пространстве
Декартова система координат в пространстве Луч. Дополнительные лучи. 5 класс
Луч. Дополнительные лучи. 5 класс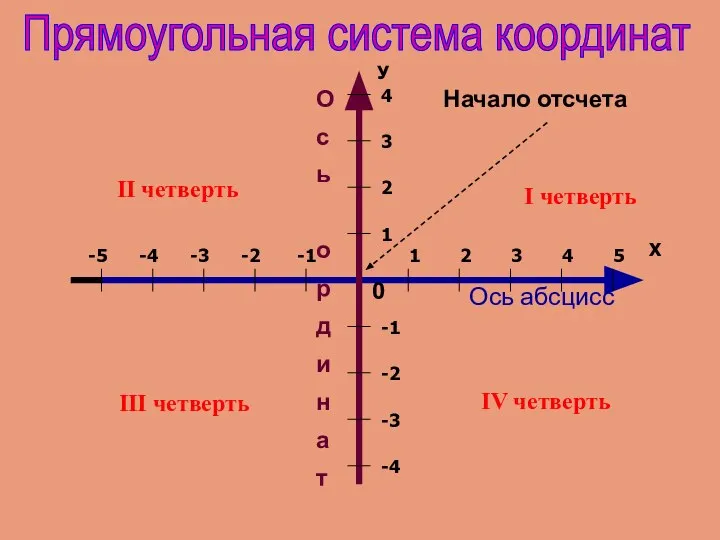 Ось абсцисс
Ось абсцисс Составление арифметических задач
Составление арифметических задач Алгоритм решения задач на нахождение слагаемых по сумме и разности
Алгоритм решения задач на нахождение слагаемых по сумме и разности Матрицы
Матрицы Декартова система координат на плоскости. Математика, 6 класс
Декартова система координат на плоскости. Математика, 6 класс Площадь круга и площадь кругового сегмента
Площадь круга и площадь кругового сегмента Решение задач по теме Объемы тел
Решение задач по теме Объемы тел Презентация на тему Геометрические построения в школьном курсе математики
Презентация на тему Геометрические построения в школьном курсе математики  Окружность
Окружность Через точку А провести профильную прямую ВС, равнонаклоненную к плоскости П1 и плоскости П2. (задача 20)
Через точку А провести профильную прямую ВС, равнонаклоненную к плоскости П1 и плоскости П2. (задача 20) Решение уравнений методом замены переменной
Решение уравнений методом замены переменной Презентация на тему Теоремы синусов и косинусов
Презентация на тему Теоремы синусов и косинусов  Свойства квадратных корней
Свойства квадратных корней