Отыскание точек экстремума

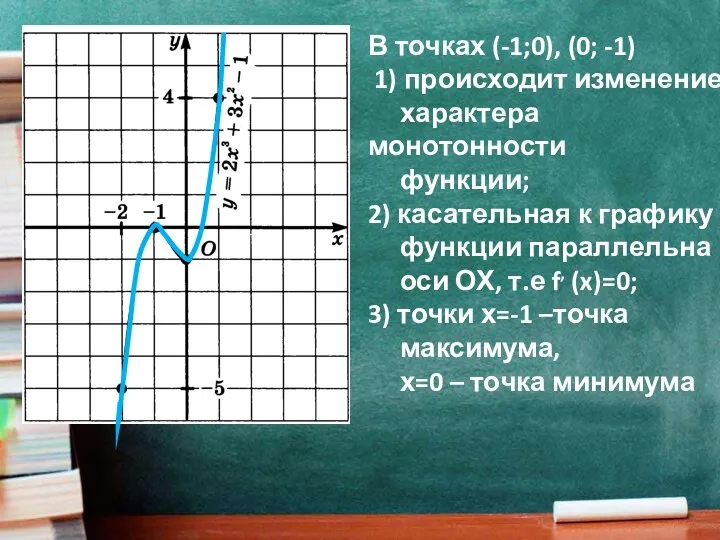
В точках (-1;0), (0; -1)
1) происходит изменение
характера монотонности функции;
2) касательная к графику
функции параллельна
оси ОХ, т.е f, (x)=0;
3) точки х=-1 –точка
максимума,
х=0 – точка минимума

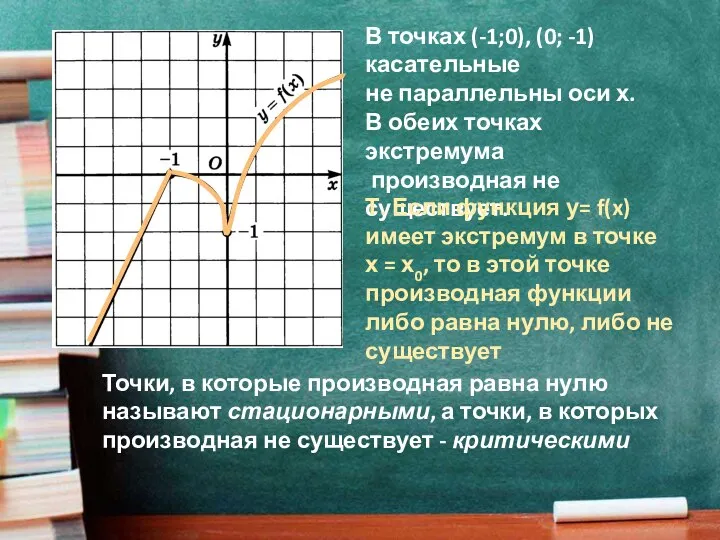
В точках (-1;0), (0; -1)
касательные
не параллельны оси х.
В обеих точках экстремума
производная не существует.
Т. Если функция у= f(x) имеет экстремум в точке х = х0, то в этой точке производная функции либо равна нулю, либо не существует
Точки, в которые производная равна нулю называют стационарными, а точки, в которых производная не существует - критическими

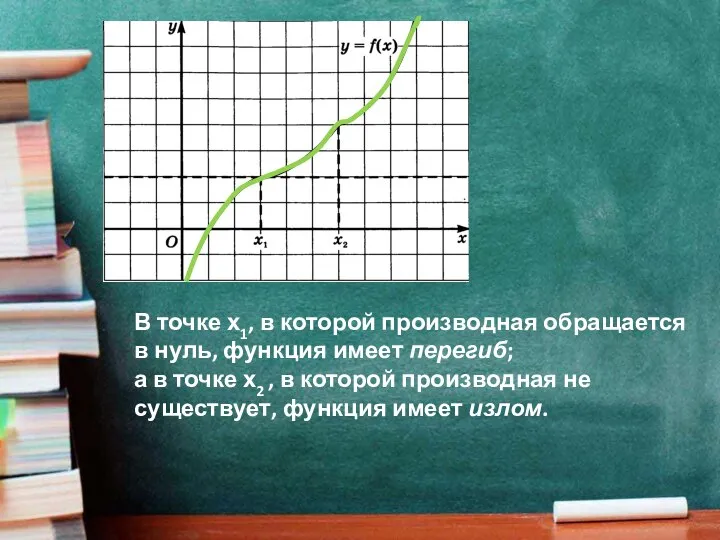
В точке х1, в которой производная обращается в нуль, функция имеет перегиб;
а в точке х2 , в которой производная не существует, функция имеет излом.

Найдите промежутки монотонности:

Достаточные условия существования экстремумов

Найдите экстремумы функции: