Методы решения задач на тему Сфера. Шар

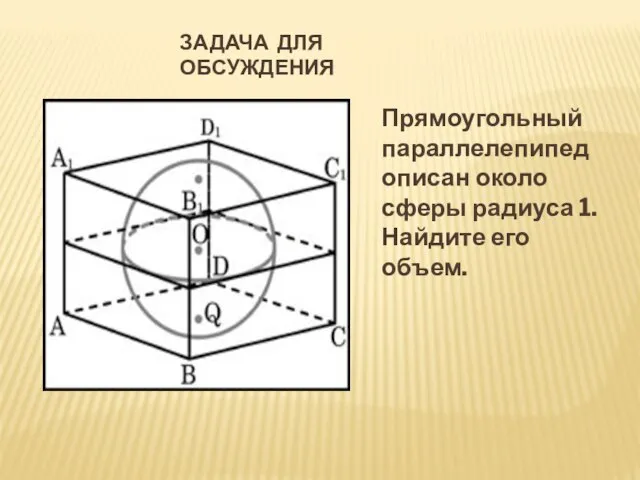
ЗАДАЧА ДЛЯ ОБСУЖДЕНИЯ
Прямоугольный параллелепипед описан около сферы радиуса 1. Найдите его объем.

Продолжить предложения:
1. Шар – это …
2. Сфера – это…
3. Шар отличается от сферы тем, что …
4. Основные формулы для шара: …
5. Основные формулы для сферы: …
6. Шаровой сегмент – это…
7. Расчётные формулы для шарового сегмента: …
8. Шаровой слой – это …
9. Расчётные формулы для шарового слоя: …
10. Шаровой сектор – это …
11. Расчётные формулы для шарового сектора: …

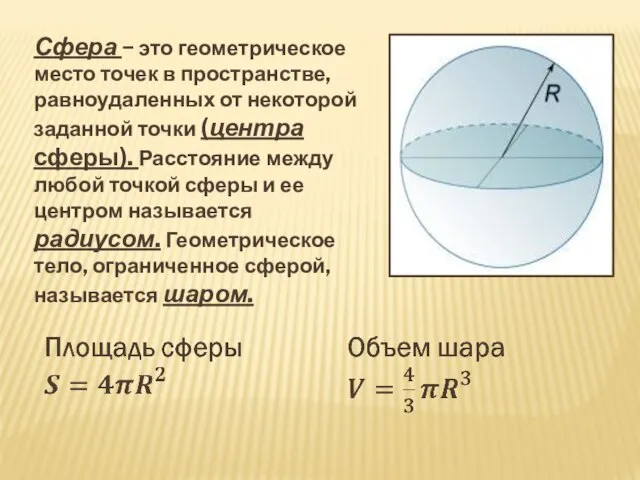
Сфера − это геометрическое место точек в пространстве, равноудаленных от некоторой заданной точки (центра сферы). Расстояние между любой точкой сферы и ее центром называется радиусом. Геометрическое тело, ограниченное сферой, называется шаром.

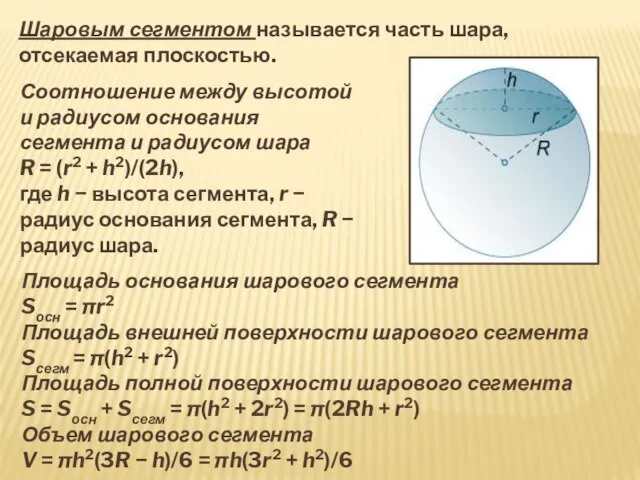
Шаровым сегментом называется часть шара, отсекаемая плоскостью.
Соотношение между высотой и радиусом основания сегмента и радиусом шара
R = (r2 + h2)/(2h),
где h − высота сегмента, r − радиус основания сегмента, R − радиус шара.
Площадь основания шарового сегмента
Sосн = πr2
Площадь внешней поверхности шарового сегмента
Sсегм = π(h2 + r2)
Площадь полной поверхности шарового сегмента
S = Sосн + Sсегм = π(h2 + 2r2) = π(2Rh + r2)
Объем шарового сегмента
V = πh2(3R − h)/6 = πh(3r2 + h2)/6

Шаровым слоем называется часть шара, заключенная между двумя параллельными плоскостями.
Площадь внешней поверхности шарового слоя
Sсл = 2πRh,
где h − высота шарового слоя, R − радиус шара.
Площадь полной поверхности шарового слоя
S = Sсл + S1 + S2 = π(2Rh + r12 + r22),
где h − высота шарового слоя, R − радиус шара, r1, r2 − радиусы оснований шарового слоя, S1, S2 − площади этих оснований.
Объем шарового слоя
V = πh(3r12 + 3r22 + h2)/6,
где r1, r2 − радиусы оснований шарового слоя, h − его высота.

Шаровым сектором называется часть шара, состоящая из шарового сегмента и конуса с вершиной в центре шара и основанием, совпадающим с основанием шарового сегмента. Здесь подразумевается, что шаровой сегмент меньше полушара.
Площадь полной поверхности шарового сектора
S = πR(2h + r),
где h − высота соответствующего шарового сегмента,
r − радиус основания шарового сегмента (или конуса),
R − радиус шара.
Объем шарового сектора
V = 2πR2h/3

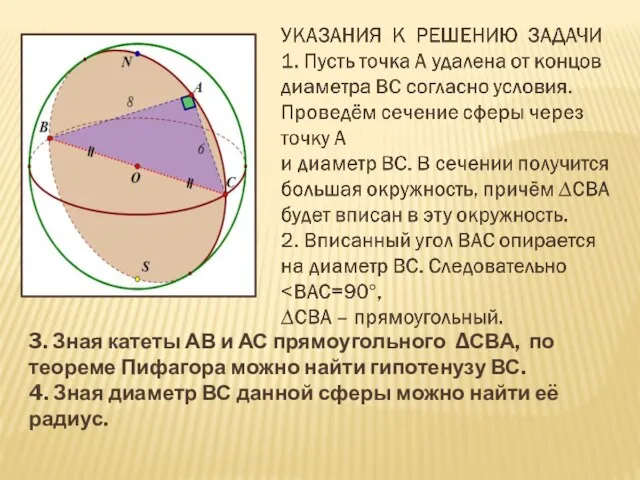
Точка А сферы удалена от концов её диаметра на расстояния равные 6 см и 8 см. Вычислите площадь поверхности сферы.
Предложите способы решения задачи:

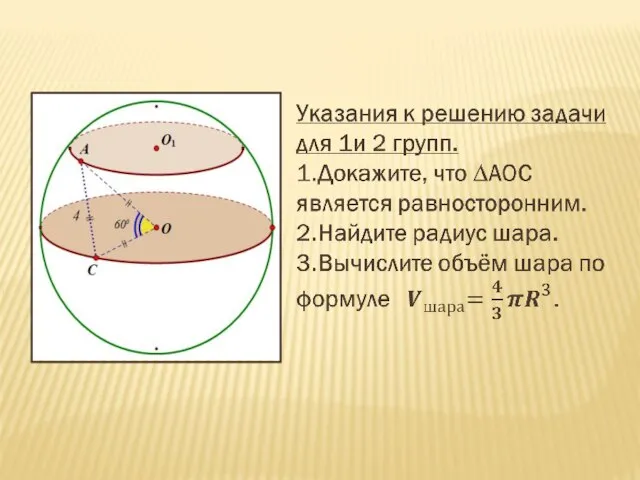
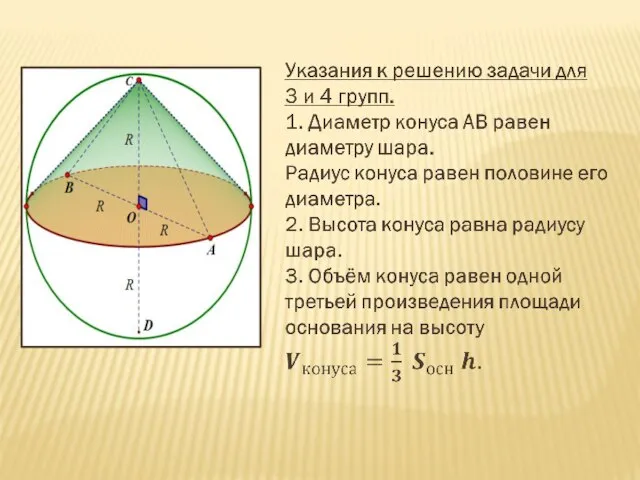
Примерный алгоритм решения задачи
1.Выполнить графическое изображение согласно
условия.
2.Выполнить на чертеже необходимые геометрические построения.
3. Провести анализ построений.
4. Произвести необходимые промежуточные
расчёты с использованием формул и теорем
планиметрии (геометрии на плоскости). Если
необходимо, применить дополнительно формулы
из стереометрии.
5. Произвести окончательные расчёты.

3. Зная катеты АВ и АС прямоугольного ∆СВА, по теореме Пифагора можно найти гипотенузу ВС.
4. Зная диаметр ВС данной сферы можно найти её радиус.

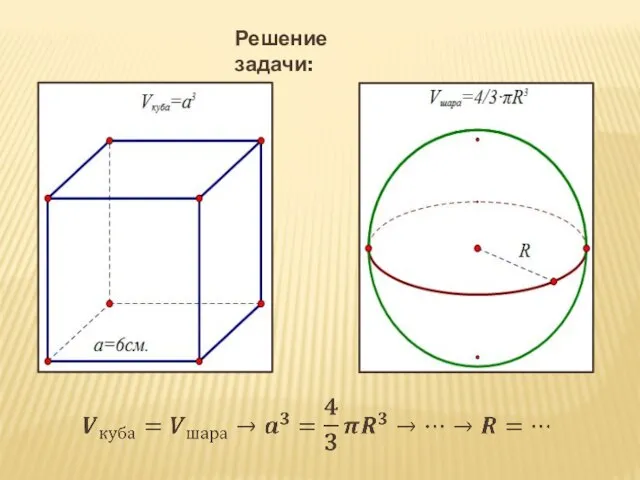
РЕШИТЕ ЗАДАЧУ САМОСТОЯТЕЛЬНО:
Стальной брусок, имеющий форму куба, переплавили в шар. Вычислите длину радиуса шара, если длина ребра бруска равна 6 см.

Решение задачи:

Решение:
Так как одна из вер­шин куба яв­ля­ет­ся цен­тром сферы с ра­ди­у­сом, мень­шим либо рав­ным сто­ро­не куба, в кубе со­дер­жит­ся 1/8 сферы и, со­от­вет­ствен­но, 1/8 ее по­верх­но­сти, рав­на
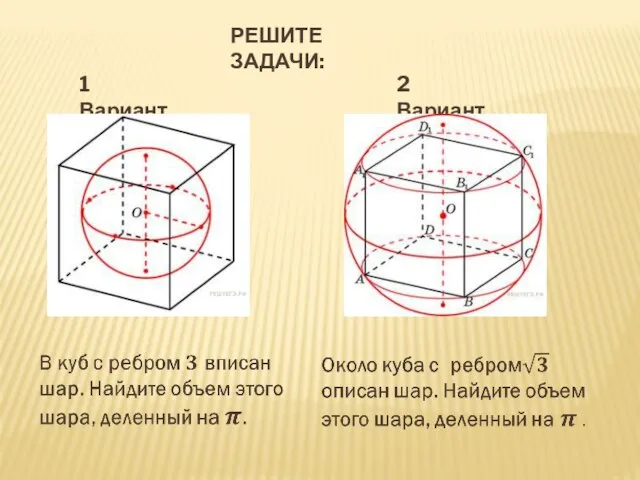
Ответ: 1,28.

РЕШИТЕ ЗАДАЧИ:
1 Вариант
2 Вариант

БЫСТРО И КРАТКО НАПИШИТЕ ОТВЕТЫ НА ВОПРОСЫ:
1. Сколько сфер можно провести: а) через одну и ту же окружность; б) через окружность и точку, не принадлежащую её плоскости?
2. Сколько сфер можно провести через четыре точки, являющиеся вершинами: а) квадрата; б) равнобедренной трапеции; в) ромба?
3. Верно ли, что через любые две точки сферы проходит один большой круг?
4. Через какие две точки сферы можно провести несколько окружностей большого круга?
5. Как должны быть расположены две равные окружности, чтобы через них могла пройти сфера того же радиуса?

ОТВЕТЫ К ВОПРОСАМ БЛИЦ - ОПРОСА:
1. а) бесконечно много; б) одну.
2. а) бесконечно много; б) бесконечно много; в) ни одной.
3. Нет.
4. Диаметрально противоположные.
5. Иметь общий центр.

ЗАДАЧИ ДЛЯ ДОМАШНЕЙ РАБОТЫ:
1. Шар с центром в точке О касается плоскости. Точка А лежит в этой плоскости. Найдите расстояние от точки А до точки касания, если её расстояние от центра шара равно 25 см, а радиус шара равен 15 см.
2. В шаре радиуса 26 см на расстоянии 10 см от центра проведена секущая плоскость. Найдите плоскость сечения.