Параллелепипед. Элементы параллелепипеда

Определение
Параллелепипед- это параллелепипед, у которого все грани прямоугольники.
- Чертёж параллелепипеда
Параллелепипед- призма, основанием которой служит параллелограмм, или многогранник, у которого шесть граней и каждая из них параллелограмм.

Элементы параллелепипеда
Основания- ABCD, А1В1С1D1, и др.
Рёбра- АА1, DD1, СС1, ВВ1.
Вершины- А,В,С,D,А1,В1,С1,D1.
Грани- АА1D1D, ВВ1С1С.
Вершины- С1 и С и др.
Высота- С1С, АА1, ВВ1, СС1.

Развернутый параллелепипед
Основание
Боковая сторона по длине
Боковая сторона по длине
Основание
Бок. сторона по ширине
Бок. сторона по ширине

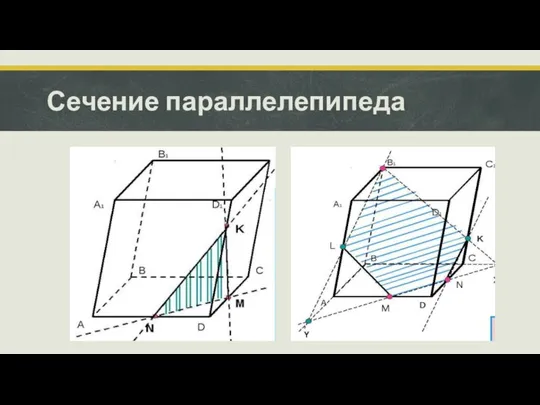
Сечение параллелепипеда

Отдельные случаи

Прямой параллелепипед
Прямой параллелепипед — это параллелепипед, у которого боковые рёбра перпендикулярны основанию.
Пример->

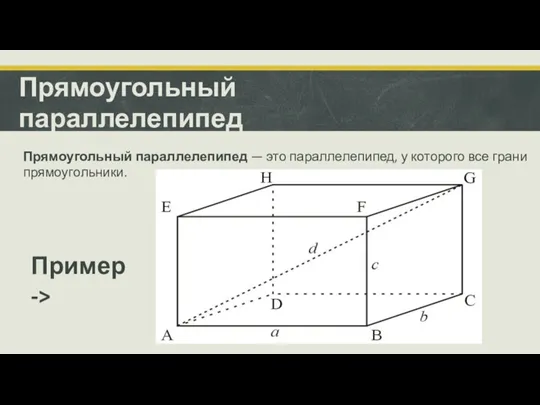
Прямоугольный параллелепипед
Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники.
Пример ->

Куб
Куб — правильный многогранник, каждая грань которого представляет собой квадрат.
- пример

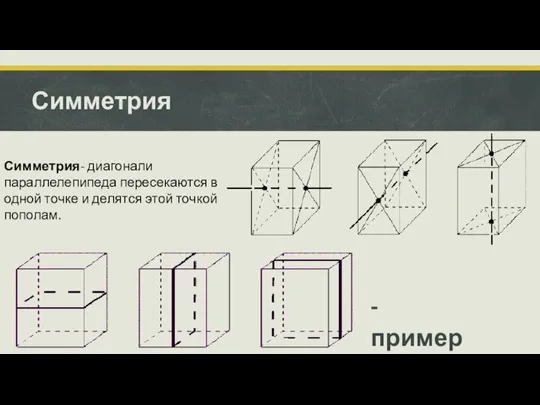
Симметрия
Симметрия- диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
- пример

Объём
V=abc

Далее