Слайд 3Первообразная (определение)
y = F(x), y = f(x), D(F) = D(f) = X,

F(x) – первообразная для f(x), если для всех x∈Х:
F′(x) = f(x).
Слайд 4Определить первообразную функции f(x) = 3x2
F(x) = x3
т.к.
F′(x) = (x3)′ =

3x2 = f(x).
Слайд 5Неопределённый интеграл
f(x) – подынтегральная функция,
f(x)dx – подынтегральное выражение.
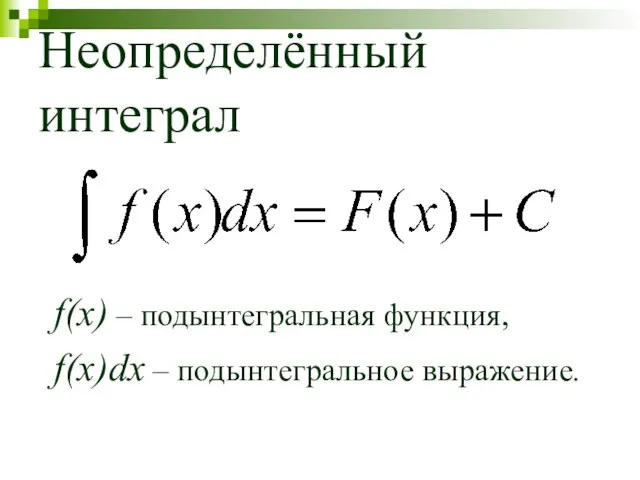
Слайд 7Занятие 1. Интеграл от степенной функции
1.
2.
3.
4.
5.
6.
7.

Слайд 8Интеграл экспоненциальной функции
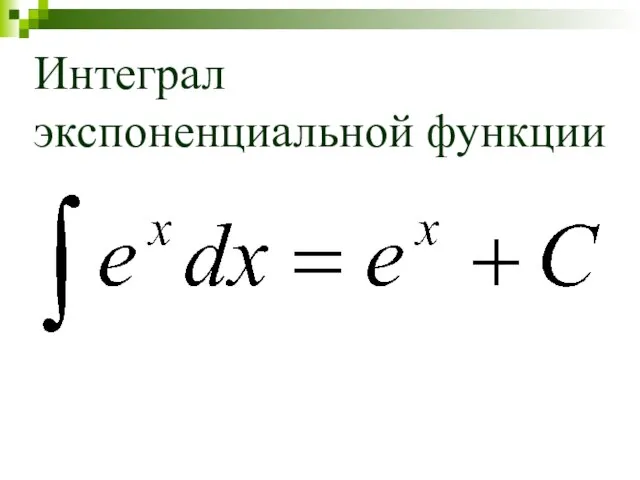
Слайд 9Интеграл
показательной функции
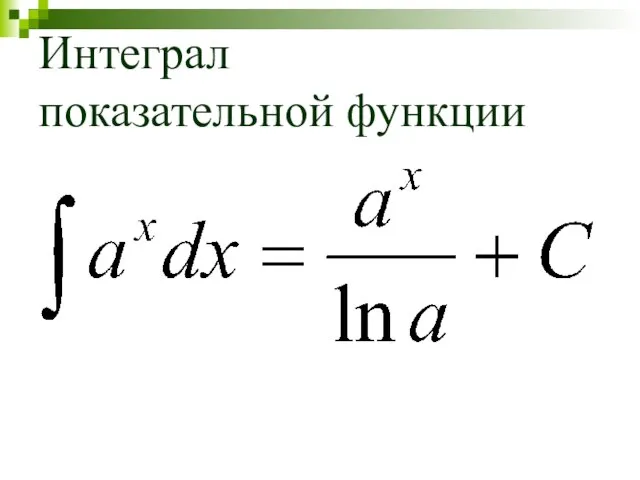
Слайд 12Непосредственное интегрирование
Найти:




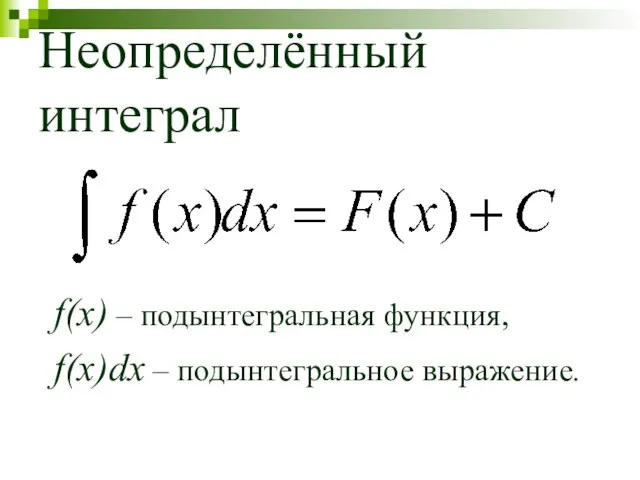
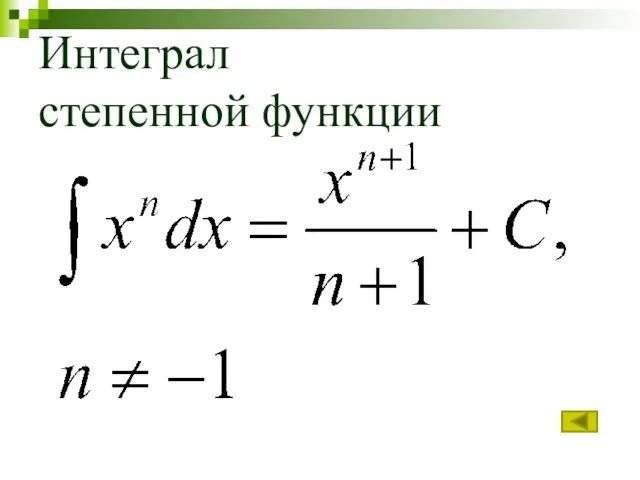

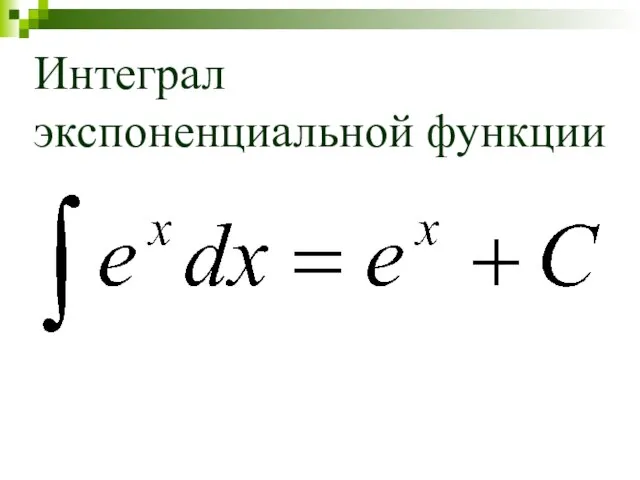
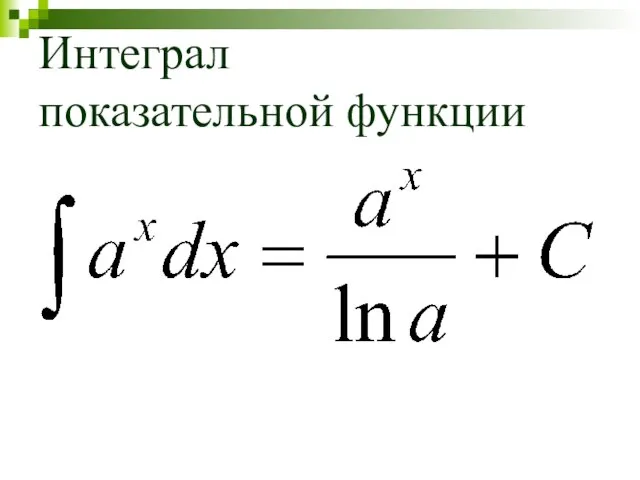

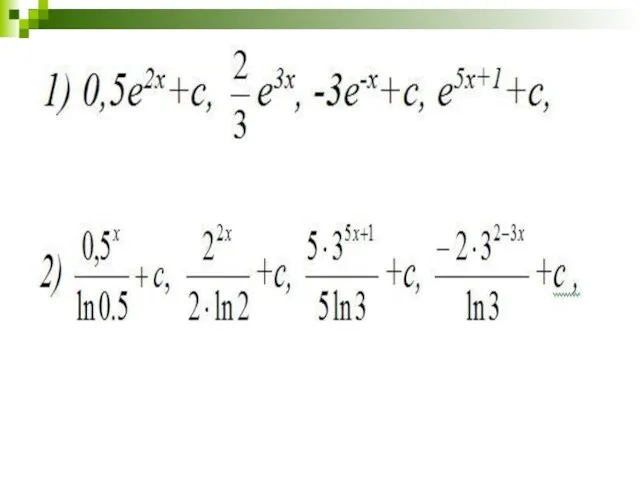

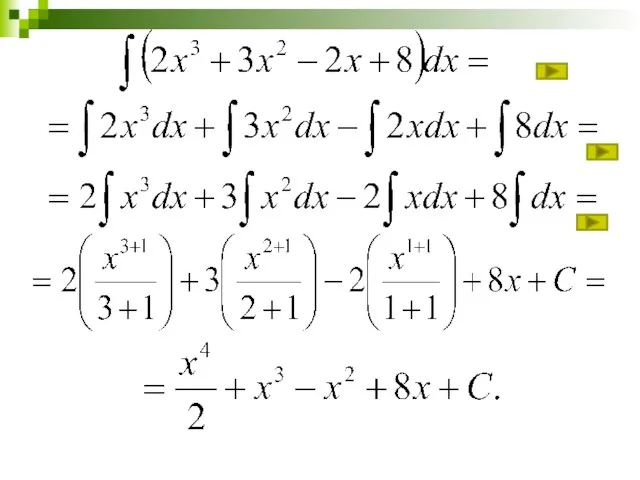
 Решите неравенства
Решите неравенства Числовые и буквенные выражения
Числовые и буквенные выражения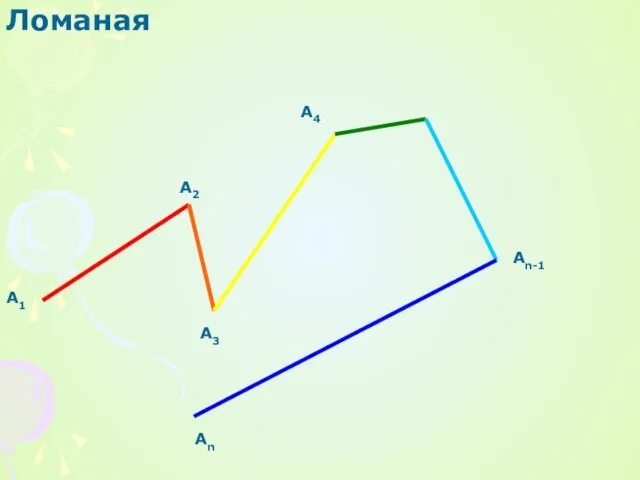 Презентация на тему Ломаная
Презентация на тему Ломаная  Первообразная. Интеграл. Площадь криволинейной трапеции
Первообразная. Интеграл. Площадь криволинейной трапеции Математическая статистика
Математическая статистика Формула Эйлера для расстояния между центрами вписанной и описанной окружностей треугольника
Формула Эйлера для расстояния между центрами вписанной и описанной окружностей треугольника Презентация на тему Целое и части (1 класс)
Презентация на тему Целое и части (1 класс)  Построение сечений
Построение сечений Aproximarea numerică a funcţiilor. Metode numerice – curs 11
Aproximarea numerică a funcţiilor. Metode numerice – curs 11 Презентация на тему КОМПЛЕКСНЫЕ ЧИСЛА
Презентация на тему КОМПЛЕКСНЫЕ ЧИСЛА  Серединный перпендикуляр
Серединный перпендикуляр Вычисление площадей фигур с помощью определенного интеграла. (Практическая работа)
Вычисление площадей фигур с помощью определенного интеграла. (Практическая работа) Сложение чисел
Сложение чисел Уравнение касательной к графику функции
Уравнение касательной к графику функции Презентация на тему Действия с векторами
Презентация на тему Действия с векторами  Площадь трапеции
Площадь трапеции Решение задач на вычисление площадей четырехугольников
Решение задач на вычисление площадей четырехугольников Презентация на тему Прикладные задачи на экстремумы
Презентация на тему Прикладные задачи на экстремумы  Величины. Свойства величин
Величины. Свойства величин Функции. ЕГЭ
Функции. ЕГЭ Многочлены. Задания
Многочлены. Задания Формулы корней квадратных уравнений
Формулы корней квадратных уравнений Понятие площади. Площадь квадрата и прямоугольника
Понятие площади. Площадь квадрата и прямоугольника Умножение. Законы умножения
Умножение. Законы умножения Презентация на тему Показательная и логарифмическая функции
Презентация на тему Показательная и логарифмическая функции  Комбинаторика. Из истории комбинаторики
Комбинаторика. Из истории комбинаторики Влияние коэффициентов квадратного трехчлена на расположение параболы
Влияние коэффициентов квадратного трехчлена на расположение параболы Пушкин и математика
Пушкин и математика