Содержание
- 2. Содержание 1. Определение касательной к графику функции. 2. Уравнение касательной к графику функции в общем виде.
- 3. Определение касательной к графику функции у=f(х) Пусть дана некоторая кривая и точка Р на ней. Возьмем
- 4. Уравнение вида у=f(a)+f’(a)(х-а) является уравнением касательной к графику функции.
- 5. Алгоритм составления касательной к графику функции у=f(x) Обозначить буквой а абсциссу точки касания. Найти f(а). Найти
- 6. Условия параллельности и перпендикулярности двух прямых. Пусть даны две прямые: у1=k1x+b1 и у2=k2x+b2. Если k1= k2,
- 7. Рассмотрим возможные типы задач на касательную
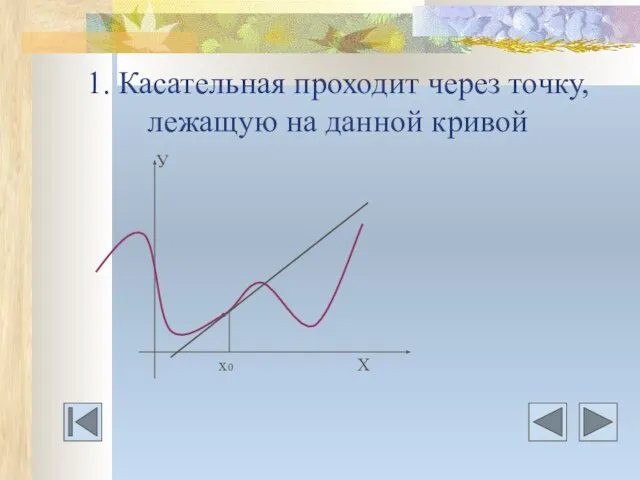
- 8. 1. Касательная проходит через точку, лежащую на данной кривой У . х0 Х
- 9. Даны дифференцируемая функция у=f(х) и 1) абсцисса точки касания; 2) ордината точки касания; 3) абсцисса точки
- 10. Решение таких задач сводится: к последовательному отысканию f(a) и f’(a); решая уравнение f(a)=у0, находим а; находим
- 11. Ключевая задача 1. Составьте уравнение касательной к графику функции у=х2–2х–3 в точке с абсциссой х0=2. Решение.
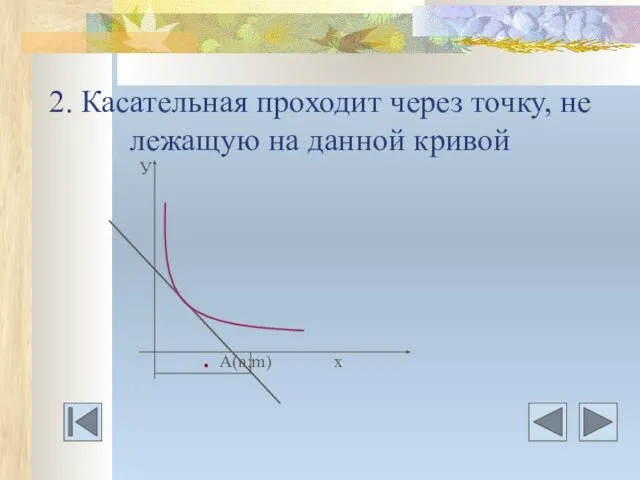
- 12. 2. Касательная проходит через точку, не лежащую на данной кривой У . A(n;m) х
- 13. Даны дифференцируемая функция у=f(х) и 1) точка А(n;m) через которую проходит касательная; 2) точка А(n;m) задана
- 14. Решение таких задач основывается на том, что координаты точки А(n;m) должны удовлетворять искомому уравнению касательной: решая
- 15. Ключевая задача 2. Напишите уравнение всех касательных к графику функции у = х2 +4х+6 проходящих через
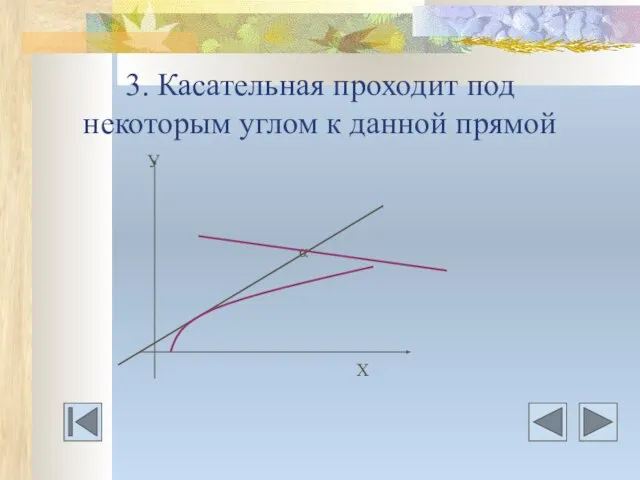
- 16. 3. Касательная проходит под некоторым углом к данной прямой У α Х
- 17. Даны дифференцируемая функция у=f(х) и 1) значение производной в точке касания f’(а); 2) указан угловой коэффициент
- 18. Решая уравнение f’(a)=k или f’(a)=tgα (если задан угол α) находим возможные значения а.
- 19. Ключевая задача 3. Напишите уравнения всех касательных к графику функции у=х2–2х–8, параллельных прямой у=-4х–4. Решение. 1.
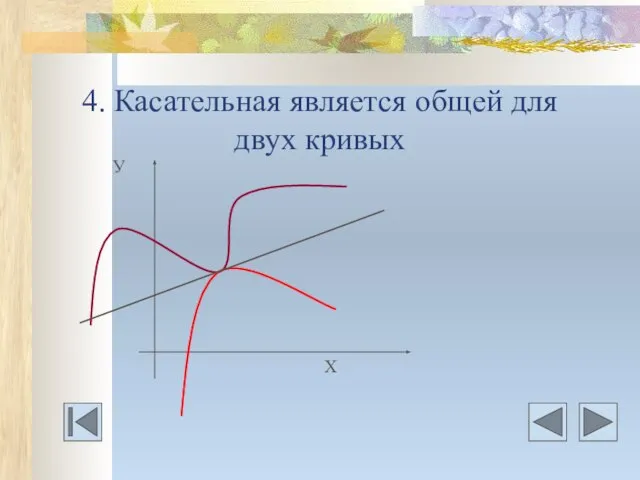
- 20. 4. Касательная является общей для двух кривых У Х
- 21. Даны дифференцируемые функция у=f(х) и y=g(x). Нужно найти уравнения общих касательных к графику этих функций.
- 22. 1 способ. Такие задачи можно решать с помощью необходимого и достаточного признака того, что прямая у=kх+b
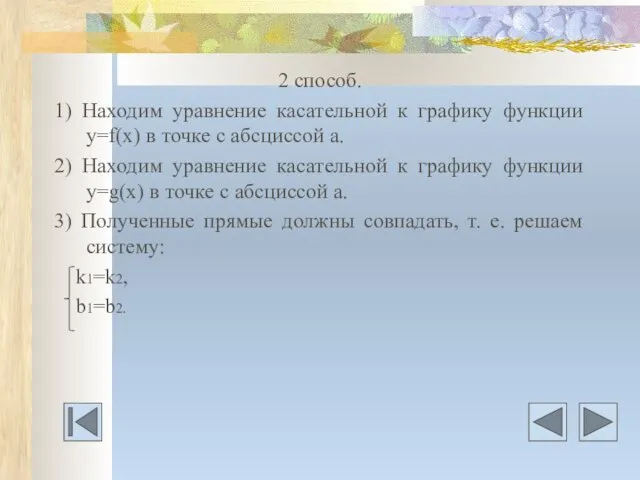
- 23. 2 способ. 1) Находим уравнение касательной к графику функции у=f(х) в точке с абсциссой а. 2)
- 24. Ключевая задача 4. Напишите уравнения всех общих касательных к графикам функций у=х2+х+1 и. у=0,5(х2+3). Решение. I
- 25. Является ли данная прямая касательной к графику функции у=f(x)? Даны дифференцируемая функция у=f(х) и уравнение прямой
- 26. 1 способ. Если у=kх+b – уравнение к графику функции в точке с абсциссой а, то f’(а)=k.
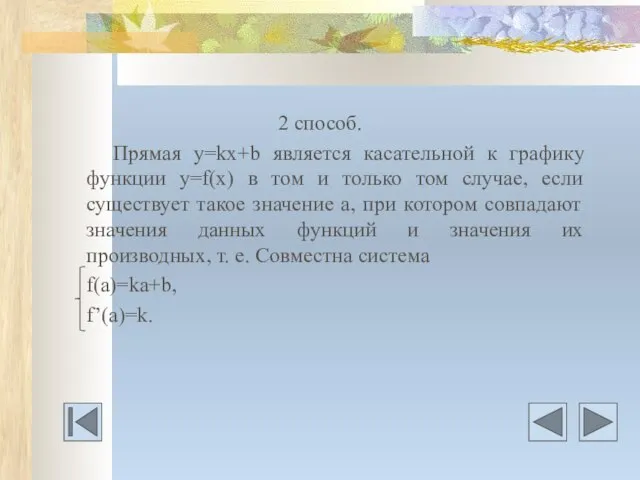
- 27. 2 способ. Прямая у=kх+b является касательной к графику функции у=f(x) в том и только том случае,
- 28. Представим разработанную систему задач в виде схемы.
- 30. Скачать презентацию





















 Параллельные прямые
Параллельные прямые Диаграммы и графики. 6 класс
Диаграммы и графики. 6 класс Математика в нашей жизни
Математика в нашей жизни Скалярное произведение векторов. Задачи
Скалярное произведение векторов. Задачи Понятие цилиндра и конуса
Понятие цилиндра и конуса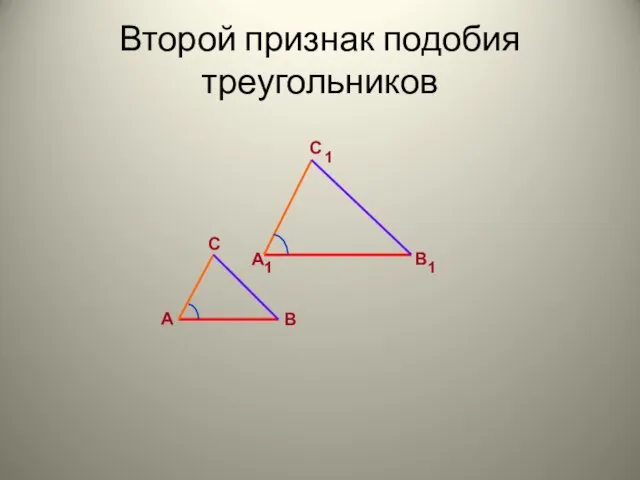 Второй признак подобия треугольников
Второй признак подобия треугольников Несократимые дроби
Несократимые дроби Тригонометрические функции, их свойства и графики
Тригонометрические функции, их свойства и графики Основы математической статистики
Основы математической статистики Различные виды тестирования при изучении темы Десятичные дроби
Различные виды тестирования при изучении темы Десятичные дроби Математика в лицах
Математика в лицах Раскрытие скобок
Раскрытие скобок Когда выполнение одного условия обеспечивает выполнение другого
Когда выполнение одного условия обеспечивает выполнение другого Устная полянка
Устная полянка Логарифмическая линия в ЕГЭ
Логарифмическая линия в ЕГЭ Справочный материал. 9 класс
Справочный материал. 9 класс Математика. Задания на лето. Часть 4
Математика. Задания на лето. Часть 4 Определенный и неопред интеграл. Тема 8
Определенный и неопред интеграл. Тема 8 Методы многокритериальной оптимизации
Методы многокритериальной оптимизации Михаил Васильевич Ломоносов. Умножение и деление степеней с натуральными показателями
Михаил Васильевич Ломоносов. Умножение и деление степеней с натуральными показателями Проверочная работа. 5 класс
Проверочная работа. 5 класс Нахождение числа по его части. (6 класс. Тест №15)
Нахождение числа по его части. (6 класс. Тест №15) Степени с рациональными показателями, их свойства
Степени с рациональными показателями, их свойства Модель плоскости
Модель плоскости Математический турнир Умники и умницы
Математический турнир Умники и умницы Геометрический и физический смысл производной, вычисление производной. 11 класс
Геометрический и физический смысл производной, вычисление производной. 11 класс Презентация на тему РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ
Презентация на тему РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ  Powtórzenie do klasówki
Powtórzenie do klasówki