Содержание
- 2. Спроби правильно відобразити на плоскому рисунку природні форми предметів були задовго до виникнення писемності – люди
- 3. Через терни до зірок. У житті нічого не дається задарма. Звичайно, якщо ви не зловили удачу
- 4. Через терни до зірок…
- 5. Працюй наполегливо, Швидко, старанно, Щоб кожна хвилина Не втратилась марно. Девіз уроку:
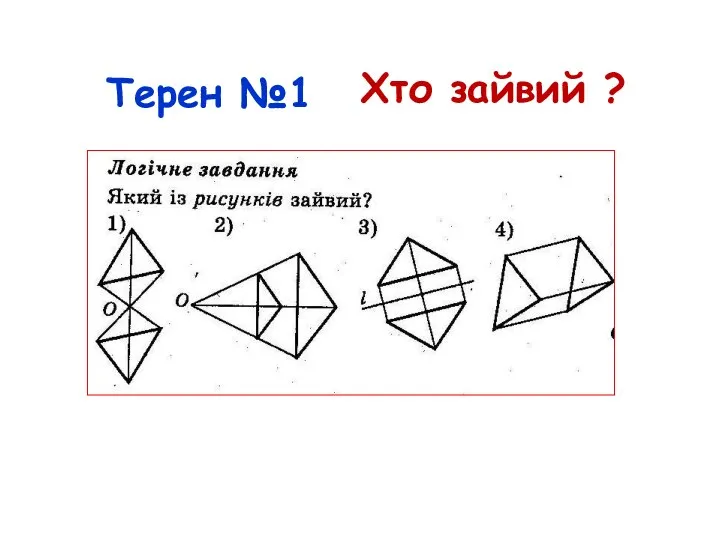
- 6. Терен №1
- 7. Терен №1 Хто зайвий ?
- 8. Терен № 2 “Згадати все”
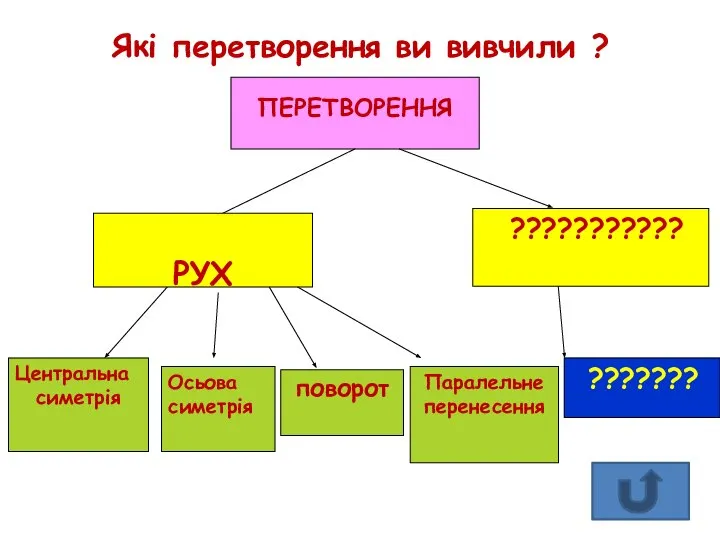
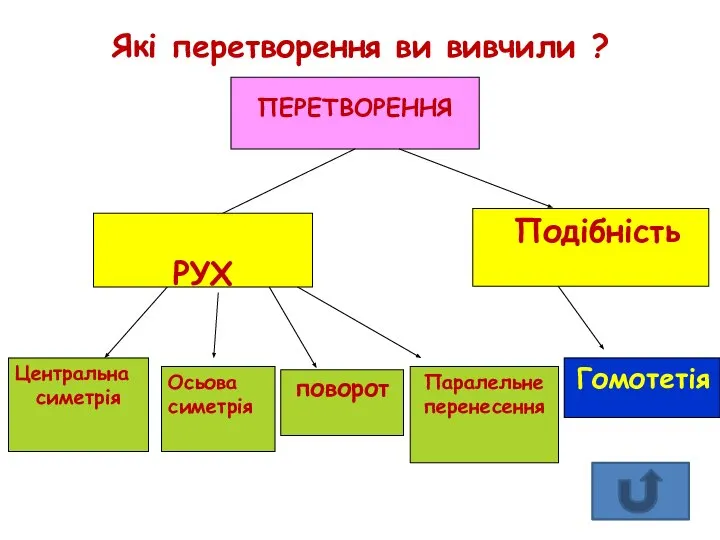
- 9. Які перетворення ви вивчили ?
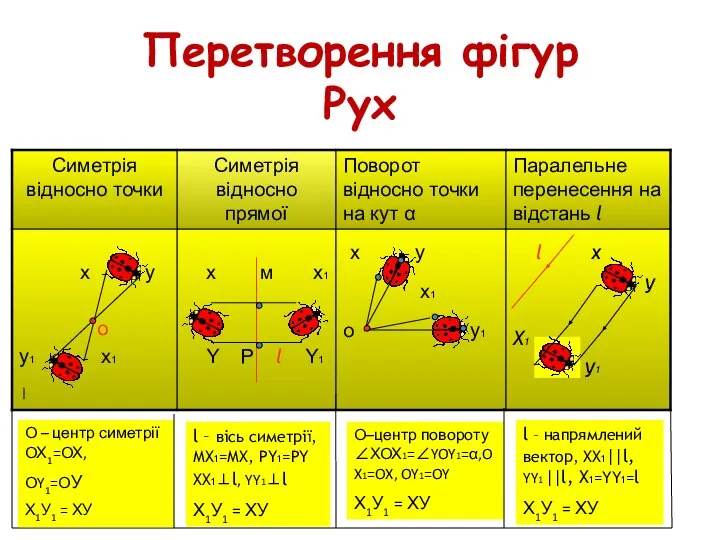
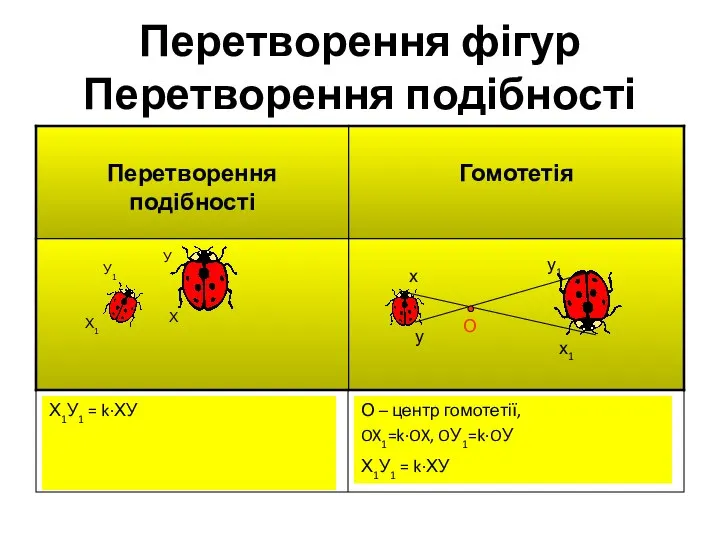
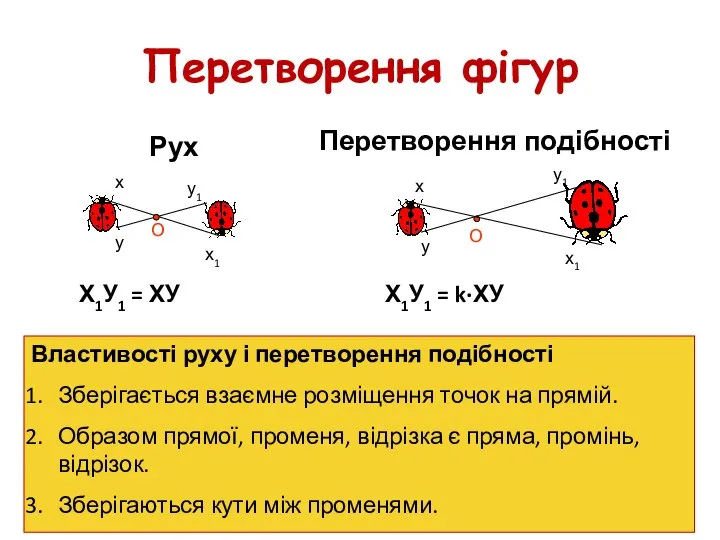
- 10. Перетворення фігур Рух О – центр симетрії ОХ1=ОХ, ОY1=ОУ Х1У1 = ХУ l – вісь симетрії,
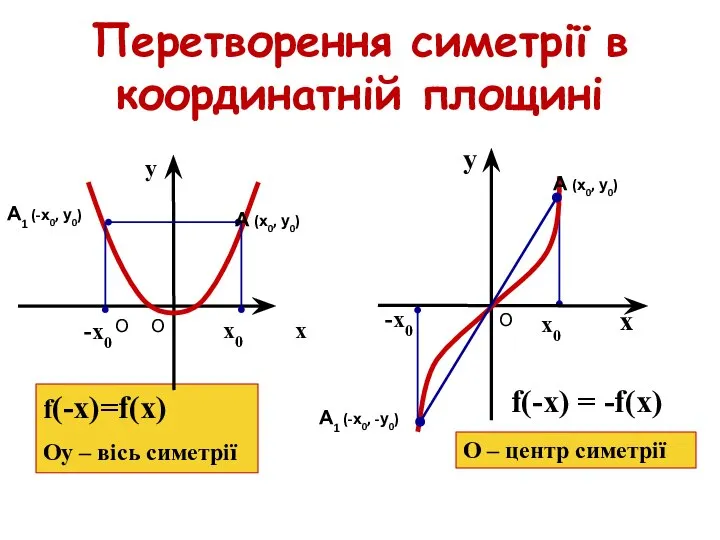
- 11. Перетворення симетрії в координатній площині f(-х)=f(x) Оу – вісь симетрії у f(-x) = -f(x) О О
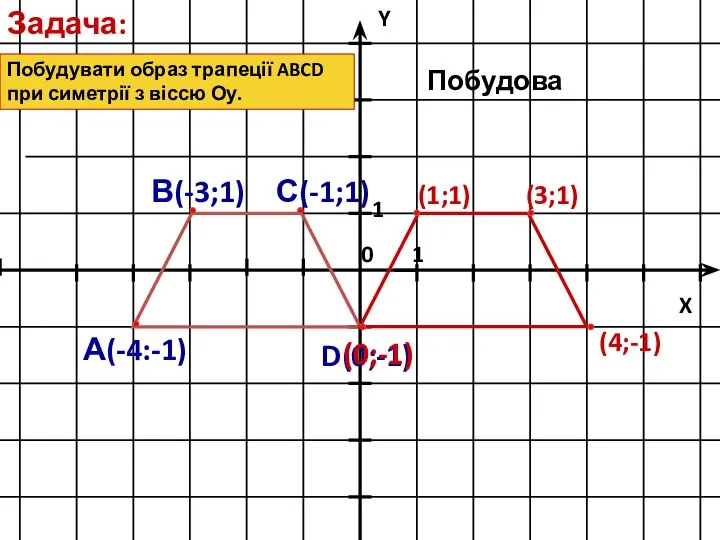
- 12. Побудувати образ трапеції ABCD при симетрії з віссю Оу. Задача: (3;1) (1;1) (0;-1) (4;-1) Побудова
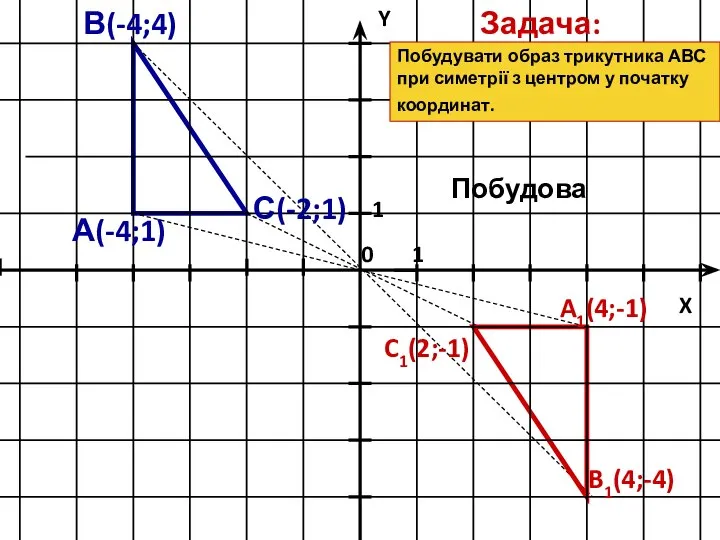
- 13. B1(4;-4) С(-2;1) A1(4;-1) C1(2;-1) А(-4;1) В(-4;4) Задача: Побудова Побудувати образ трикутника АВС при симетрії з центром
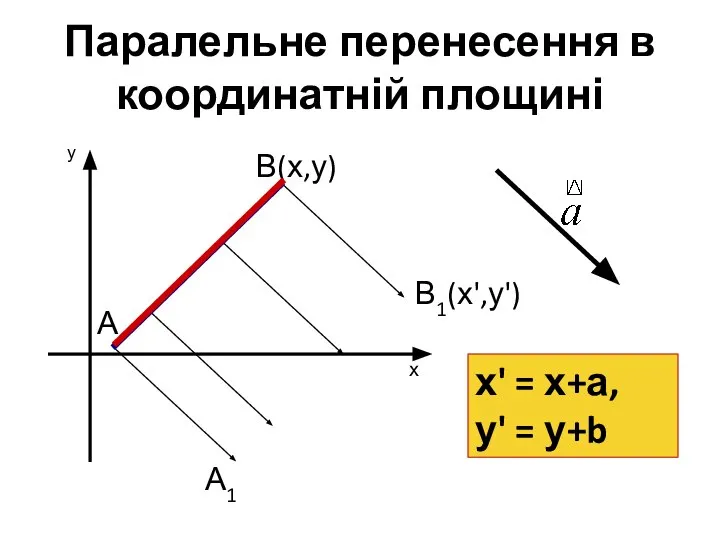
- 14. Паралельне перенесення в координатній площині А В(х,у) А1 В1(х',у') х у х' = х+а, у' =
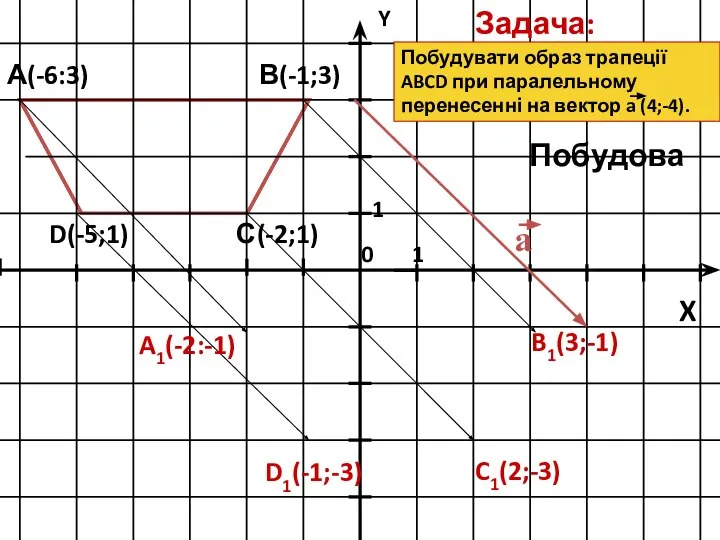
- 15. А(-6:3) В(-1;3) С(-2;1) D(-5;1) Побудувати образ трапеції ABCD при паралельному перенесенні на вектор a (4;-4). Задача:
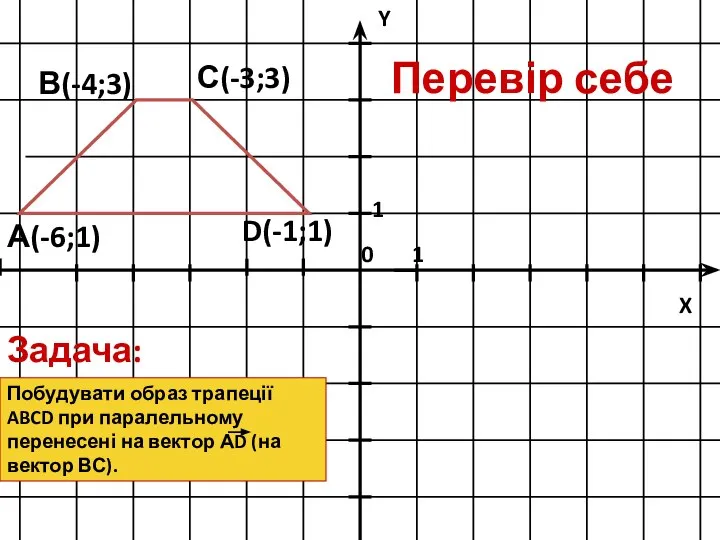
- 16. Задача: Побудувати образ трапеції ABCD при паралельному перенесені на вектор АD (на вектор ВС). А(-6;1) В(-4;3)
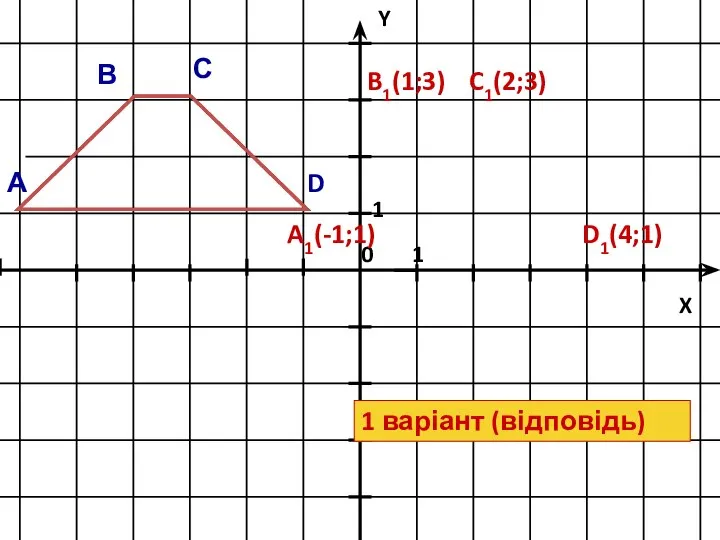
- 17. C1(2;3) D1(4;1) B1(1;3) A1(-1;1) 1 варіант (відповідь) А В С D
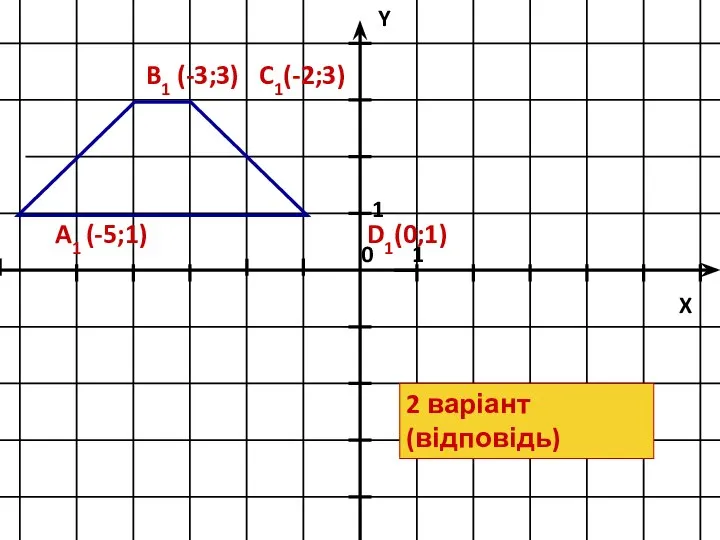
- 18. A1 (-5;1) B1 (-3;3) C1(-2;3) D1(0;1) 2 варіант (відповідь)
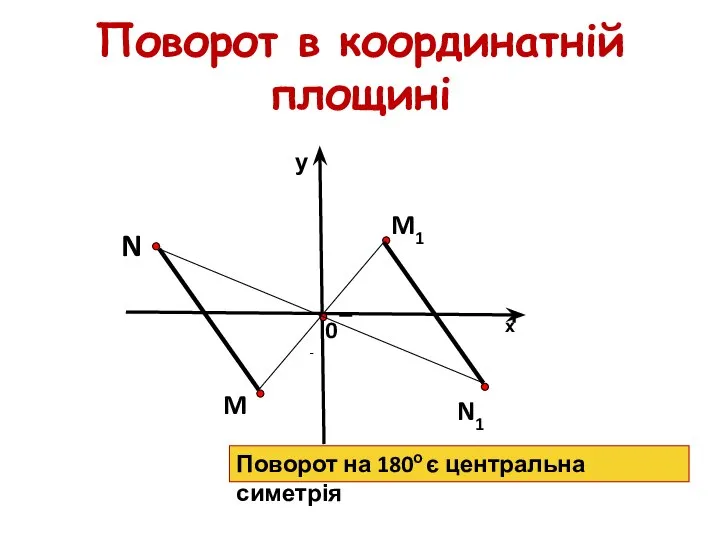
- 19. M N N1 M1 Поворот в координатній площині х у 0 Поворот на 180о є центральна
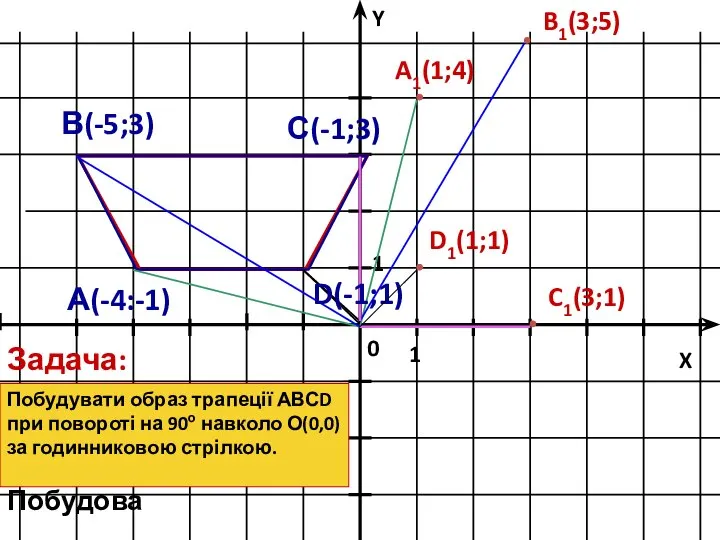
- 20. 1 1 X Y 0 А(-4:-1) В(-5;3) D(-1;1) С(-1;3) A1(1;4) B1(3;5) C1(3;1) D1(1;1) Задача: Побудувати образ
- 21. Терен №3 “Спробуй зрозумій”
- 22. Що ж таке ???????
- 23. Тема уроку: Перетворення подібності. Гомотетія
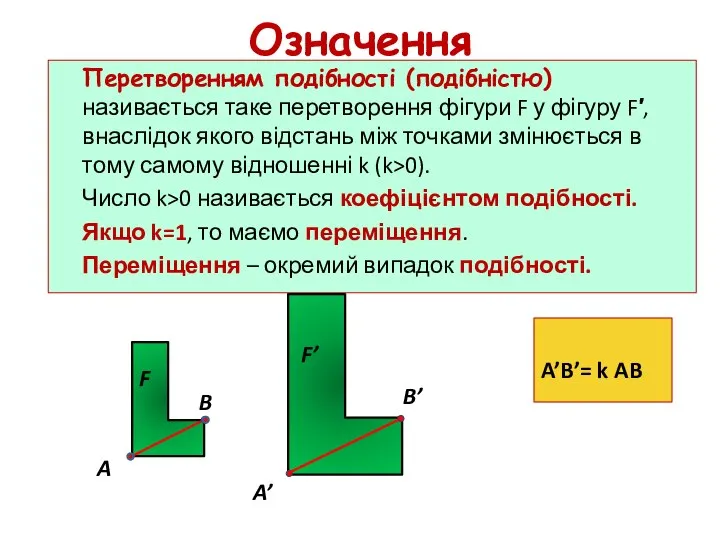
- 24. Означення Перетворенням подібності (подібністю) називається таке перетворення фігури F у фігуру F′, внаслідок якого відстань між
- 25. Які ж властивості має перетворення подібності ?
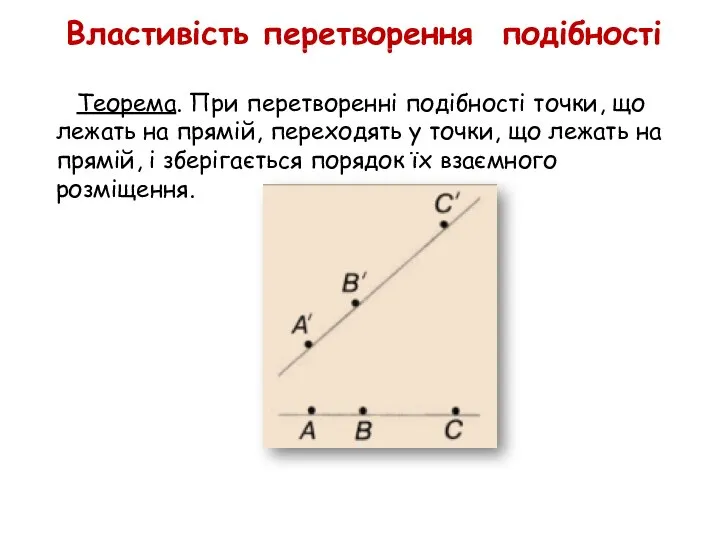
- 26. Властивість перетворення подібності Теорема. При перетворенні подібності точки, що лежать на прямій, переходять у точки, що
- 27. Властивість перетворення подібності
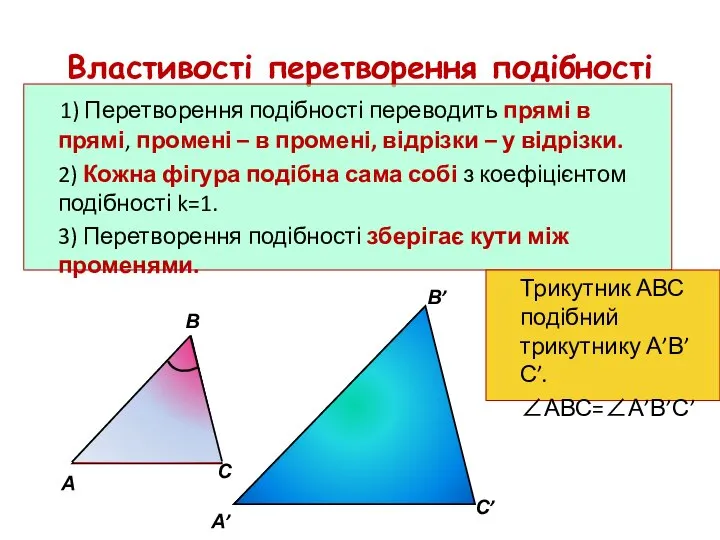
- 28. Властивості перетворення подібності 1) Перетворення подібності переводить прямі в прямі, промені – в промені, відрізки –
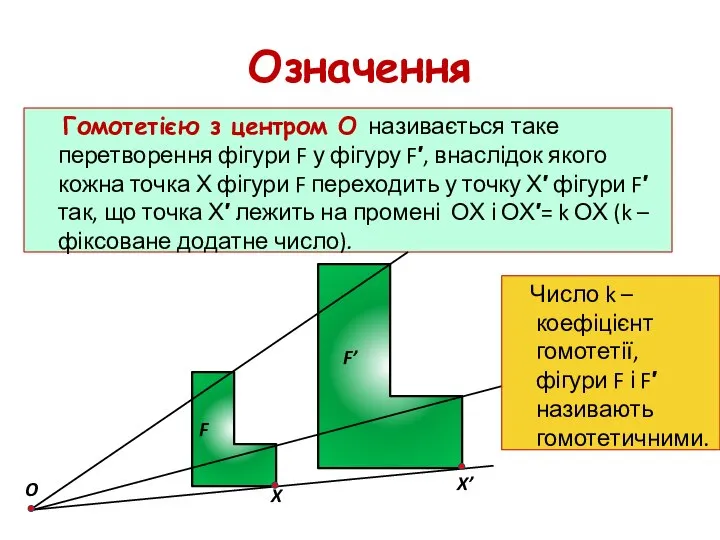
- 29. Означення Гомотетією з центром О називається таке перетворення фігури F у фігуру F′, внаслідок якого кожна
- 30. Які ж властивості має гомотетія ?
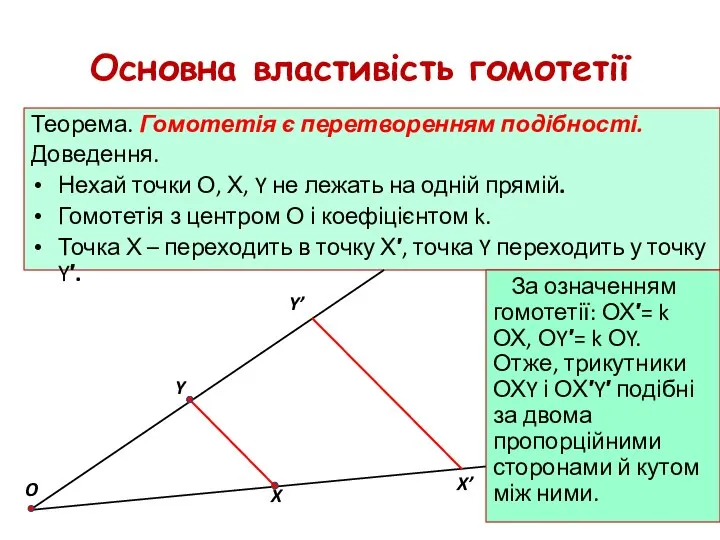
- 31. Основна властивість гомотетії Теорема. Гомотетія є перетворенням подібності. Доведення. Нехай точки О, Х, Y не лежать
- 32. Властивості гомотетії Гомотетія з коефіцієнтом k є перетворенням подібності з коефіцієнтом k. При гомотетії пряма переходить
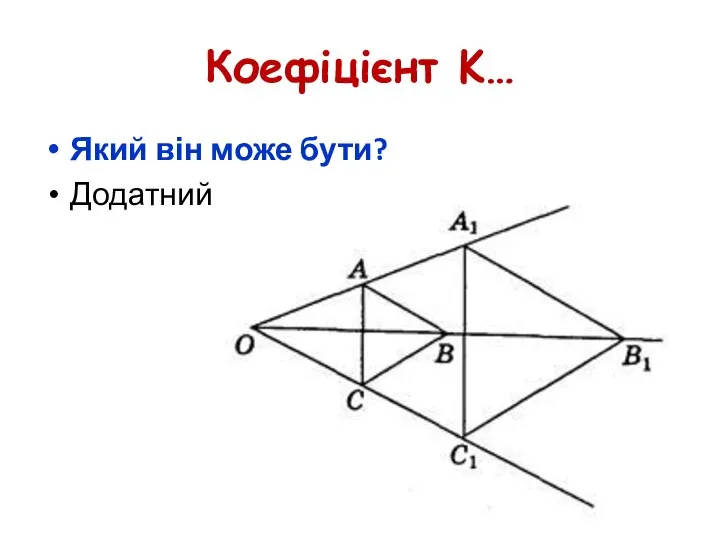
- 33. Коефіцієнт K… Який він може бути? Додатний
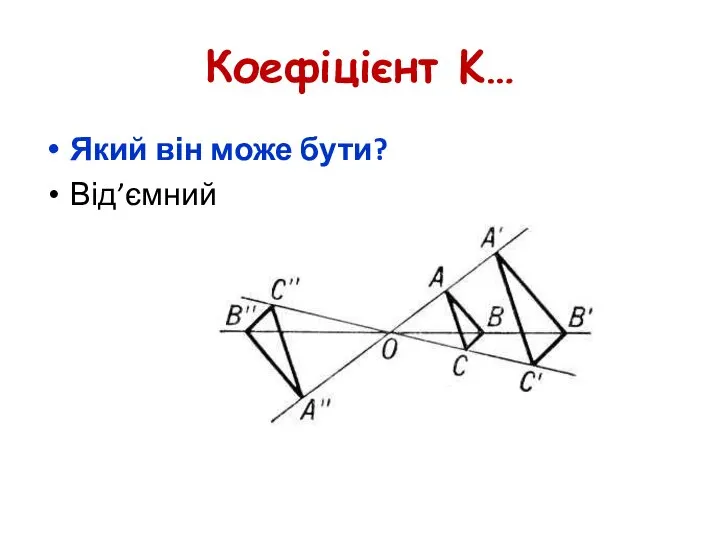
- 34. Коефіцієнт K… Який він може бути? Від’ємний
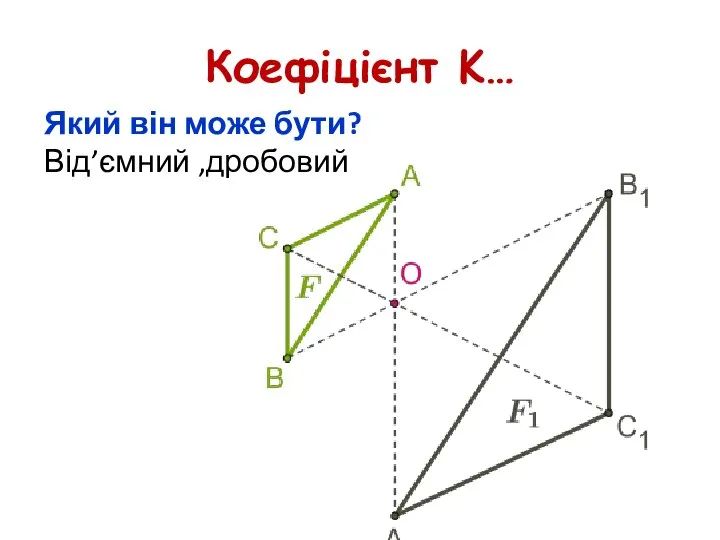
- 35. Коефіцієнт K… Який він може бути? Від’ємний ,дробовий
- 36. А як називаються фігури , що утворюються при перетвореннях подібності? Подібні
- 37. Подібні фігури Дві фігури називаються подібними, якщо вони переводяться одна в одну перетворенням подібності.
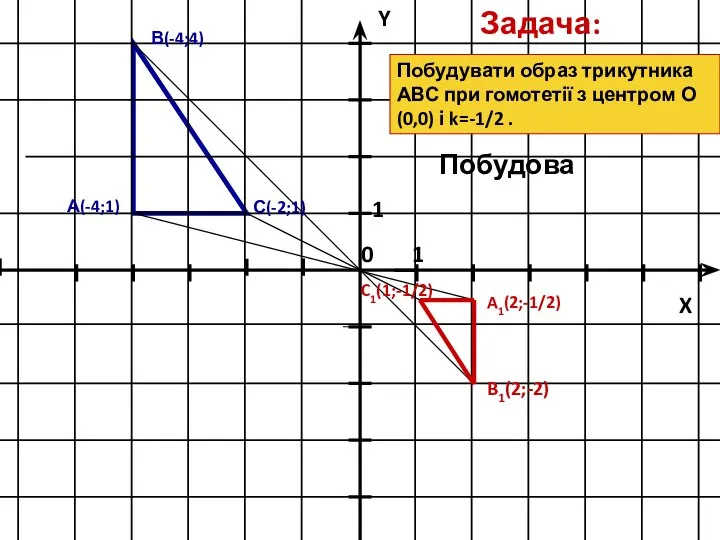
- 38. B1(2;-2) С(-2;1) A1(2;-1/2) C1(1;-1/2) А(-4;1) В(-4;4) Задача: Побудова Побудувати образ трикутника АВС при гомотетії з центром
- 39. Терен №2 Будь уважний
- 40. Історичні відомості Фігури, які мають однакову форму. Але різну величину, зустрічаються у вавілонських і єгипетських пам’ятках.
- 41. Історичні відомості Для побудови фігур, подібних до даних, є ряд практичних способів. Наприклад, для копіювання рисунків
- 42. Історичні відомості Принципом подібності користувались ще художники і скульптори стародавнього Єгипту, коли їм треба було перевести
- 43. Історичні відомості Застосовуючи поняття подібності астрономи визначали висоти місцевих гір за їх тінями. Добре відома всім
- 44. Історичні відомості Поняття подібності лежить в основі моделювання. Принцип геометричної подібності переніс на галузь фізичних явищ
- 45. Терен № 5 Знайди 10 відмінностей…
- 46. Перетворення фігур Перетворення подібності О – центр гомотетії, OX1=k·OX, OУ1=k·OУ Х1У1 = k·ХУ Х1У1 = k·ХУ
- 47. Перетворення фігур Рух Перетворення подібності х у х1 у1 О х у1 у х1 О Властивості
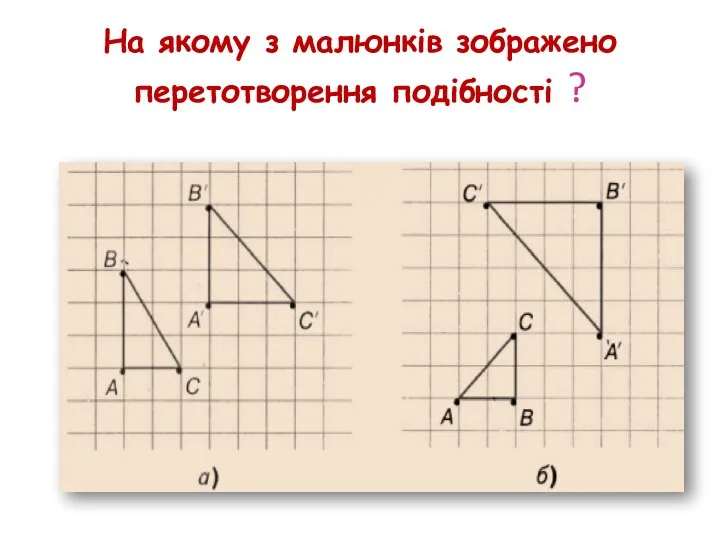
- 48. На якому з малюнків зображено перетотворення подібності ?
- 49. Будь-які дві гомотетичні фігури подібні? Будь-які дві подібні фігури гомотетичні? Чи можна вважати рівні фігури подібними?
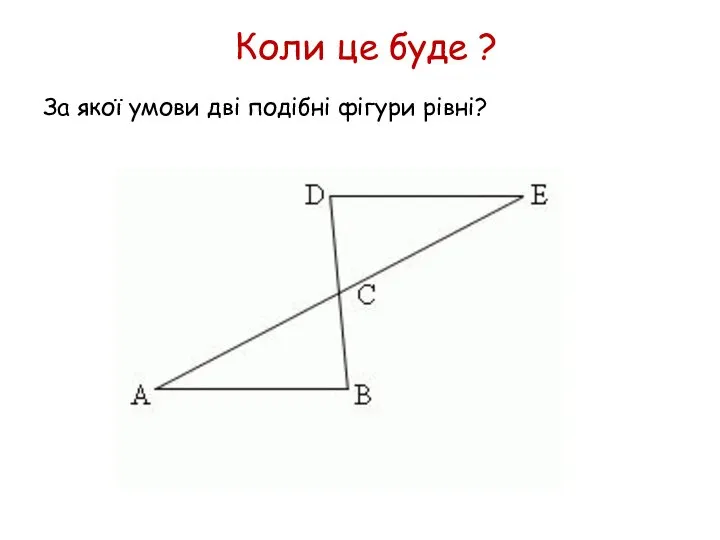
- 50. Коли це буде ? За якої умови дві подібні фігури рівні?
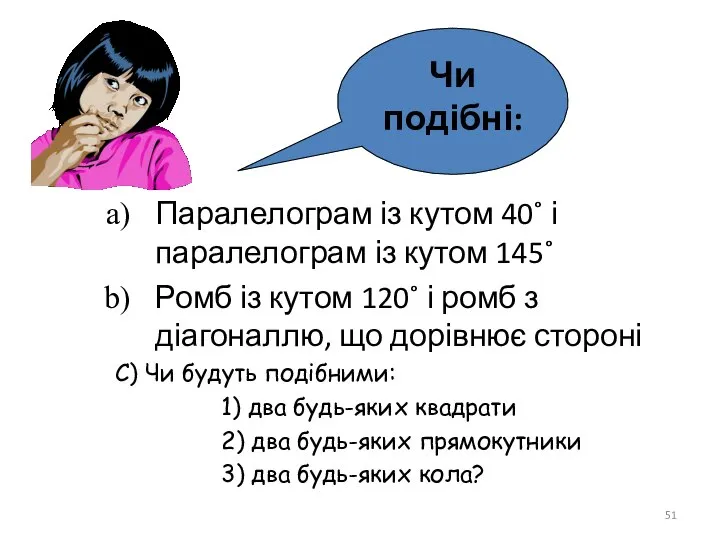
- 51. Паралелограм із кутом 40˚ і паралелограм із кутом 145˚ Ромб із кутом 120˚ і ромб з
- 52. Тренувальні вправи 1. Позначте точки О і X. Побудуйте точку X', в яку переходить точка X
- 53. Задача Знайдіть рівняння кола, в яке переходить коло х² + у² = 4 внаслідок гомотетії з
- 54. Терен № 6 Тест - драйв
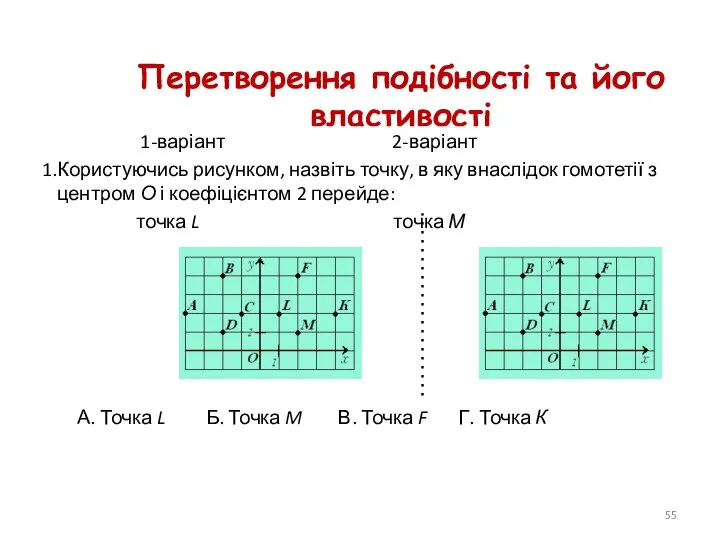
- 55. Перетворення подібності та його властивості 1-варіант 2-варіант Користуючись рисунком, назвіть точку, в яку внаслідок гомотетії з
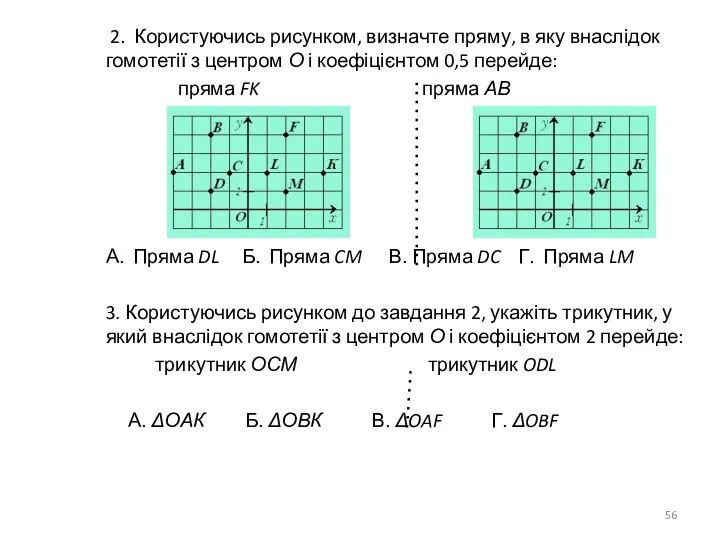
- 56. 2. Користуючись рисунком, визначте пряму, в яку внаслідок гомотетії з центром О і коефіцієнтом 0,5 перейде:
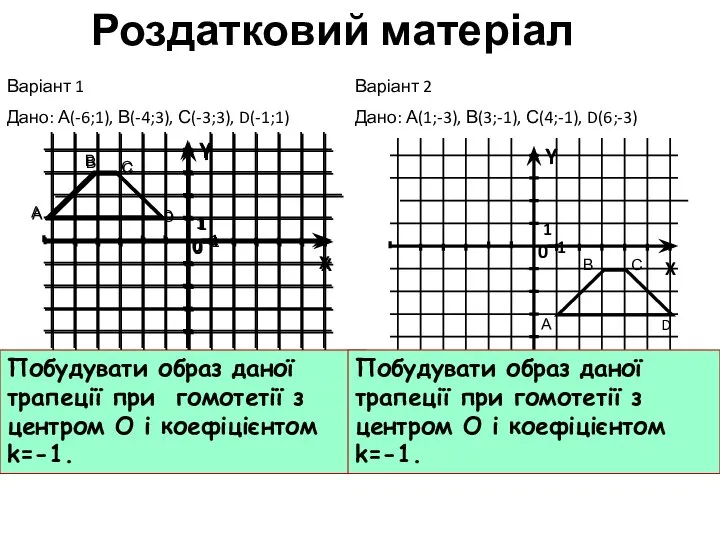
- 57. Побудувати образ даної трапеції при гомотетії з центром О і коефіцієнтом k=-1. Варіант 1 Дано: А(-6;1),
- 58. Терен № 7 Робимо висновки…
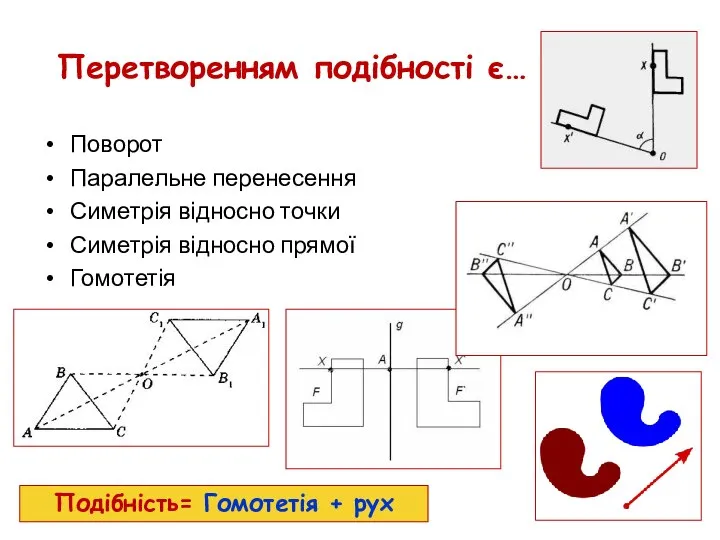
- 59. Перетворенням подібності є… Поворот Паралельне перенесення Симетрія відносно точки Симетрія відносно прямої Гомотетія Подібність= Гомотетія +
- 60. Які перетворення ви вивчили ?
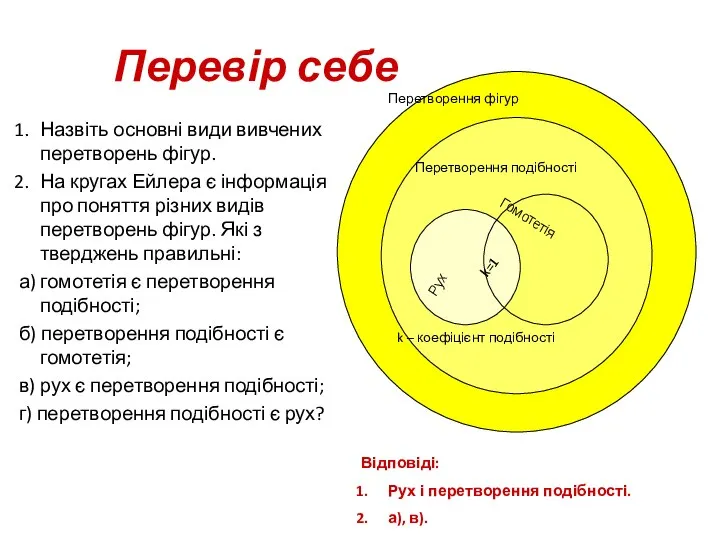
- 61. Перевір себе Назвіть основні види вивчених перетворень фігур. На кругах Ейлера є інформація про поняття різних
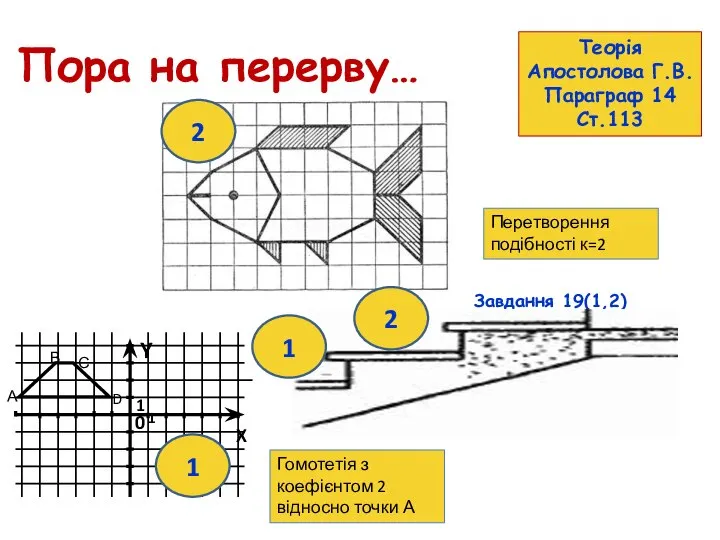
- 62. Пора на перерву… Завдання 19(1,2) ст.118 Теорія Апостолова Г.В. Параграф 14 Ст.113 2 2 1 1
- 63. Збираємо зірочки… Загадуємо бажання… Мені на згадку приходять слова відомого поета В. Симоненка: Ти знаєш, що
- 64. У Новому році бажаю: 12 місяців без хвороб 53 тижні позитиву 365 днів щастя 8760 годин
- 66. Скачать презентацию




























 Смешанные числа (часть 2)
Смешанные числа (часть 2) Презентация на тему Измерения без линейки
Презентация на тему Измерения без линейки  Экстремум функции двух переменных. Лекция №6 (УСР)
Экстремум функции двух переменных. Лекция №6 (УСР) Итоговый тест по школьному курсу Геометрия
Итоговый тест по школьному курсу Геометрия Меры длины
Меры длины Составление арифметических задач
Составление арифметических задач Пирамида и её элементы. Правильная пирамида
Пирамида и её элементы. Правильная пирамида Числовые неравенства и их свойства. Подготовка к ОГЭ
Числовые неравенства и их свойства. Подготовка к ОГЭ Реши задачу
Реши задачу Тетраэдр. Противоположные ребра
Тетраэдр. Противоположные ребра Распространение электромагнитных волн в анизотропных средах. Двойное лучепреломление в кристаллах
Распространение электромагнитных волн в анизотропных средах. Двойное лучепреломление в кристаллах Интегральное исчисление
Интегральное исчисление Геометрические тела
Геометрические тела Нахождение неизвестного вычитаемого
Нахождение неизвестного вычитаемого Зимующие птицы
Зимующие птицы Задачи на соответствие графиков формулам их задающим
Задачи на соответствие графиков формулам их задающим Решение заданий типа № 21 ОГЭ
Решение заданий типа № 21 ОГЭ Решение уравнений. Подготовка к ОГЭ
Решение уравнений. Подготовка к ОГЭ Эконометрика. Лекция 2
Эконометрика. Лекция 2 Формула Пика
Формула Пика Корень степени n
Корень степени n Определение корня n–ой степени
Определение корня n–ой степени Статистические оценки параметров распределения. Точечные и интервальные оценки
Статистические оценки параметров распределения. Точечные и интервальные оценки Алгебра. 7 класс
Алгебра. 7 класс Второй признак равенства треугольников по стороне и двум прилежащим к ней углам
Второй признак равенства треугольников по стороне и двум прилежащим к ней углам Общее решение неполного квадратного уравнения. 8 класс
Общее решение неполного квадратного уравнения. 8 класс Обратные тригонометрические функции
Обратные тригонометрические функции Занимательные математические задания
Занимательные математические задания