Содержание
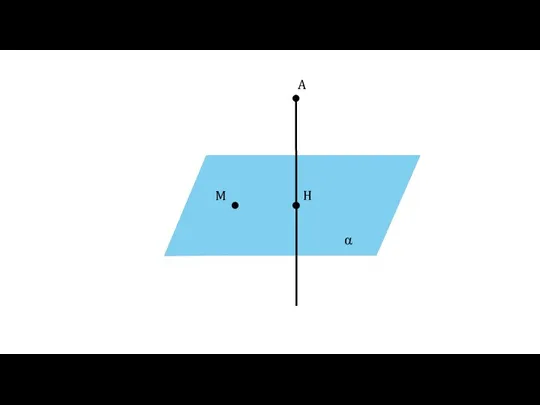
- 2. Определение Перпендикуляром, проведённым из точки А к плоскости α, называется отрезок АН. Точка Н называется основанием
- 3. α A H M
- 4. α A H M
- 5. α A H M
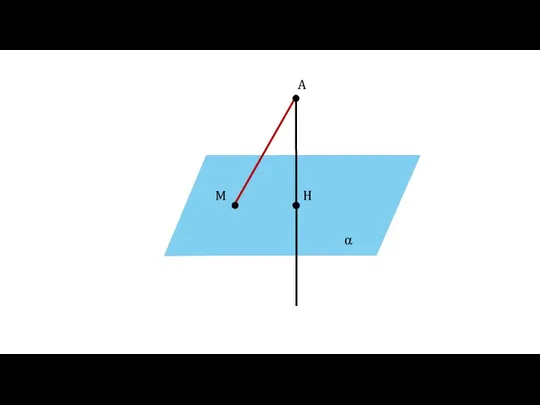
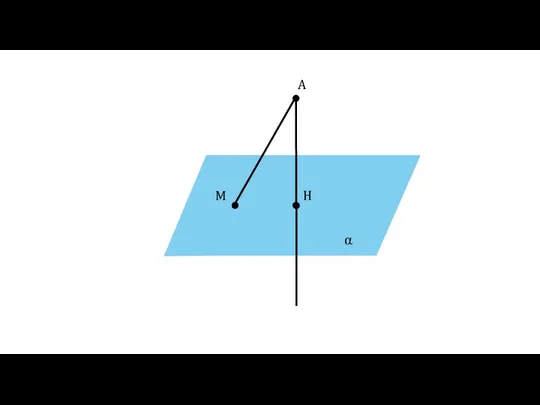
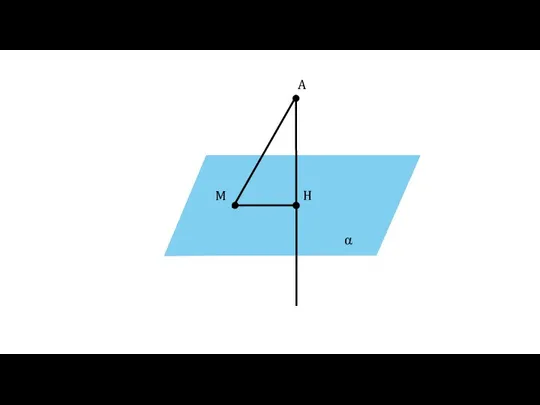
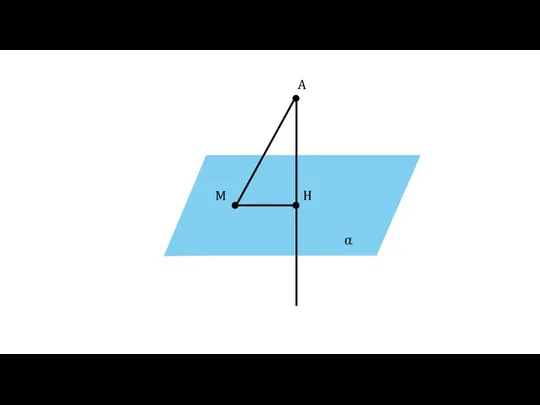
- 6. Определение Отрезок АМ называется наклонной, проведённой из точки А к плоскости α. Точка М называется основанием
- 7. α A H M
- 8. α A H M
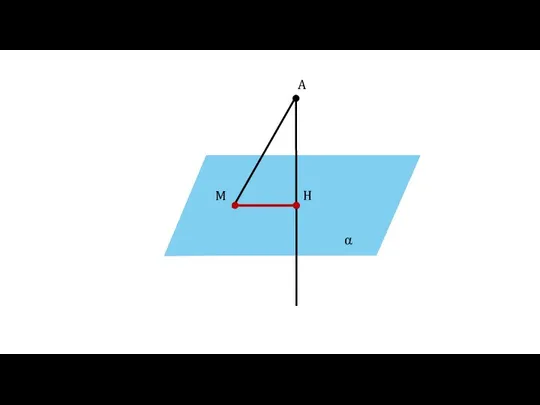
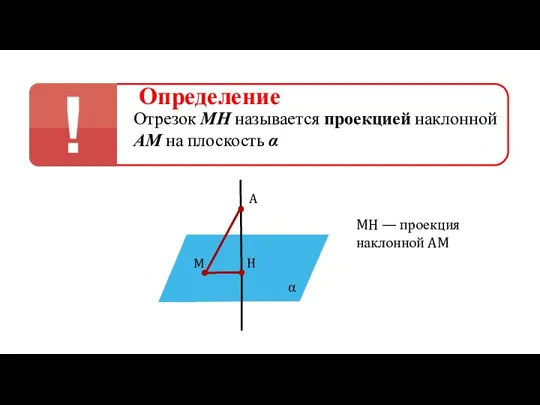
- 9. Определение Отрезок МН называется проекцией наклонной АМ на плоскость α α A H M MH —
- 10. α A H M
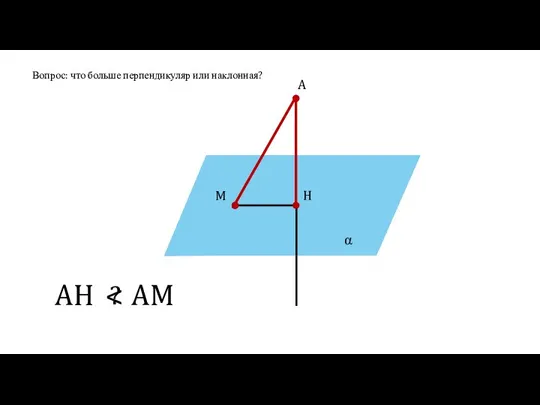
- 11. α A H M AH AM ? Вопрос: что больше перпендикуляр или наклонная?
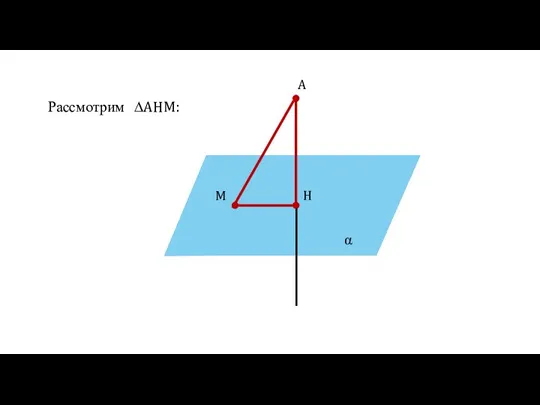
- 12. α A H M Рассмотрим ∆AHM:
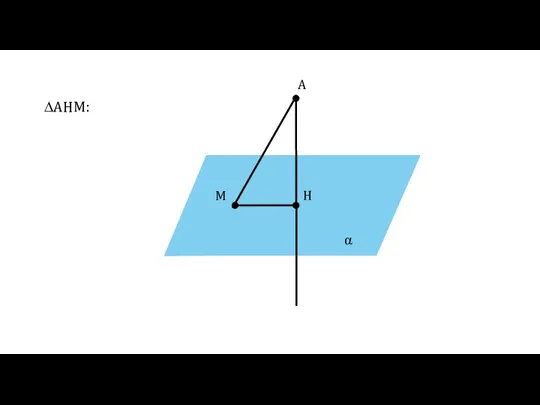
- 13. α A H M ∆AHM:
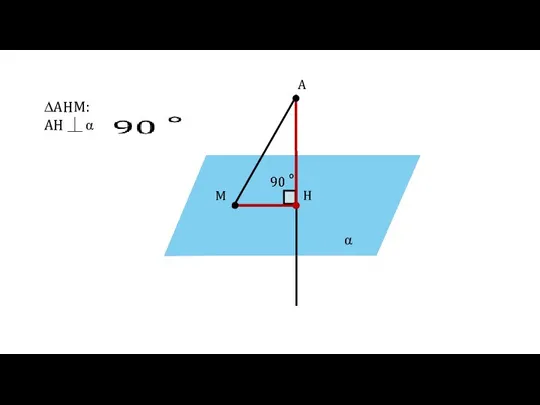
- 14. α A H M ∆AHM: AH ⏊ α
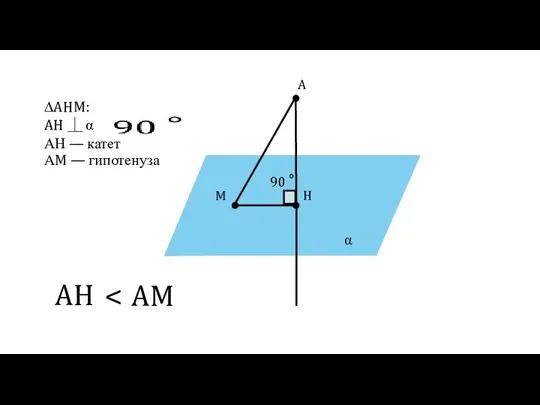
- 15. α A H M ∆AHM: AH ⏊ α AH AM АН — катет АM — гипотенуза
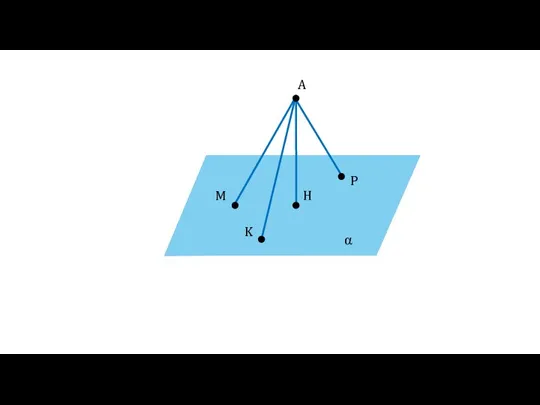
- 16. α A H M P K
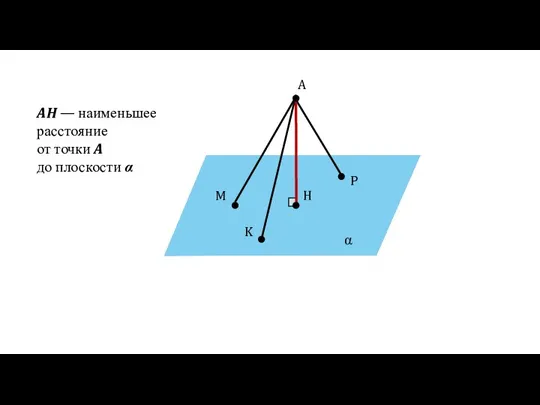
- 17. α A H M P K AH — наименьшее расстояние от точки A до плоскости α
- 18. Определение Расстоянием от точки А до плоскости α называется длина перпендикуляра АН, проведённого к плоскости α
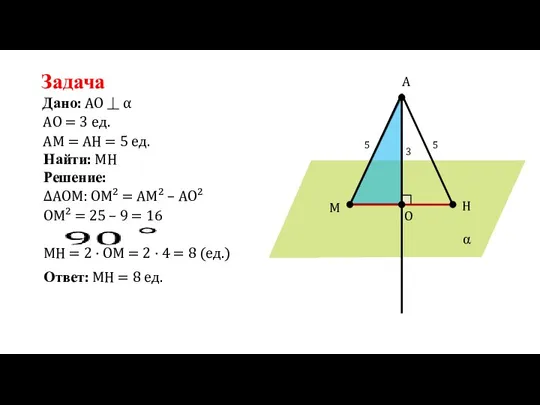
- 19. Задача Дано: AO = 3 ед. AO ⏊ α α A O M H 3 AM
- 21. Скачать презентацию



 Средняя линия треугольника
Средняя линия треугольника Презентация на тему Сложение и вычитание натуральных чисел (5 класс)
Презентация на тему Сложение и вычитание натуральных чисел (5 класс)  Векторная алгебра. Векторы на плоскости и в трехмерном пространстве, линейные операции над ними
Векторная алгебра. Векторы на плоскости и в трехмерном пространстве, линейные операции над ними Вычисление площадей плоских фигур. Трапеция
Вычисление площадей плоских фигур. Трапеция Комплексные числа
Комплексные числа Объемы многогранников и тел вращения. Практическая работа
Объемы многогранников и тел вращения. Практическая работа Координаты вектора
Координаты вектора Модели и развёртки многогранников
Модели и развёртки многогранников Теорема Пифагора. Исторический экскурс
Теорема Пифагора. Исторический экскурс Волшебный мир геометрических фигур
Волшебный мир геометрических фигур Математика в нашей жизни
Математика в нашей жизни Практико-ориентированные задания. ОГЭ, открытый банк заданий ФИПИ
Практико-ориентированные задания. ОГЭ, открытый банк заданий ФИПИ Дифференциальное исчисление элементарной и сложной функции функции
Дифференциальное исчисление элементарной и сложной функции функции Вычисление логарифмов
Вычисление логарифмов Математический биатлон
Математический биатлон Истинностные задачи
Истинностные задачи Абсолютные, относительные и средние величины. Тема 2
Абсолютные, относительные и средние величины. Тема 2 Произведение многочленов
Произведение многочленов Проценты. Примеры цепочкой
Проценты. Примеры цепочкой Функции и их графики
Функции и их графики Решение примеров
Решение примеров Прямая линия, кривая линия, отрезок, луч
Прямая линия, кривая линия, отрезок, луч Топологические опыты. Мини-урок
Топологические опыты. Мини-урок Презентация на тему Квадрат и куб числа (5 класс)
Презентация на тему Квадрат и куб числа (5 класс)  Треугольники
Треугольники Карта - схема. Бухта знаний
Карта - схема. Бухта знаний Интегралы. Введение в математический анализ
Интегралы. Введение в математический анализ Викторина по эконометрике
Викторина по эконометрике