Перпендикулярность прямых и плоскостей

Содержание
Перпендикулярность 2-х прямых
Перпендикулярность прямой и плоскости
Перпендикуляр
Наклонная
Проекция наклонной на данную плоскость
Теорема о 3-х перпендикулярах
7. Перпендикулярность 2 - х плоскостей
8. 2 свойства
Задача 1
Задача 2

ПЕРПЕНДИКУЛЯРНОСТЬ 2-Х ПРЯМЫХ.
Т1. Признак перпендикулярности
2-х прямых.
Если две пересекающиеся прямые соответственно параллельны двум перпендикулярным прямым, то эти прямые перпендикулярны
a
b
γ
Две прямые называются перпендикулярными, если все четыре угла, образовавшиеся при их пересечении, являются прямыми, т. е. равны 90° .

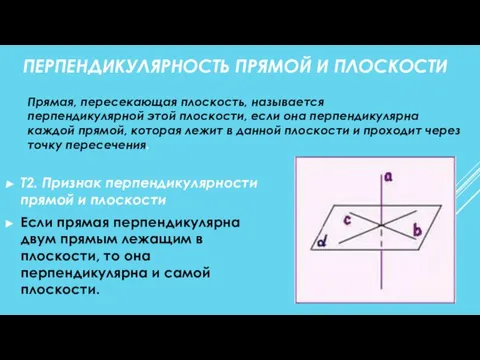
ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ
Т2. Признак перпендикулярности прямой и плоскости
Если прямая перпендикулярна двум прямым лежащим в плоскости, то она перпендикулярна и самой плоскости.
Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна каждой прямой, которая лежит в данной плоскости и проходит через точку пересечения.

ПЕРПЕНДИКУЛЯР,
НАКЛОННАЯ
И ПРОЕКЦИЯ НАКЛОННОЙ.

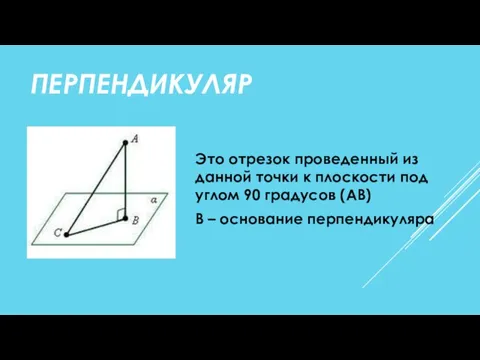
ПЕРПЕНДИКУЛЯР
Это отрезок проведенный из данной точки к плоскости под углом 90 градусов (АВ)
B – основание перпендикуляра

Это отрезок проведенный из данной точки к плоскости под углом не равным 90 градусов (АС).
С – основание наклонной.
Наклонная

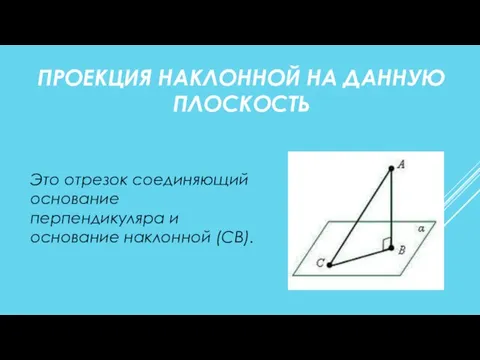
ПРОЕКЦИЯ НАКЛОННОЙ НА ДАННУЮ ПЛОСКОСТЬ
Это отрезок соединяющий основание перпендикуляра и основание наклонной (СВ).

Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной.
Т3. Теорема о 3-х перпендикулярах

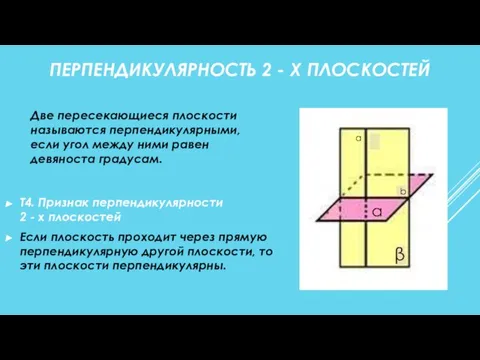
ПЕРПЕНДИКУЛЯРНОСТЬ 2 - Х ПЛОСКОСТЕЙ
Т4. Признак перпендикулярности
2 - х плоскостей
Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Две пересекающиеся плоскости называются перпендикулярными, если угол между ними равен девяноста градусам.
β
α
а
b

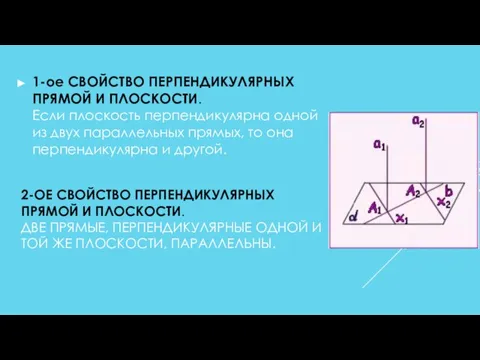
2-ОЕ СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИ.
ДВЕ ПРЯМЫЕ, ПЕРПЕНДИКУЛЯРНЫЕ ОДНОЙ И ТОЙ ЖЕ ПЛОСКОСТИ, ПАРАЛЛЕЛЬНЫ.
1-ое СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИ.
Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.

ЗАДАЧА №1. ДОКАЖИТЕ, ЧТО ЧЕРЕЗ ЛЮБУЮ ТОЧКУ ПРЯМОЙ В ПРОСТРАНСТВЕ МОЖНО ПРОВЕСТИ ПЕРПЕНДИКУЛЯРНУЮ ЕЙ ПРЯМУЮ.
Решение: пусть а - прямая и А - точка на ней. Возьмем любую точку Х вне прямой а и проведем через эту точку и прямую а плоскость . В плоскости через точку А можно провести прямую b, перпендикулярную а.