Содержание
- 2. Тема урока: «Преобразование графиков»
- 3. Рассмотрим функцию: у = 3sin(2х – π/4) + 2 Рассмотрим более простые функции: у = sin
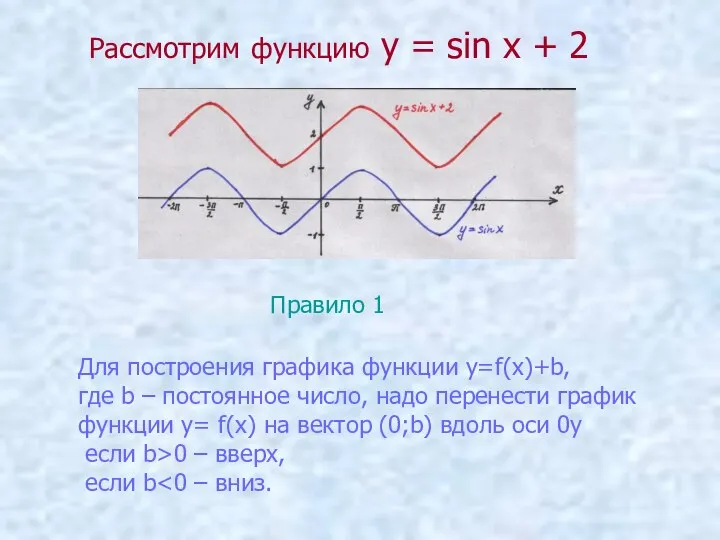
- 4. Рассмотрим функцию у = sin х + 2 Правило 1 Для построения графика функции y=f(x)+b, где
- 5. Рассмотрим функцию у = 3sin х Правило 2 Для построения графика функции y= kf(x) надо растянуть
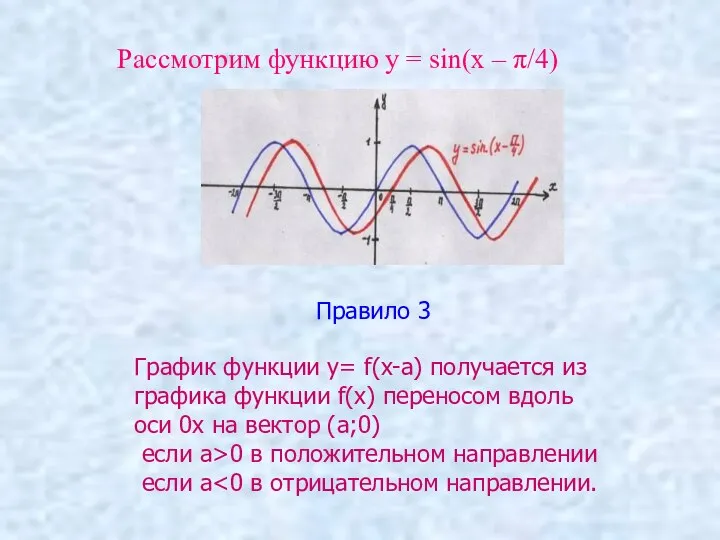
- 6. Рассмотрим функцию у = sin(х – π/4) Правило 3 График функции y= f(x-a) получается из графика
- 7. Рассмотрим функцию у = sin 2х. Правило 4 Для построения графика функции у = f(х/к) надо
- 8. Алгоритм построения графика функции у = 3sin(2х – π/4)+2 1. Постройте график функции у = sin
- 9. Задание 1. Определите, как расположены графики данных функций: у = х2 + 3, у = х3
- 10. Задание 3. Запишите вид данной функции у = 1/х, если она а) смещена на 4 единицы
- 11. Задание 5. Дайте полную характеристику данным функциям: у = 3sin(х/3 – π/3) + 4, у =
- 12. Итог урока. Правила преобразования графиков: Правило 1. Для построения графика функции y=f(x)+b, где b – постоянное
- 13. Рефлексия: · сегодня я узнал… · теперь я могу… · я почувствовал, что… · я научился…
- 15. Скачать презентацию










 Четные и нечетные функции
Четные и нечетные функции Признаки параллельности прямых
Признаки параллельности прямых Производная функции. Тест 1
Производная функции. Тест 1 Треугольник. Первый признак равенства треугольников
Треугольник. Первый признак равенства треугольников Числа-гиганты. Из истории чисел - гигантов
Числа-гиганты. Из истории чисел - гигантов Алгоритм задачи
Алгоритм задачи Формулы куба суммы и куба разности двух выражений
Формулы куба суммы и куба разности двух выражений Симметрия в пространстве
Симметрия в пространстве Цифры
Цифры Логарифмов В нашей жизни
Логарифмов В нашей жизни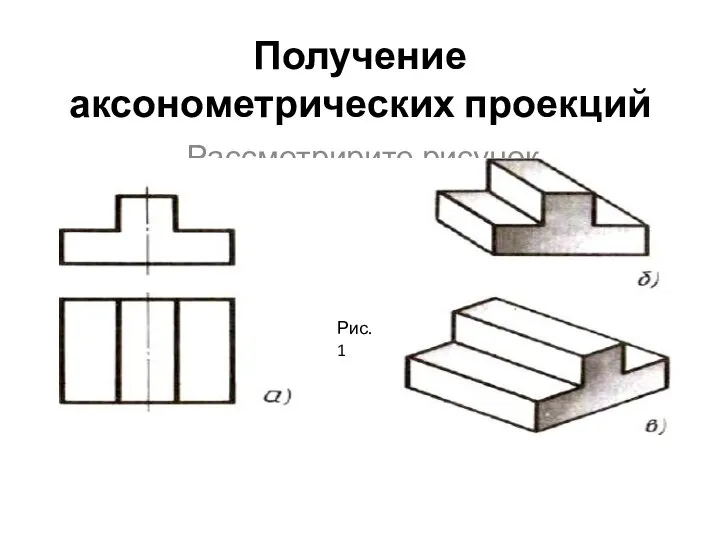 Получение аксонометрических проекций
Получение аксонометрических проекций Рефлексия. Задачи. Домашняя работа
Рефлексия. Задачи. Домашняя работа Презентация на тему Единица времени – сутки (4 класс)
Презентация на тему Единица времени – сутки (4 класс) 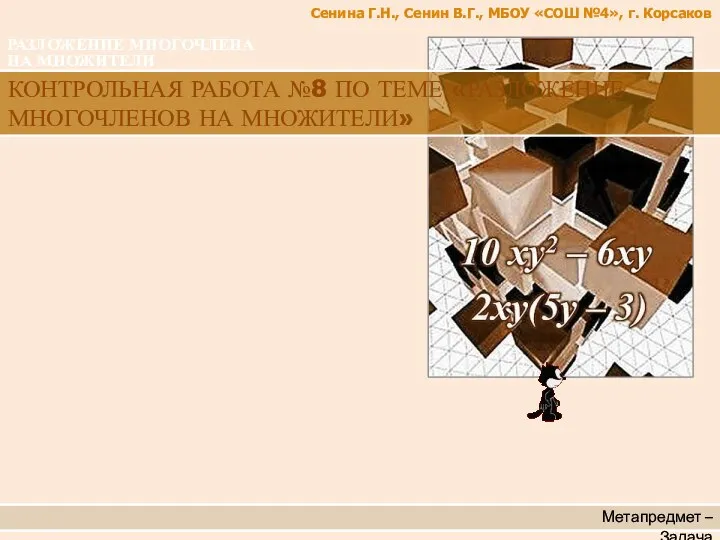 Контрольная работа №8 по теме Разложение многочленов на множители
Контрольная работа №8 по теме Разложение многочленов на множители Определить по графику
Определить по графику Векторы (понятие вектора, сложение и вычитание векторов, умножение вектора на число)
Векторы (понятие вектора, сложение и вычитание векторов, умножение вектора на число) Решение задач с помощью пропорции. 5 класс
Решение задач с помощью пропорции. 5 класс Показательные уравнения
Показательные уравнения Усеченный конус. Часть 5
Усеченный конус. Часть 5 Элементы теории вероятности
Элементы теории вероятности Разность квадратов
Разность квадратов Применение производной к построению графиков функций
Применение производной к построению графиков функций Калькуляционная карточка. Тесто заварное
Калькуляционная карточка. Тесто заварное Формулы логики
Формулы логики Ряд Тейлора функции многих переменных. Лекция 19
Ряд Тейлора функции многих переменных. Лекция 19 Построение сечений
Построение сечений Цилиндр
Цилиндр Интеллектуальная игра по математике для 8 класса
Интеллектуальная игра по математике для 8 класса