Пифагоровы тройки чисел

Теорема Пифагора применяется в геометрии на каждом шагу, она нашла широкое применение в практике и обыденной жизни. Но, кроме самой теоремы, мы изучили также и теорему, обратную к теореме Пифагора. В связи с изучением уже этой теоремы, у нас состоялось знакомство с пифагоровыми тройками чисел, т.е. с наборами из 3-х натуральных чисел a, b и c, для которых справедливо соотношение: с²=a²+b². К таким наборам относят, например, следующие тройки:
3,4,5; 5,12,13; 7,24,25; 8,15,17; 20,21,29; 9,40,41; 12,35,37
а=2kmn b=k(m²-n²) c=k(m²+n²)
Гипотеза:Проверить справедливость этих формул и найти другие, существующие формулы для вычисления пифагоровых чисел.

Объект исследования - теорема Пифагора и числа
Предмет исследования – формулы для вычисления Пифагоровых троек чисел
Методы - научного исследования, которые применялись в данной работе: анализ, сравнение, математическое вычисление.

ЦЕЛИ:
1. Найти формулы для вычисления пифагоровых троек чисел;
2. Найти количество пифагоровых троек чисел.

Задачи исследования:
Проанализировать существующие формулы для нахождения пифагоровых троек чисел;
Выявить количество пифагоровых треугольников;
Проанализировать свойства пифагоровых треугольников;
Вычислить различными способами пифагоровы тройки чисел и определить их количество;
определить типы геометрических задач, при решении которых целесообразно применение полученных формул.

Нахождение основного Пифагорова треугольника (формулы древних индусов)
Сначала докажем формулы а = 2kmn b = k(m²-n²) c = k (m²+n²),
Обозначим длины катетов через х и у, а длину гипотенузы через z. По теореме Пифагора имеем равенство: x²+y²=z²

если произведение двух взаимно простых чисел является квадратом натурального числа, то каждое из этих чисел также является квадратом натурального числа.
а =m² и b =n² , где m и n – взаимно простые числа, т.к. они являются делителями взаимно простых чисел а и b.
На основании равенства (5) имеем:
z = m²+n², x = m²-n², c² = ab = m²*n² ;
с = mn
у = 2mn.

Вывод
в каждом основном пифагоровом треугольнике хотя бы один из катетов делится на 4.
Отсюда следует, что нет пифагоровых треугольников, все стороны которого были бы простыми числами.

Пифагоровы треугольники – близнецы
три последовательных натуральных числа могут быть сторонами пифагорова треугольника только в случае египетского треугольника.
(3,4,5), (5,12,13), (7,24,25), (20,21,29), (9,40,41), (11, 60,61), (13,84,85);
число пифагоровых близнецов с гипотенузой меньшей 10, 102, 103, 104,
равно 1, 7, 24, 74 соответственно.

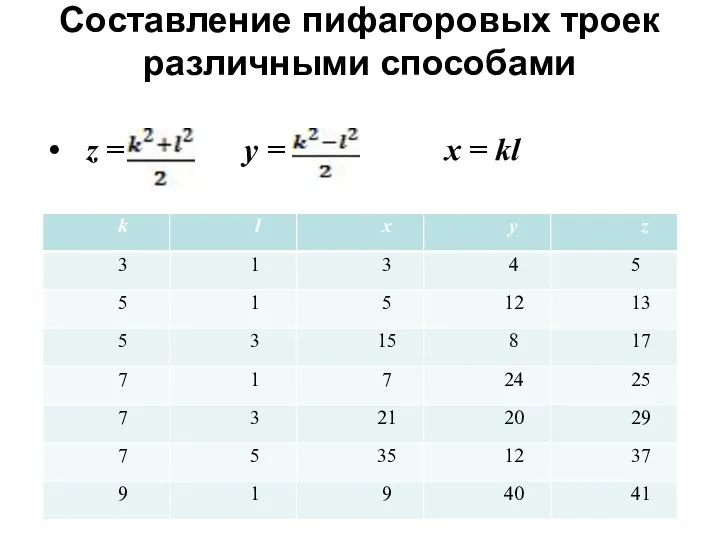
Составление пифагоровых троек различными способами
z = y = x = kl