Содержание
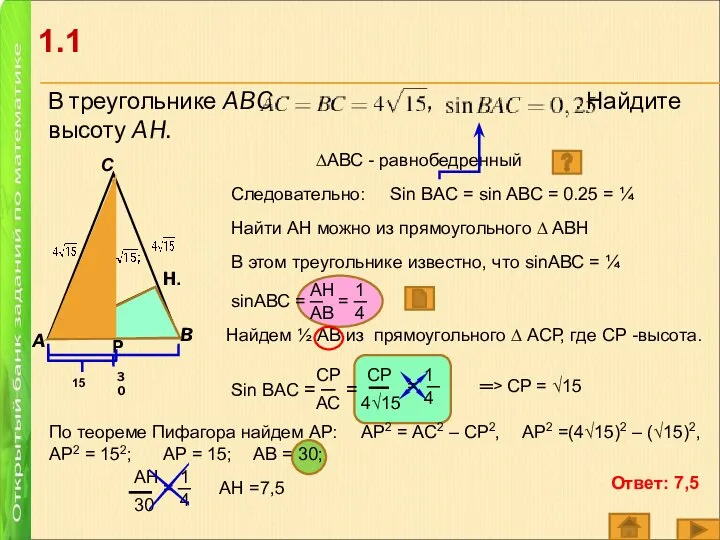
- 2. В треугольнике ABC , . Найдите высоту AH. A B Р H. 30 С ∆АВС -
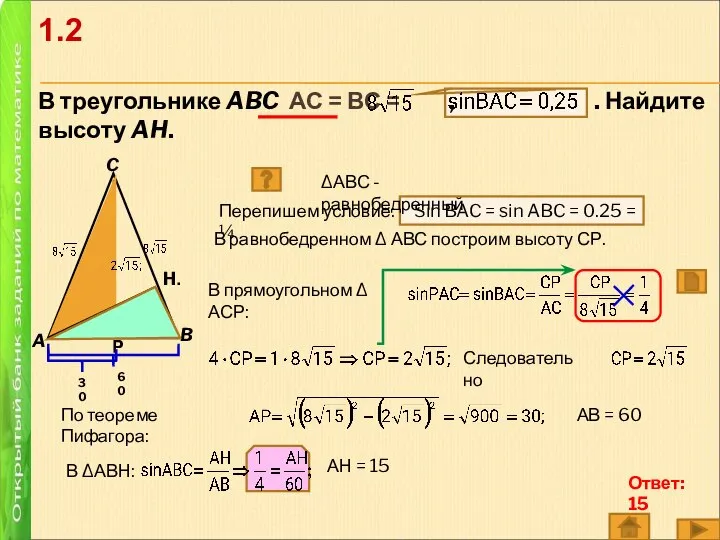
- 3. В треугольнике ABC АС = ВС = , . Найдите высоту AH. A C B Перепишем
- 4. В треугольнике ABC АС = ВС = 50, sin BAC= 0,96, Найдите высоту AH. C B
- 5. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ №1 Прямоугольный треугольник – треугольник, один из углов которого прямой. Сторона с, лежащая против
- 6. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ №2 1. В равнобедренном треугольнике углы при основании равны. 2. В равнобедренном треугольнике высота,
- 7. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ №3 Основное тригонометрическое тождество 1. 2. Формулы сокращенного умножения:
- 9. Скачать презентацию




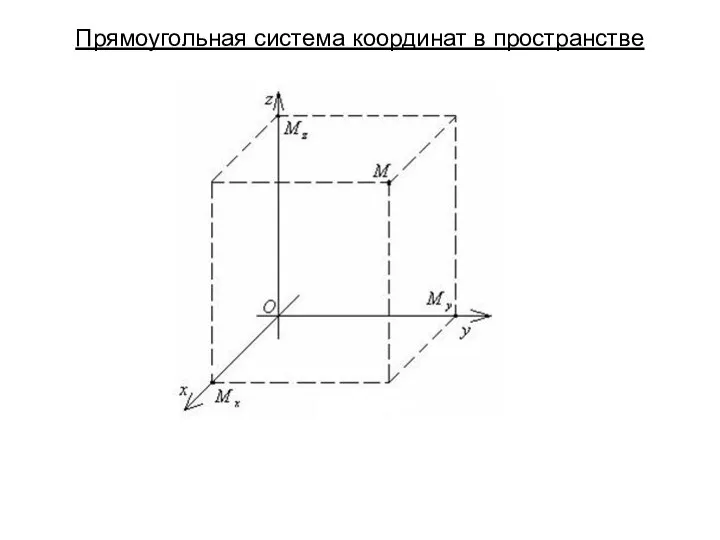 Прямоугольная система координат в пространстве. Понятие вектора
Прямоугольная система координат в пространстве. Понятие вектора Тақырып 3 Минорлар және алгебралық толықтауыштар
Тақырып 3 Минорлар және алгебралық толықтауыштар Презентация на тему Логарифмы. Применение логарифмов
Презентация на тему Логарифмы. Применение логарифмов  Презентация на тему Решение задач по математике
Презентация на тему Решение задач по математике  Призма. Площадь полной поверхности прямой призмы
Призма. Площадь полной поверхности прямой призмы Линейные однородные дифференциальные уравнения. Формула Остроградского-Лиувилля
Линейные однородные дифференциальные уравнения. Формула Остроградского-Лиувилля Многогранники, 10 класс
Многогранники, 10 класс Тригонометриялық теңдеулерді шешу тәсілдерін үйрену
Тригонометриялық теңдеулерді шешу тәсілдерін үйрену Система уравнений. Решение систем способом сложения
Система уравнений. Решение систем способом сложения Презентация по математике "Логарифмическая функция. Преобразования графиков." -
Презентация по математике "Логарифмическая функция. Преобразования графиков." -  Метод простой итерации. Метод дихотомии
Метод простой итерации. Метод дихотомии Бұрыштар
Бұрыштар Параллельность плоскостей
Параллельность плоскостей Системы линейных уравнений
Системы линейных уравнений Теорема Виета. Урок систематизации, обобщения и контроля знаний
Теорема Виета. Урок систематизации, обобщения и контроля знаний Рисуем по координатам
Рисуем по координатам Призма. Пирамида
Призма. Пирамида Коллинеарные и неколлинеарные векторы. Разложение вектора по неколлинеарным векторам
Коллинеарные и неколлинеарные векторы. Разложение вектора по неколлинеарным векторам Презентация на тему Формирование и развитие УУД на уроках математики
Презентация на тему Формирование и развитие УУД на уроках математики  Урок математики 9 класс учитель Курохтина В.А. МОУ СОШ № 1 г. Пыть-Ях
Урок математики 9 класс учитель Курохтина В.А. МОУ СОШ № 1 г. Пыть-Ях Логика и компьютер. Логические операции. Диаграммы Эйлера-Венна
Логика и компьютер. Логические операции. Диаграммы Эйлера-Венна Нечеткие числа
Нечеткие числа Деление дробей. Делимое. Взаимо обратные
Деление дробей. Делимое. Взаимо обратные Решение задач на вычисление площадей фигур
Решение задач на вычисление площадей фигур Копейка рубль бережет
Копейка рубль бережет Аналитикалық геометрия
Аналитикалық геометрия Применение производной функции для отыскания точек экстремума
Применение производной функции для отыскания точек экстремума Положительные и отрицательные числа. Диагностика
Положительные и отрицательные числа. Диагностика