Содержание
- 2. Какой четырёхугольник имеет наибольшую площадь?
- 3. Гипотеза Мы считаем, что площадь четырёхуольника зависит от длин сторон, от величин углов и от формы
- 4. Цель: Исследовать зависимость площади четырёхугольника от размеров его элементов. Задачи: 1. Изучить зависимость площади четырёхугольника от
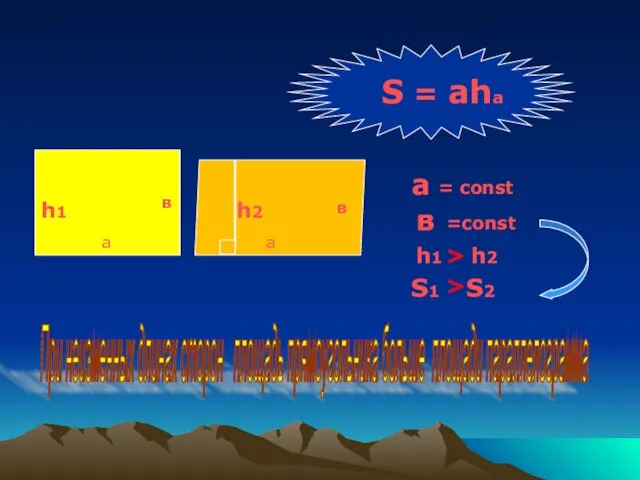
- 5. S = aha a в = const =const При неизменных длинах сторон площадь прямоугольника больше площади
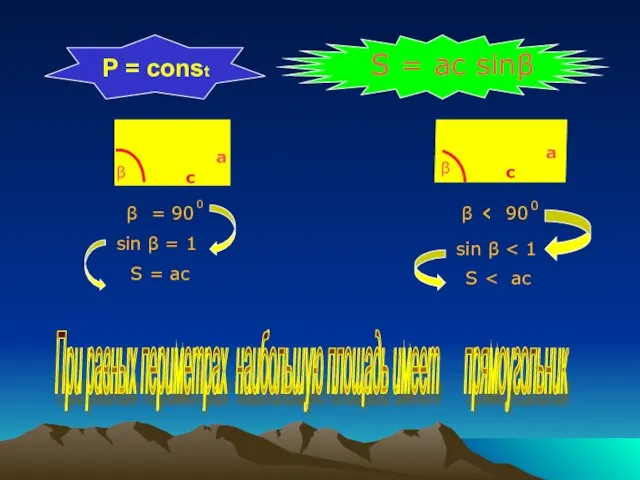
- 6. S = ac sinβ β β ‹ = 90 0 90 0 sin β = 1
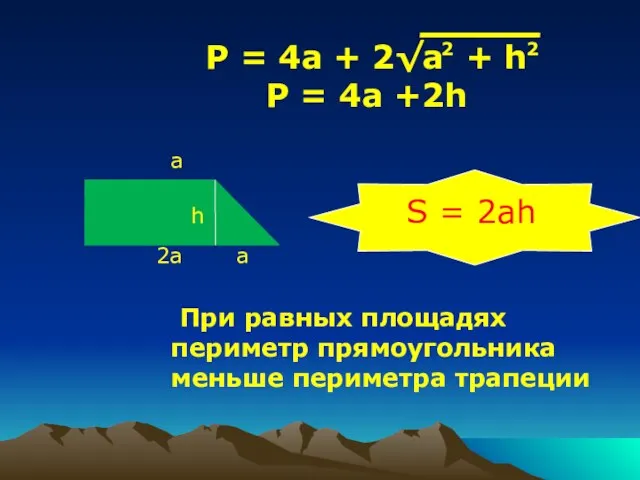
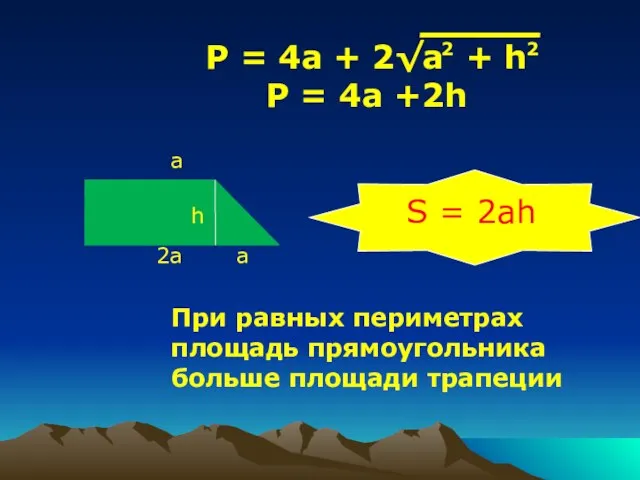
- 7. h 2a a a P = 4a + 2√a + h P = 4a +2h S
- 8. h 2a a a P = 4a + 2√a + h P = 4a +2h S
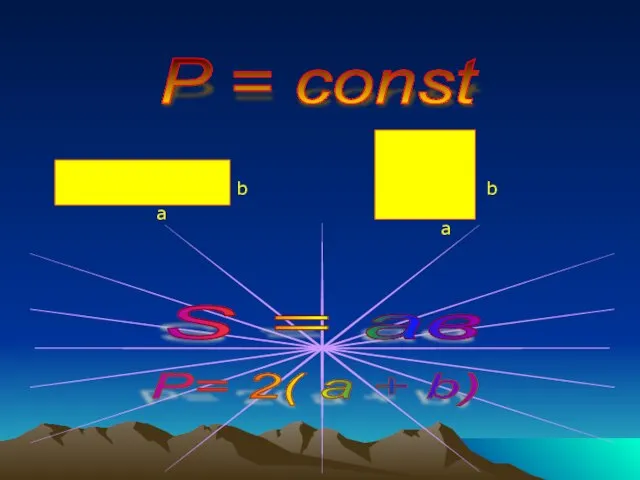
- 9. P = const a a b b S = ав Р= 2( a + b)
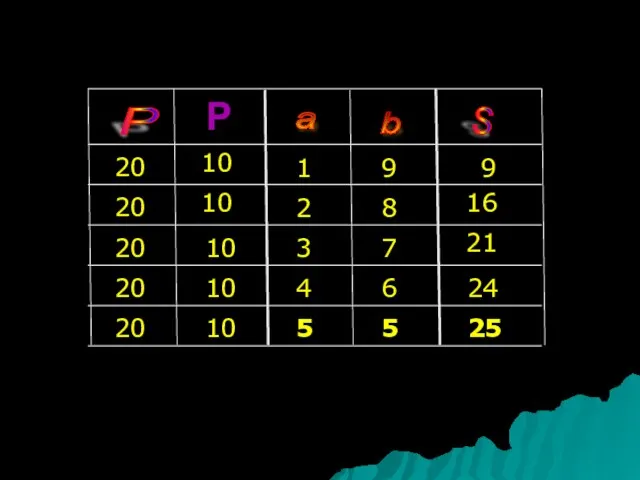
- 10. P a b S 20 20 20 20 20 10 10 10 3 9 2 1
- 11. Из всех прямоугольников, имеющих один и тот же периметр, наибольшую площадь имеет квадрат!
- 12. S пр пар кв P = const
- 14. Скачать презентацию




 Арккосинус. Решение уравнения cos t = a
Арккосинус. Решение уравнения cos t = a Повторение пройденного (1 класс)
Повторение пройденного (1 класс) Обратные тригонометрические функции
Обратные тригонометрические функции Օբյեկտ-կողմնորոշված ծրագրավորման լեզու
Օբյեկտ-կողմնորոշված ծրագրավորման լեզու Определенный интеграл. Формула Ньютона - Лейбница
Определенный интеграл. Формула Ньютона - Лейбница Уравнение окружности
Уравнение окружности 6cc84cfba09801fa77f2178065bede8f
6cc84cfba09801fa77f2178065bede8f Решение заданий олимпиады ПРОФИ 2017
Решение заданий олимпиады ПРОФИ 2017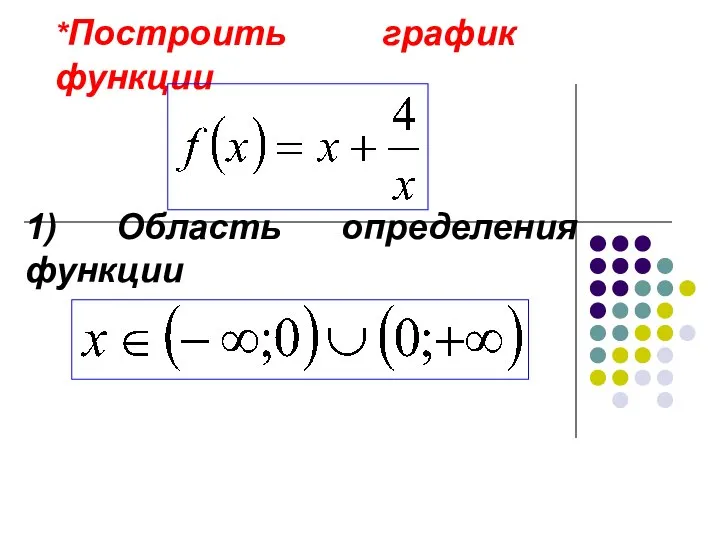 Построение графиков функций
Построение графиков функций Приемы вычислений для случаев вида 27+7
Приемы вычислений для случаев вида 27+7 Целостный подход. Производная функции y=f'(x)
Целостный подход. Производная функции y=f'(x)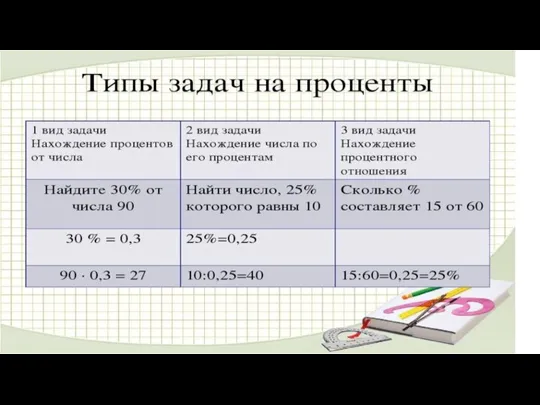 Задачи на проценты
Задачи на проценты теория вероятностей задачи
теория вероятностей задачи Кусочная функция
Кусочная функция Функция. Свойства функции. График функции
Функция. Свойства функции. График функции Уравнения, системы уравнений. Задание №9
Уравнения, системы уравнений. Задание №9 Ортогональная проекция плоской фигуры на плоскость и ее площадь
Ортогональная проекция плоской фигуры на плоскость и ее площадь Дифференциальные уравнения с разделяющимися переменными
Дифференциальные уравнения с разделяющимися переменными Компоненты вычитания
Компоненты вычитания Движение
Движение Презентация на тему Математика и спорт (5 класс)
Презентация на тему Математика и спорт (5 класс)  Сравнение целых чисел
Сравнение целых чисел Уроки математики в Школе смешариков
Уроки математики в Школе смешариков Правильные многогранники
Правильные многогранники Решето эратосфена
Решето эратосфена Юный математик
Юный математик Площади поверхностей и объёмы тел вращения
Площади поверхностей и объёмы тел вращения Роль математики в медицине
Роль математики в медицине