Слайд 2Определение
Показательные неравенства –
это неравенства, в которых неизвестное содержится в показателе

Слайд 3Простейшие показательные неравенства – это неравенства вида:
где a > 0, a ≠

1, b – любое число.
Слайд 4Решение простейших показательных неравенств
Знак неравенства
Сохраняется
Меняется
При решении простейших неравенств используют свойства возрастания

или убывания показательной функции.
Слайд 5Решения показательных неравенств:
Способ уравнивания показателей.
Разложения на множители.
Введения новой переменной.

Слайд 8Способ 2. Разложение на множители
3 > 1, ф-ция ↑
Ответ:

Слайд 9Способ 3. Введение новой переменной
Ответ: 0 < х < 2.
3>1, то

Слайд 10Решите неравенства
Ответ: х € D (f)
х € D

Слайд 11Решите неравенство
-5
5 >1 ф-ия ↑
-5

Слайд 12Решите неравенство
7>1 ф-ия ↑
х1 = 2 х2 = 3

Слайд 13Решите неравенство
32х – 4 ∙3х + 3 ≤ 0
3х = y
y² -

4y + 3 ≤ 0
у = 3; 1
1≤ y ≤ 3
1≤ 3x ≤ 3
30 ≤ 3x ≤ 3
3 > 1 ф-ция ↑
0 ≤ х ≤ 1
Х € [0;1]
Ответ: [0;1]
Резерв













 Основные распределения математической статистики
Основные распределения математической статистики Учимся писать цифры
Учимся писать цифры Презентация на тему Алгебраические уравнения произвольных степеней 10 класс
Презентация на тему Алгебраические уравнения произвольных степеней 10 класс  Прямая и обратная пропорциональные зависимости
Прямая и обратная пропорциональные зависимости Старинные меры длины и веса
Старинные меры длины и веса Финансовая математика: банки, вклады, кредиты. Часть 2
Финансовая математика: банки, вклады, кредиты. Часть 2 Неопределенный интеграл Ч2, свойства неопределенного интеграла
Неопределенный интеграл Ч2, свойства неопределенного интеграла Обратная матрица
Обратная матрица Трапеция. Свойство углов равнобедренной трапеции
Трапеция. Свойство углов равнобедренной трапеции Презентация на тему Касательная к графику функции
Презентация на тему Касательная к графику функции  Сложение и вычитание целых и дробных чисел
Сложение и вычитание целых и дробных чисел Измерение длины отрезка
Измерение длины отрезка Ребусы от тётушки Совы
Ребусы от тётушки Совы 21baz
21baz Приёмы умножения числа 2
Приёмы умножения числа 2 Тренажер вычисления производной
Тренажер вычисления производной Решение систем с неизвестными множествами
Решение систем с неизвестными множествами Nepreryvnost_funktsii (1)
Nepreryvnost_funktsii (1) Построения в пространстве
Построения в пространстве Нарушение осанки и плоскостопие
Нарушение осанки и плоскостопие Правильные многогранники
Правильные многогранники Орел. Решка. Формула вероятности
Орел. Решка. Формула вероятности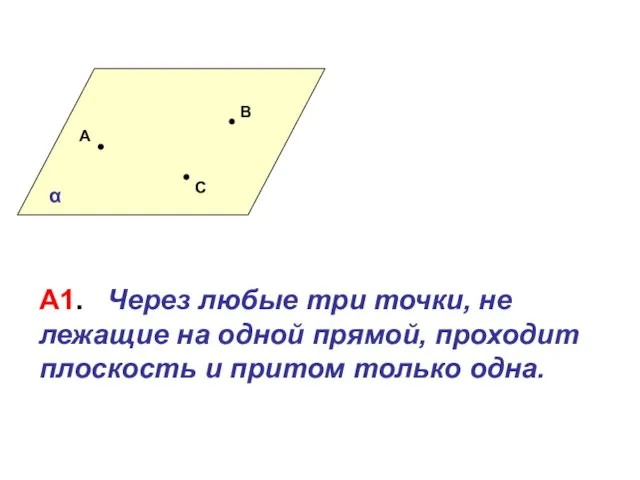 Плоскости
Плоскости Презентация на тему Сложение целых чисел
Презентация на тему Сложение целых чисел  Сложение и вычитание алгебраических дробей с разными знаменателями. 8 класс
Сложение и вычитание алгебраических дробей с разными знаменателями. 8 класс Презентация на тему РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ
Презентация на тему РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ  Проверочная работа. 5 класс
Проверочная работа. 5 класс Свойства числовых функций
Свойства числовых функций