Слайд 2В основе математического исследования лежит
Дедуктивный метод
Индуктивный метод
Слайд 3Дедуктивный метод
Дедуктивный метод – это рассуждение, исходным моментом которого является общее утверждение,
а заключительным – частный результат.
Слайд 4Индуктивный метод
Индуктивный метод – рассуждение, при котором, опираясь на ряд частных результатов
приходят к одному общему выводу.
Слайд 5Пример рассуждения по индукции
Требуется установить, что каждое четное число в пределах от

4 до 100 можно представить в виде суммы двух простых чисел. Для этого переберем все интересующие нас числа и выпишем соответствующие суммы:
Слайд 64=2+2; 6=3+3; 8=3+5; 10=5+5; ...;
92=3+89; 94=5+89; 96=7+89; 98=9+89;
100=3+97.
Эти 49 равенств (мы выписали

только 9 из них) показывают, что утверждение о том, что любое четное число от 4 до100 можно представить в виде суммы двух простых чисел, верно и было доказано путем перебора всех частных случаев.
Слайд 7Это был пример полной индукции, когда общее утверждение доказывается для конечного множества

элементов при рассмотрении каждого из этих элементов.
Но чаще общее утверждение относится не к конечному, а к бесконечному множеству. В таких случаях общее утверждение может быть угаданным, полученным неполной индукцией. Оно может оказаться верным или неверным.
Слайд 10Итак, неполная индукция не считается в математике методом строгого доказательства, т.к. может

привести к ошибке. Во многих случаях, когда доказательство найти трудно, обращаются к особому методу рассуждений, который называется методом математической индукции.
Слайд 14Составляющие метода математической индукции
Пусть нужно доказать справедливость А(n), где n – любое

натуральное число.
Для этого сначала проверим справедливость А(n) для n=1(базис математической индукции).
Затем докажем, что для любого натурального числа k справедливо следующее: если А(k) – справедливо, то А(k+1), тоже справедливо(индукционный шаг).
Делаем вывод, что А(n) справедливо для любого n.













 Методика проверки и оценки алгебраических заданий повышенного уровня сложности
Методика проверки и оценки алгебраических заданий повышенного уровня сложности Признак перпендикулярности плоскостей
Признак перпендикулярности плоскостей Применение производной к исследованию функций и построению графиков
Применение производной к исследованию функций и построению графиков Вырезаем квадрат
Вырезаем квадрат Расстояния. Подготовка к ЕГЭ по математике 2019
Расстояния. Подготовка к ЕГЭ по математике 2019 Значение переменных верного равенства. Корни уравнений
Значение переменных верного равенства. Корни уравнений Осевая и центральная симметрия
Осевая и центральная симметрия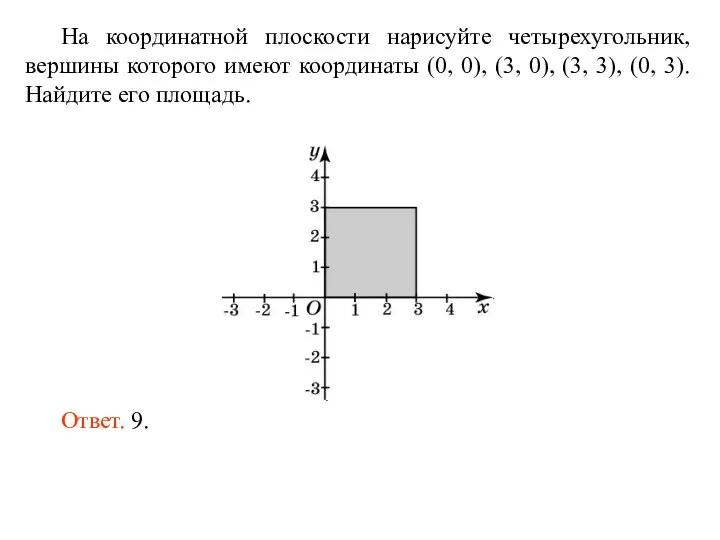 Площадь фигур
Площадь фигур Чтение и запись многозначных чисел. Класс миллионов. Класс миллиардов
Чтение и запись многозначных чисел. Класс миллионов. Класс миллиардов Марафон. Вопросы
Марафон. Вопросы Тела вращения. Конус
Тела вращения. Конус Медианы, биссектрисы и высота треугольника
Медианы, биссектрисы и высота треугольника Математика для детей (тест)
Математика для детей (тест) 3 класс. Разминка
3 класс. Разминка I признак подобия треугольников
I признак подобия треугольников Математика. 1 класс
Математика. 1 класс Lektsia-2-russ
Lektsia-2-russ Методика решения качественных и количественных задач
Методика решения качественных и количественных задач Стереометрия. Аксиомы стереометрии
Стереометрия. Аксиомы стереометрии Построение сечений. Задачи
Построение сечений. Задачи Структура ОГЭ 2020 по математика
Структура ОГЭ 2020 по математика Логика и математическая логика. История логики. Алгебра высказываний
Логика и математическая логика. История логики. Алгебра высказываний Четырехугольники. Параллелограмм
Четырехугольники. Параллелограмм Число и цифра (старшая группа)
Число и цифра (старшая группа) Наука статистика
Наука статистика История возникновения числа ПИ
История возникновения числа ПИ Модуль. Определение. Свойства. Геометрический смысл модуля
Модуль. Определение. Свойства. Геометрический смысл модуля Презентация на тему Приведение дробей к общему знаменателю (6 класс)
Презентация на тему Приведение дробей к общему знаменателю (6 класс)