Методика проверки и оценки алгебраических заданий повышенного уровня сложности

Должны быть решения квадратных уравнений, а не просто записанные корни.
Вывод «нет корней» должен сопровождаться вычислением отрицательного дискриминанта (выделением полного квадрата), кроме случая использования знака равносильности и совокупности. При равносильности ответ записывается в виде множества (за другой вид не снижать).
Если используют обратную теорему Виета, то она должна быть прописана.
Не снижать за то, что корни выписаны не в порядке возрастания.
Если ввели подстановку и прописали ограничение на переменную неправильно – ошибка.

Знак равносильности между разными переменными писать нельзя (разные множества).
Ввели новую переменную, но не описали ее ограничение. Лишний корень при этом отбросили, сославшись на непрописанное ограничение, да еще может быть ответ не упрощен (сокращение) – 1 балл.
Если в ответе корни не сокращены, но в процессе решения вся логика присутствует - 2 балла.
Правильное логическое решение, корни верные, но при этом написана какая-нибудь глупость про переменные – это проблема с обоснованностью – 1 балл.

2 балла

0 баллов

Обращать внимание на единицы измерения переменных! Если их нет (т.е. нет вообще нигде в процессе решения, а не частично – у одной из трех переменных), но ответ верный - 1 балл.
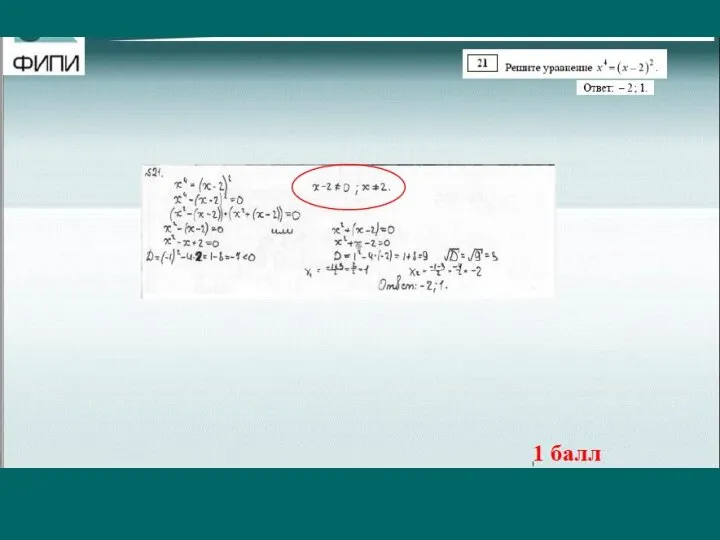
При работе с дробно-рациональным уравнением должно быть прописано, что знаменатель не равен нулю! – если нет, то 1 балл при верном ответе.
Уравнение составлено неправильно – 0 баллов.
Отбор корней должен быть обоснованный.
Если дробно-рациональное уравнение получено из системы, то снижать балл из-за не прописанного ОДЗ не надо.

Логические ошибки (0 баллов):
Перенос слагаемого из одной части уравнения в другую и при этом знак не изменили.
При расчете корней квадратного уравнения внесено неправильное значение коэффициента:

При расчете корней квадратного уравнения неправильно сокращена дробь:

Вычислительные ошибки(1 балл):
Отсутствуют промежуточные расчеты, а в итоговом числе после упрощения не то значение:

Все признаки и свойства должны быть четко прописаны.
«Если две прямые пересекаются третьей и есть два равных угла, то прямые параллельны» - данное утверждение ошибочно.
Четко прописаны названия углов, указаны параллельные прямые и секущая.
Если есть описание равных углов в решении, но нет на чертеже – баллы не снижать.
Накрестлежащие и внутренние накрестлежащие – эти оба термина правильные.

Утверждение о том, что «биссектриса параллелограмма отсекает от него равнобедренный треугольник», не прописано отдельным свойством в учебниках, которые используются в массовом обучении. Оно есть в Мерзляке (менее 8%), но он не массовый, поэтому такие утверждения должны быть доказаны или очень четко сформулированы. Фразы вида: «Т.к. это биссектриса в параллелограмме, то треугольник равнобедренный» - это необоснованное решение.
Если не указаны параллельные прямые и секущая – минус 1 балл за необоснованность.

Не придираться к словам: признак, свойство (дети их часто путают), если формулировка прописана верно.
Если используем математический знак подобия между треугольниками, то обращаем внимание на последовательность букв и снижаем балл. Если в свободном тексте указывают два треугольника, то буквы могут иметь любую последовательность

Нет логических ошибок, нет вычислительных ошибок, но забыли упомянуть об использовании теоремы Пифагора – не снижать.
По свойству касательной – запись допустима и балл не снижать.

В задании снижен 1 балл за 3 пункт – в скобках не объяснение, а комментарий.

0 баллов

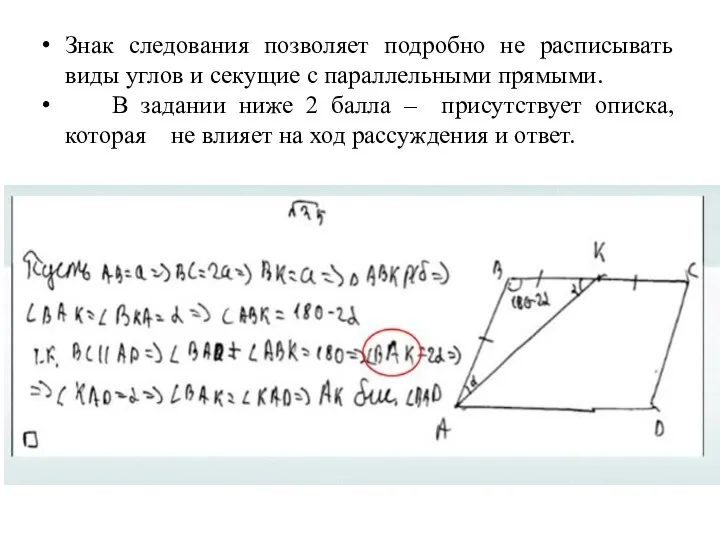
Знак следования позволяет подробно не расписывать виды углов и секущие с параллельными прямыми.
В задании ниже 2 балла – присутствует описка, которая не влияет на ход рассуждения и ответ.

Прописано равенство сторон треугольника и без дополнительных пояснений равенство углов, не снижаем – 2 балла.

1 балл – неправильная формулировка признака в скобках, а именно угол между пропорциональными сторонами. Об угле между сторонами нигде в задаче не указано.

Логические ошибки – 0 баллов:
При сложении двух отрезков вместо радиуса используют значение диаметра.
Работая с теоремой Пифагора забыли квадрат:

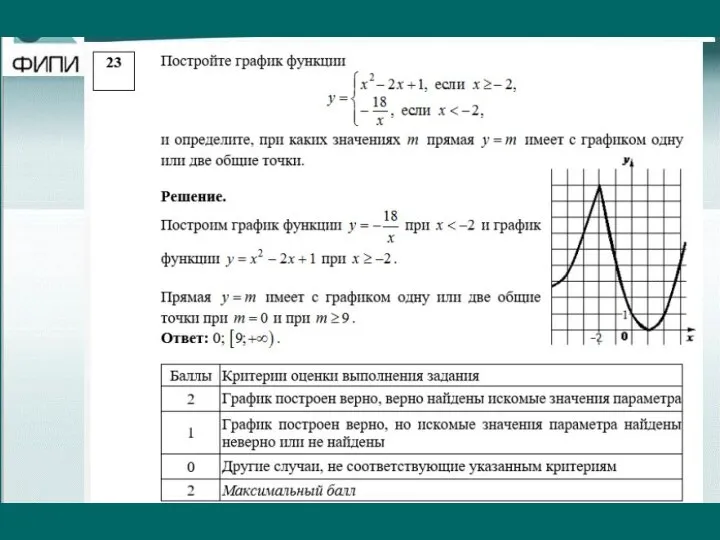
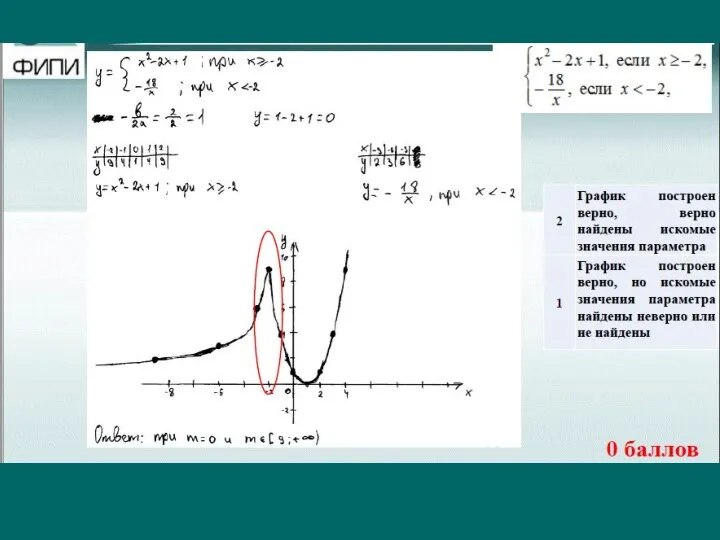
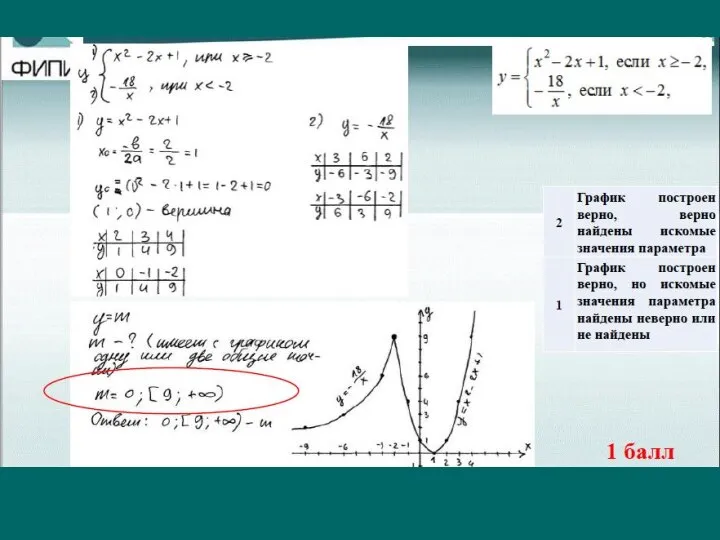
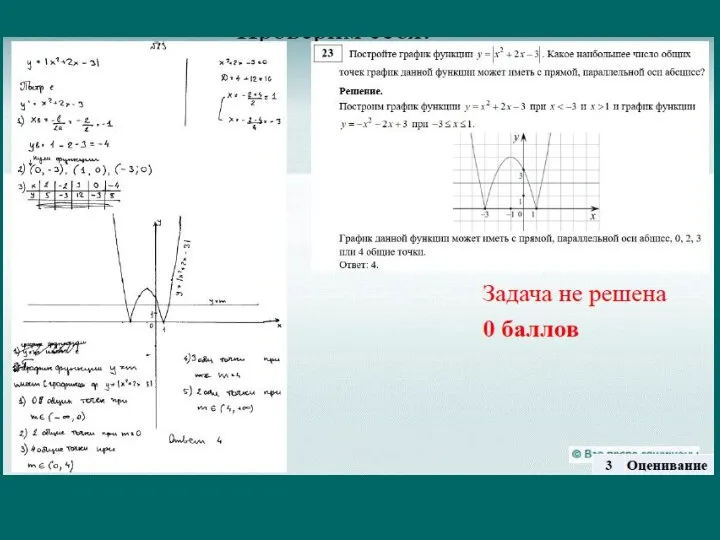
Если функция задана кусочно, то граничная точка должна быть подставлена и прописана в таблице у обоих функций. Иначе 0б.
Точки, по которым идет построение, должны быть видны на графике.
Должно быть (желательно) подробное описание построения графика: название (гипербола, парабола), найдены координаты вершины, указаны направление ветвей.
При отборе параметра, на графике должно быть изображено несколько горизонтальных линий, прописаны все случаи параметра. Параметр – это исследование, а не устный ответ.

В подобии треугольников неверно составлено соотношение.

0 баллов – ошибочное утверждение, что D середина CB.