Построение сечений

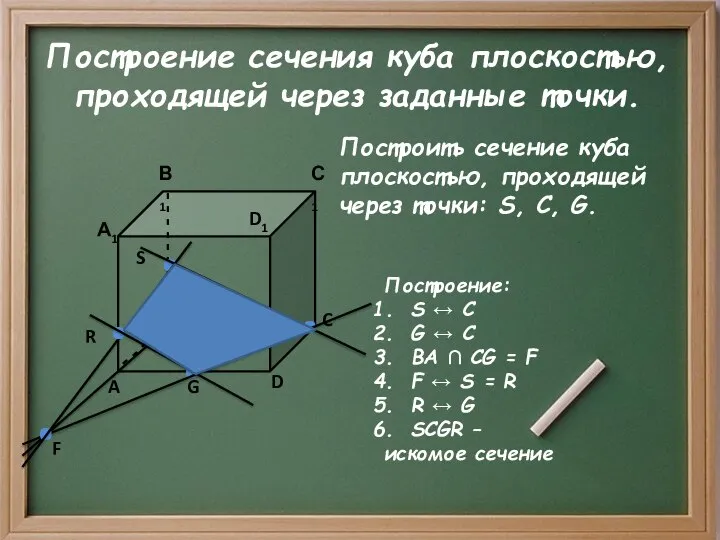
Построение сечения куба плоскостью, проходящей через заданные точки.
- - - - - - - - - - -
- - - - - - - - - - -
- - - - -
А1
В1
С1
D1
A
B
D
C
.
.
.
Построение:
S ↔ C
G ↔ C
BA ∩ CG = F
F ↔ S = R
R ↔ G
SCGR –
искомое сечение
S
G
.
F
R
.
Построить сечение куба плоскостью, проходящей через точки: S, С, G.

Построение сечения тетраэдра плоскостью, проходящей через заданные точки.
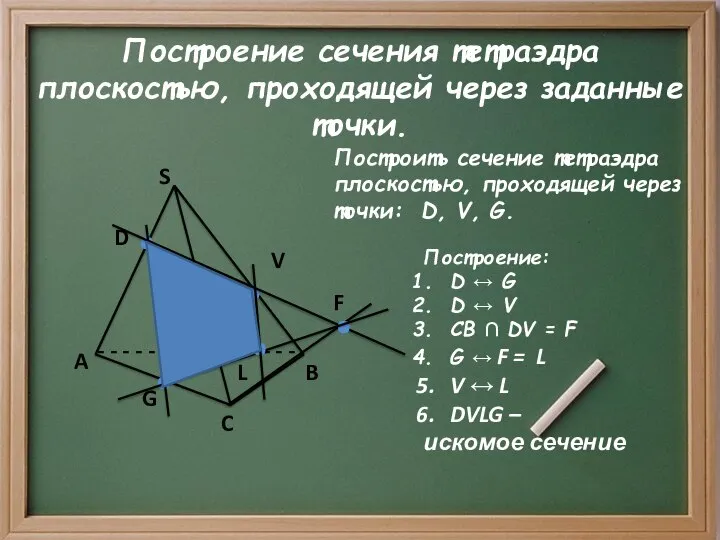
Построить сечение тетраэдра плоскостью, проходящей через точки: D, V, G.
- - - - - - - - - - - - - - - -
S
A
B
C
.
.
.
G
V
D
Построение:
D ↔ G
D ↔ V
CB ∩ DV = F
G ↔ F = L
V ↔ L
DVLG –
искомое сечение
.
F
.
L