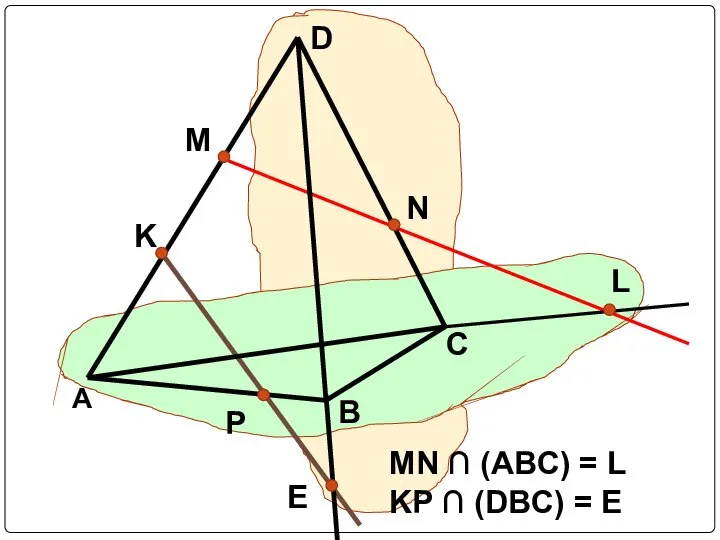
Слайд 2MN ∩ (ABC) = L
KP ∩ (DBC) = E
Слайд 3M
N
K
Прямая KX – след секущей плоскости
на плоскости основания.
Прямая KD – след секущей
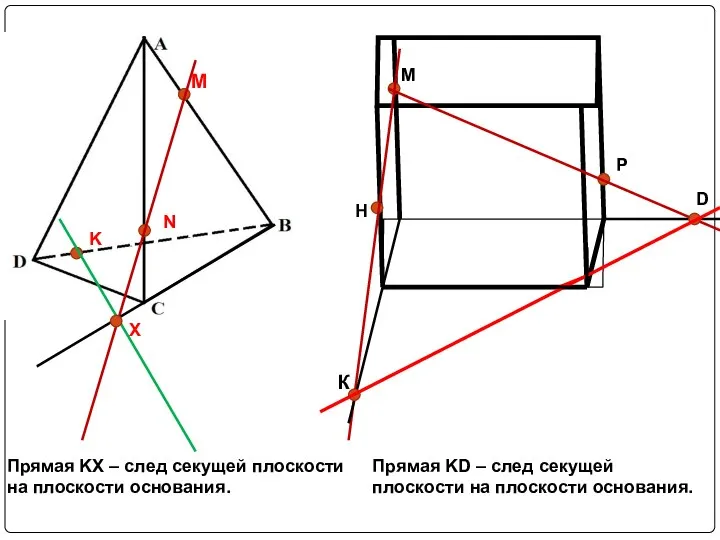
плоскости на плоскости основания.
Слайд 4Секущей плоскостью многогранника называется любая плоскость, по обе стороны от которой имеются
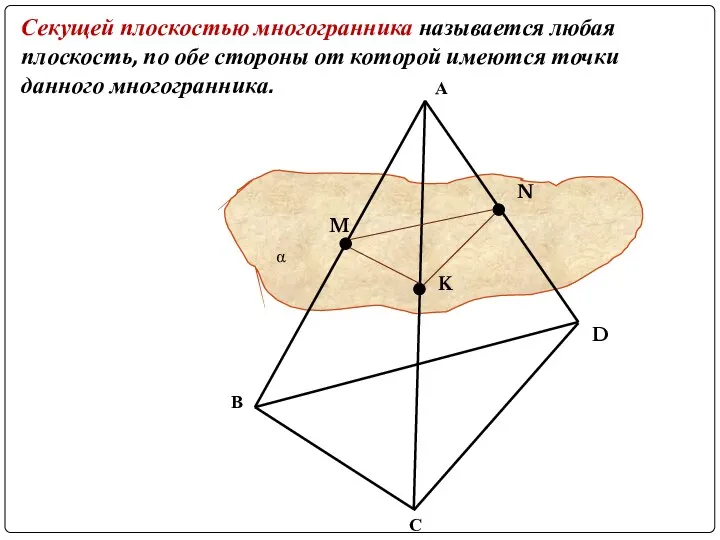
точки данного многогранника.
Слайд 5Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти
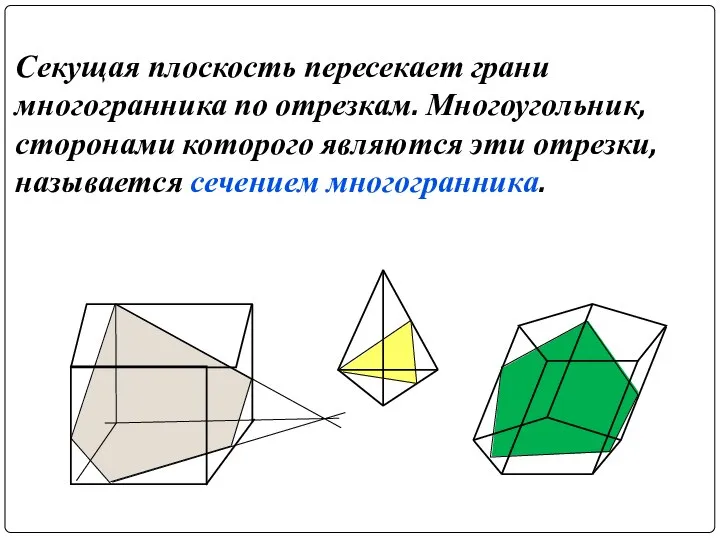
отрезки, называется сечением многогранника.
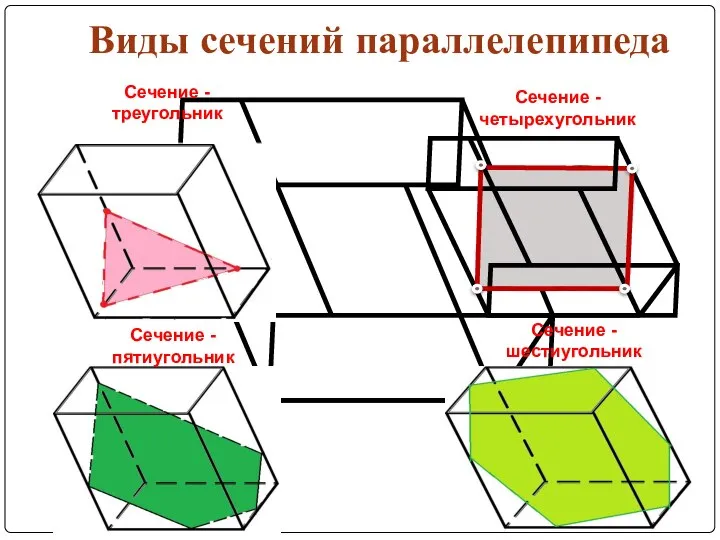
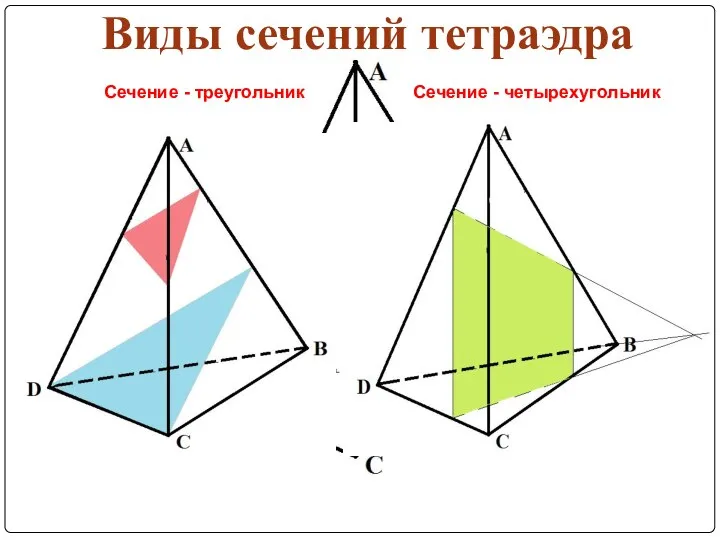
Слайд 7Виды сечений параллелепипеда
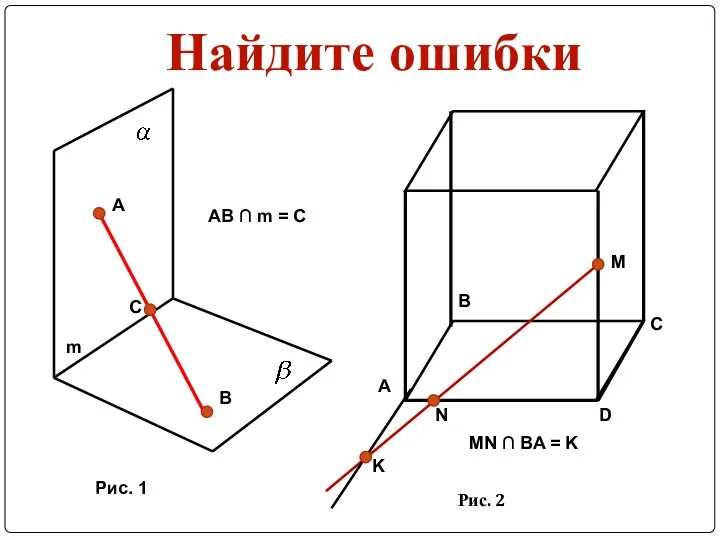
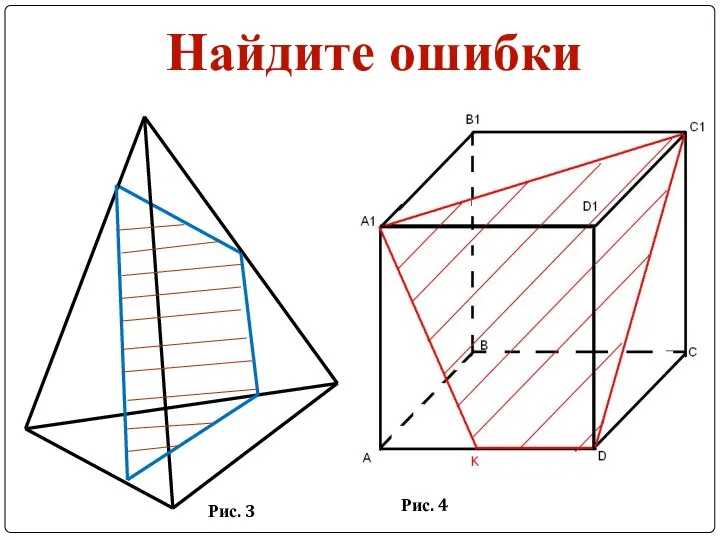
Слайд 8Найдите ошибки
A
B
C
m
AB ∩ m = C
Рис. 1
A
B
C
D
M
N
K
MN ∩ BA = K
Рис. 2
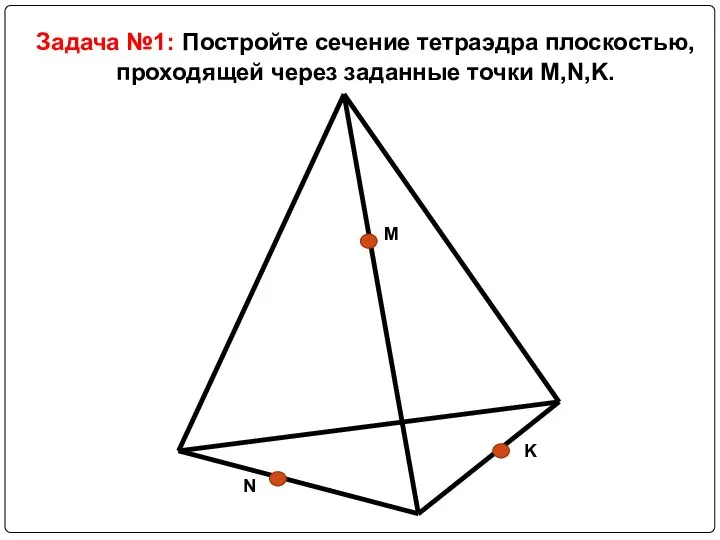
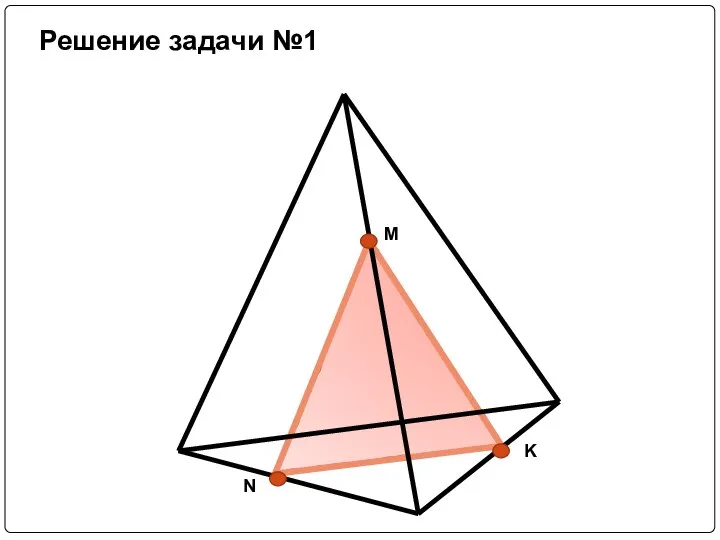
Слайд 10Задача №1: Постройте сечение тетраэдра плоскостью, проходящей через заданные точки M,N,K.
Слайд 12Задача №2. Дан тетраэдр DABC. Постройте сечение тетраэдра плоскостью MNK, если M,
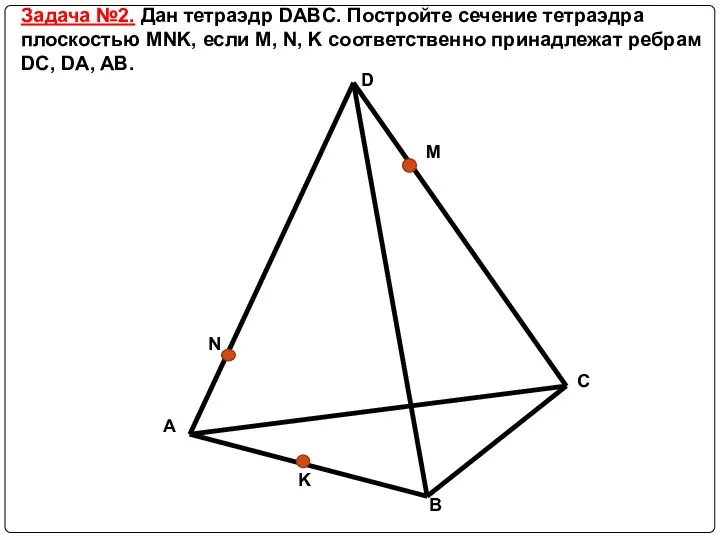
N, K соответственно принадлежат ребрам DC, DA, AB.
Слайд 13Решение задачи №2
1. MN ∩ AC = X
2. XK ∩ BC =
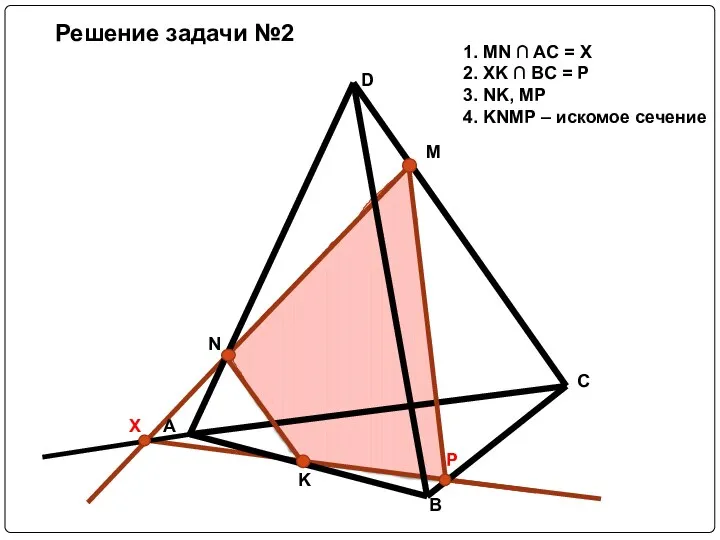
P
3. NK, MP
4. KNMP – искомое сечение
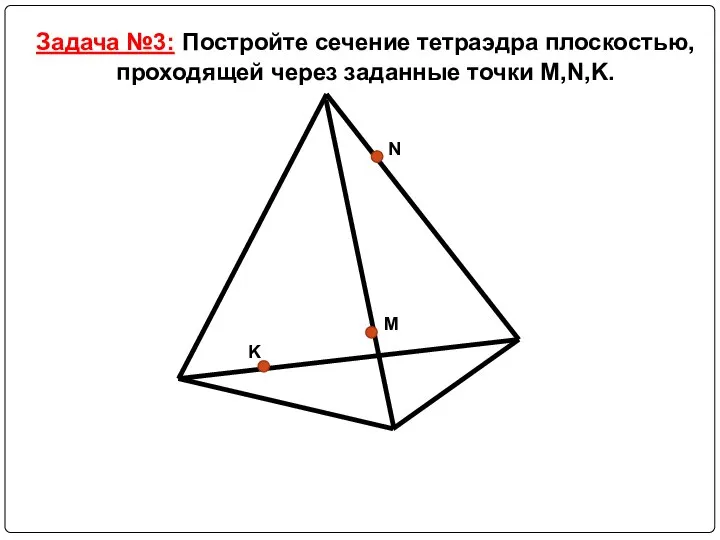
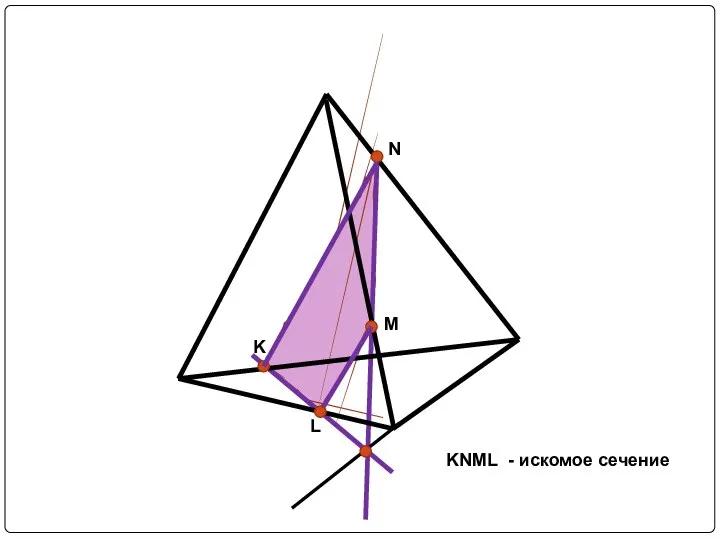
Слайд 14Задача №3: Постройте сечение тетраэдра плоскостью, проходящей через заданные точки M,N,K.
Слайд 16Задача № 4 Постройте сечение тетраэдра DABC плоскостью MNK, если M и
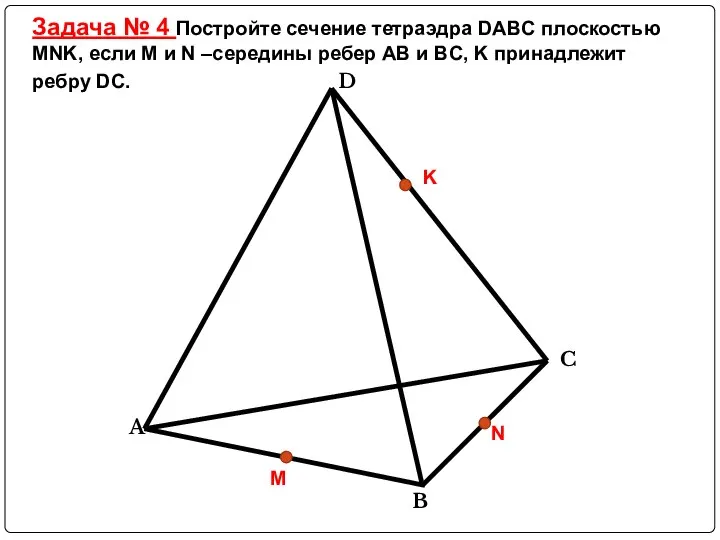
N –середины ребер AB и BC, K принадлежит ребру DC.
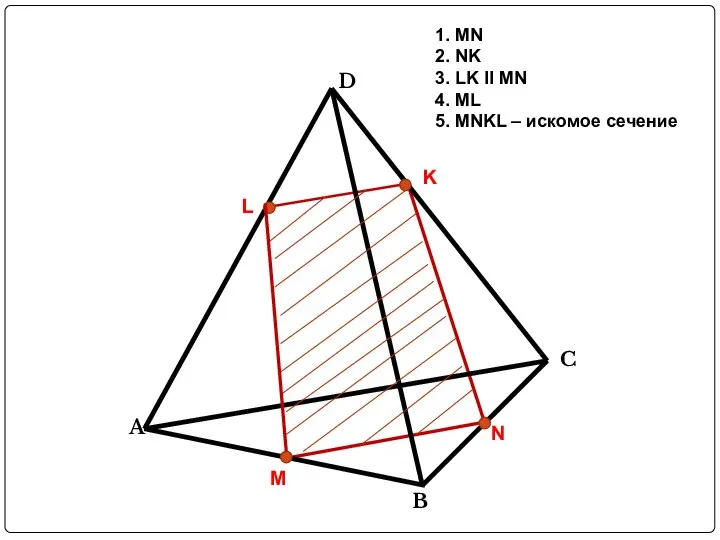
Слайд 17L
1. MN
2. NK
3. LK II MN
4. ML
5. MNKL – искомое сечение
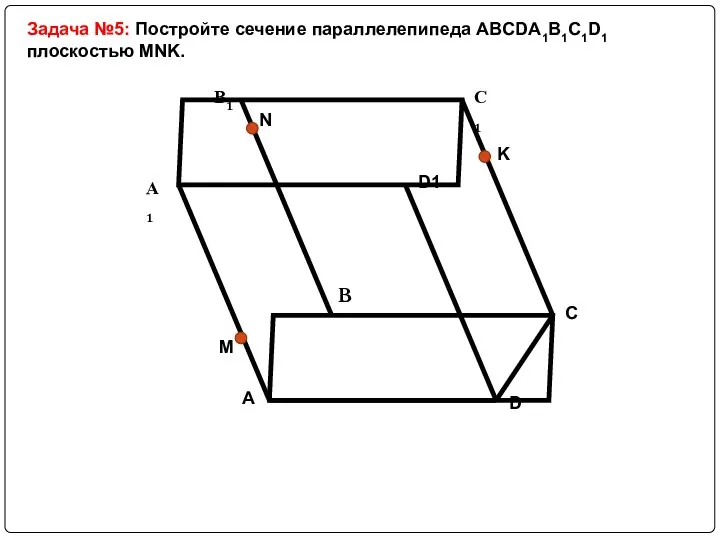
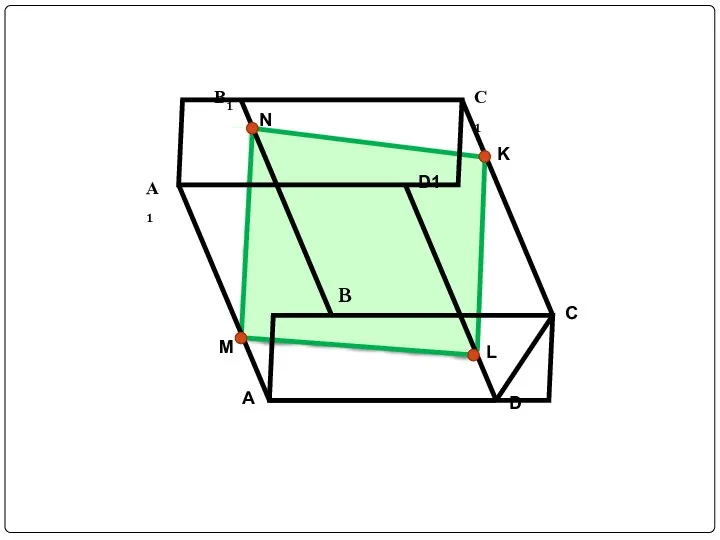
Слайд 18Задача №5: Постройте сечение параллелепипеда ABCDA1B1C1D1 плоскостью MNK.
Слайд 20Задача №6
Постройте сечение параллелепипеда ABCDA1B1C1D1 плоскостью PTO, если P, T,O принадлежат соответственно
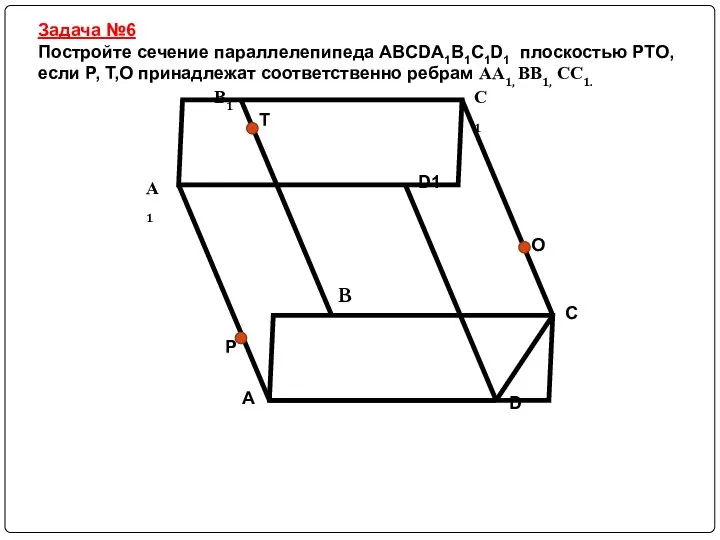
ребрам АА1, ВВ1, СС1.
Слайд 21TO ∩ BC = M
TP ∩ AB = N
NM ∩ AD =
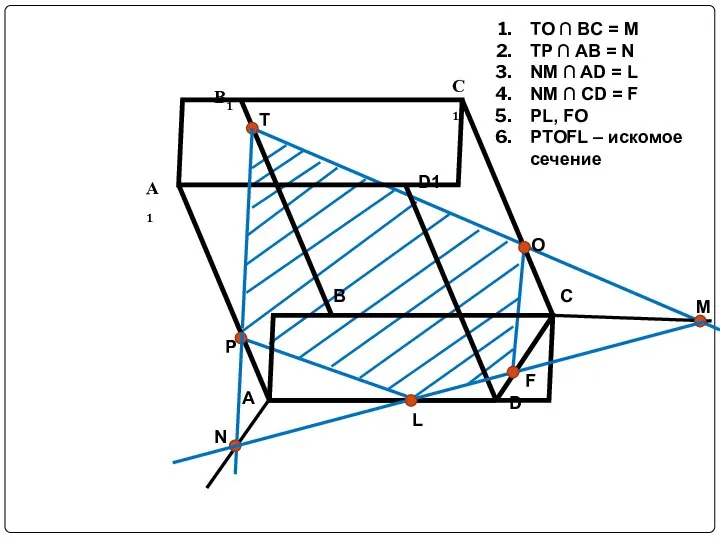
L
NM ∩ CD = F
PL, FO
PTOFL – искомое сечение
Слайд 22Задача №7: Постройте сечение параллелепипеда плоскостью KMN.
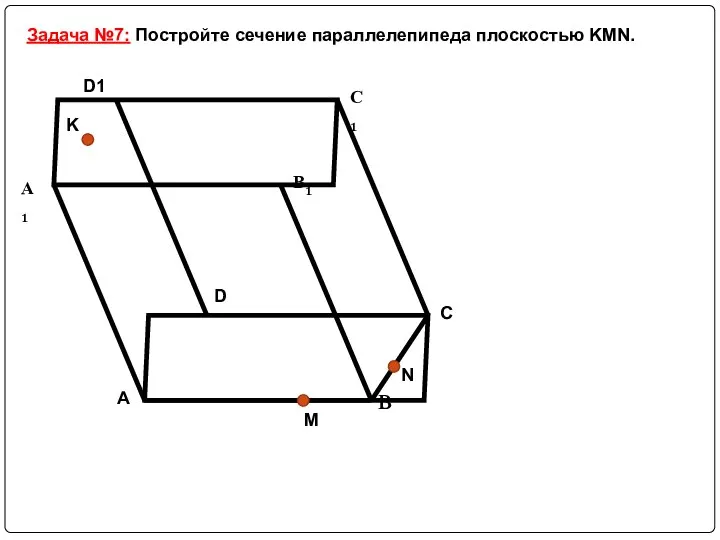
Слайд 23MN ∩ DA = Q
QK ∩ AA1 = P
PM
KF II MN
FE II
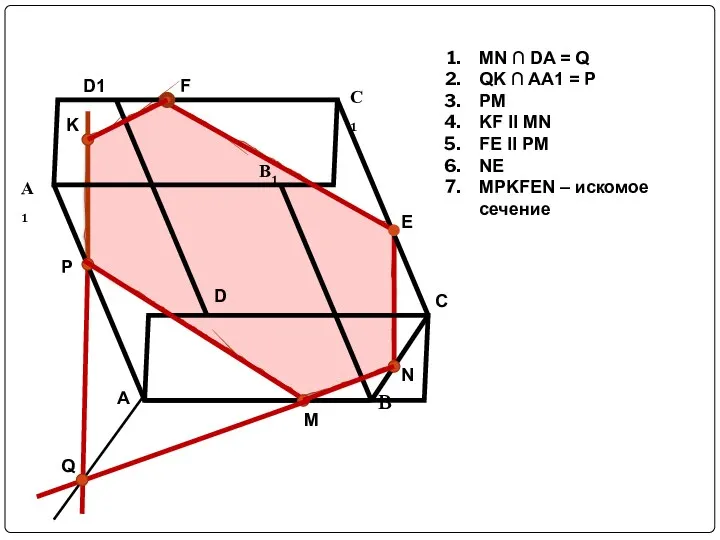
PM
NE
MPKFEN – искомое сечение
Слайд 24Итог урока:
«Мне понравился (не понравился) урок, потому что…»
«Сегодня на уроке я научился….»
«Мне

хочется, чтобы….»
«В этот урок я добавил(а) бы …»


















 Стохастические процессы
Стохастические процессы Презентация на тему Графическое решение уравнений
Презентация на тему Графическое решение уравнений  Старинные меры массы и длины
Старинные меры массы и длины Комплексные числа. Все формы
Комплексные числа. Все формы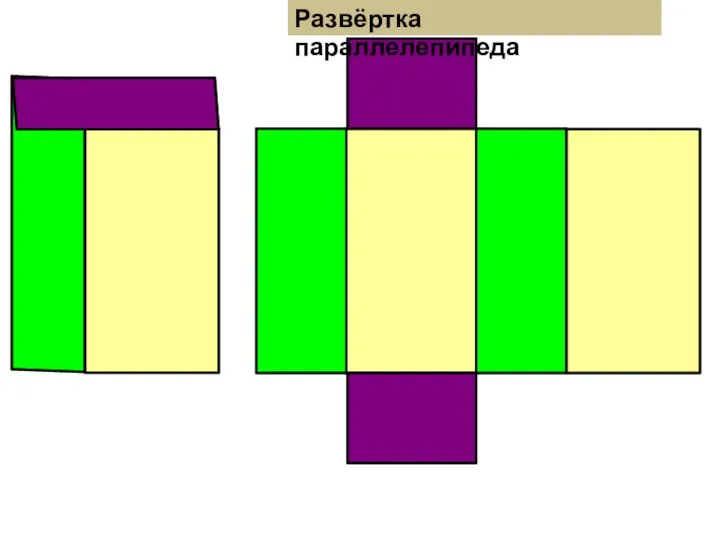 Развёртка параллелепипеда, куба, треугольной и четырёхугольной пирамиды. 5 класс
Развёртка параллелепипеда, куба, треугольной и четырёхугольной пирамиды. 5 класс Тригонометрические уравнения
Тригонометрические уравнения Квадратичная функция и её график. Методические материалы урока
Квадратичная функция и её график. Методические материалы урока Презентация на тему Объём многогранника
Презентация на тему Объём многогранника  Сближение меридианов. Международное геомагнитное аналитическое поле IGRF
Сближение меридианов. Международное геомагнитное аналитическое поле IGRF Задачи про форматы листов. Решение практико-ориентированных задач
Задачи про форматы листов. Решение практико-ориентированных задач Метод обратной матрицы решения систем линейных уравнений
Метод обратной матрицы решения систем линейных уравнений Методика работы с задачей на круговое движение
Методика работы с задачей на круговое движение Основные формулы тригонометрии
Основные формулы тригонометрии Деление обыкновенных дробей
Деление обыкновенных дробей 7490_md_sin_cos_tg_0
7490_md_sin_cos_tg_0 Пирамида и её элементы. Правильная пирамида
Пирамида и её элементы. Правильная пирамида Математика вокруг нас
Математика вокруг нас Время. Единицы времени
Время. Единицы времени Первый замечательный предел
Первый замечательный предел Математика ЕГЭ. Углы и прямые
Математика ЕГЭ. Углы и прямые Линейная функция и её график
Линейная функция и её график Теория вероятностей в задачах ЕГЭ
Теория вероятностей в задачах ЕГЭ Основы логистики
Основы логистики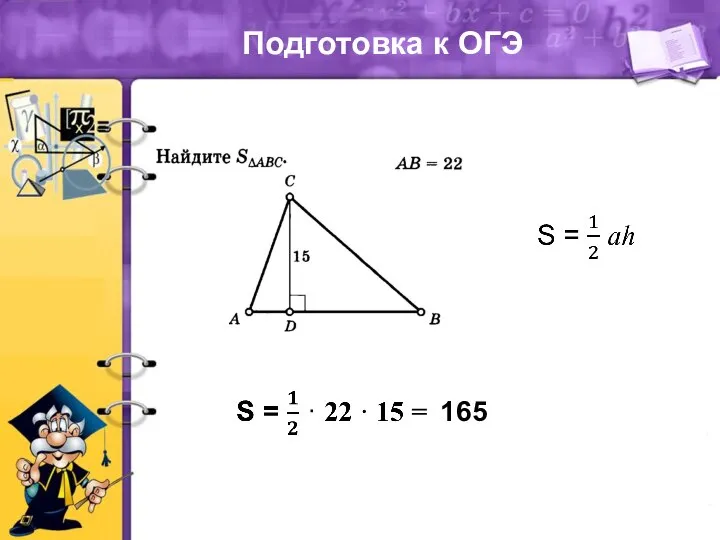 Теорема площади треугольника. Подготовка к ОГЭ
Теорема площади треугольника. Подготовка к ОГЭ Прямоугольник. Геометрия 8 класс
Прямоугольник. Геометрия 8 класс Логарифмические выражения
Логарифмические выражения Презентация по математике "Применение приёмов интерактивного обучения на уроках математики" -
Презентация по математике "Применение приёмов интерактивного обучения на уроках математики" -  Презентация на тему Метод координат в пространстве
Презентация на тему Метод координат в пространстве