Содержание
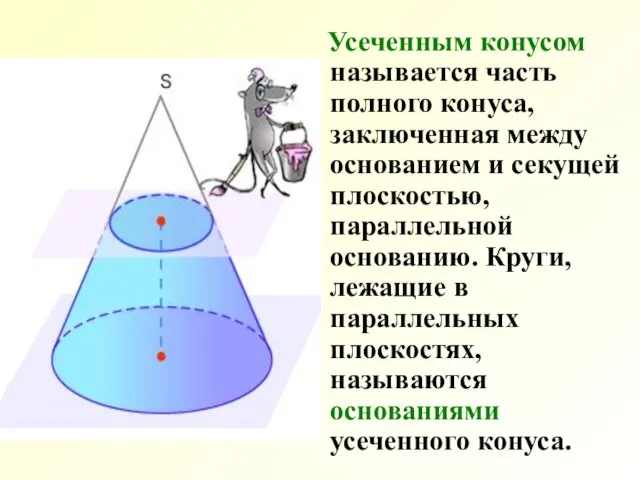
- 2. Усеченным конусом называется часть полного конуса, заключенная между основанием и секущей плоскостью, параллельной основанию. Круги, лежащие
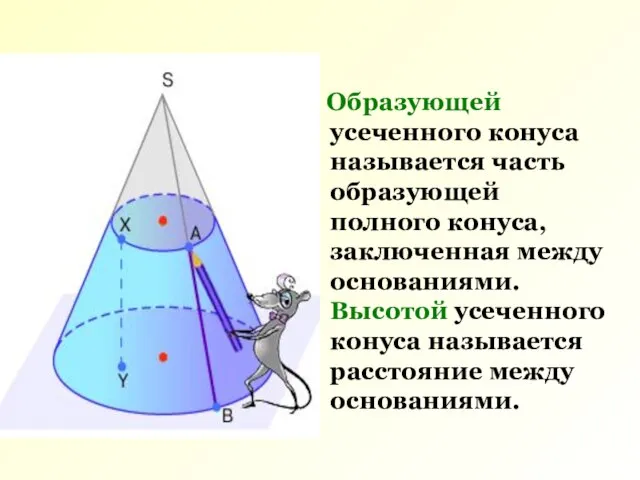
- 3. Образующей усеченного конуса называется часть образующей полного конуса, заключенная между основаниями. Высотой усеченного конуса называется расстояние
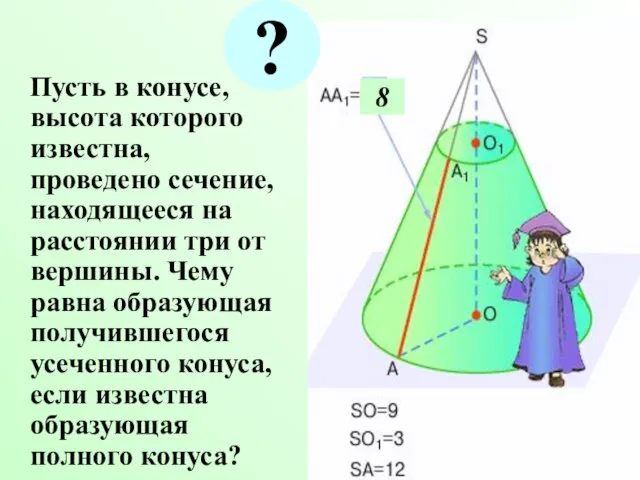
- 4. Пусть в конусе, высота которого известна, проведено сечение, находящееся на расстоянии три от вершины. Чему равна
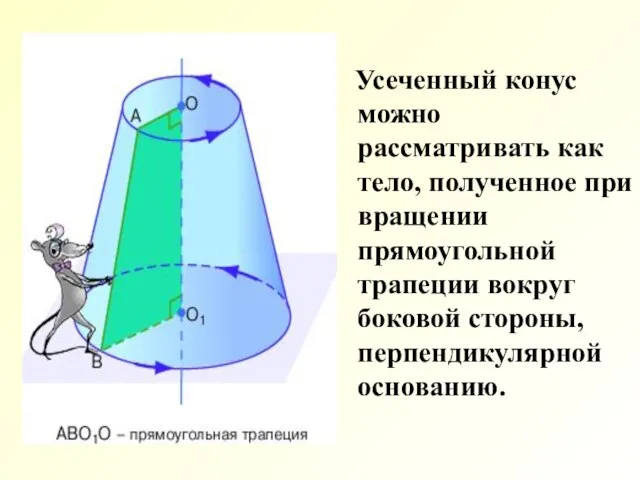
- 5. Усеченный конус можно рассматривать как тело, полученное при вращении прямоугольной трапеции вокруг боковой стороны, перпендикулярной основанию.
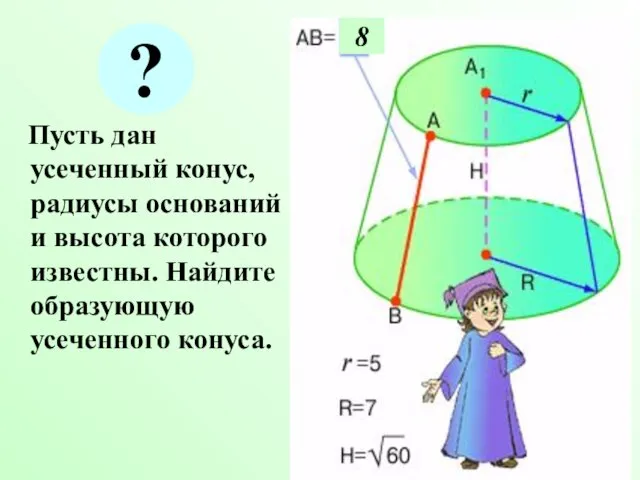
- 6. Пусть дан усеченный конус, радиусы оснований и высота которого известны. Найдите образующую усеченного конуса. 8 ?
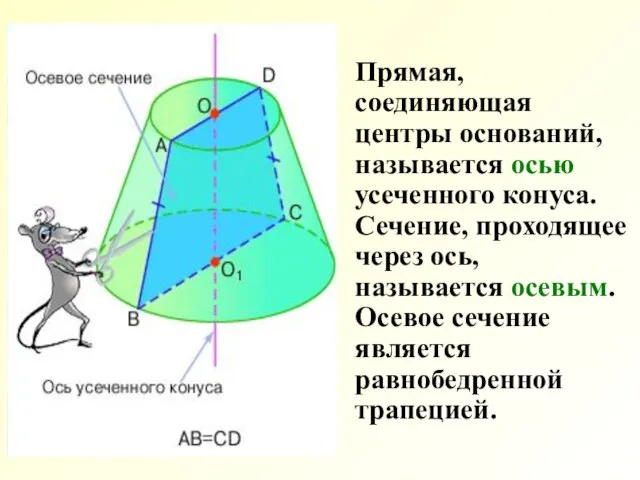
- 7. Прямая, соединяющая центры оснований, называется осью усеченного конуса. Сечение, проходящее через ось, называется осевым. Осевое сечение
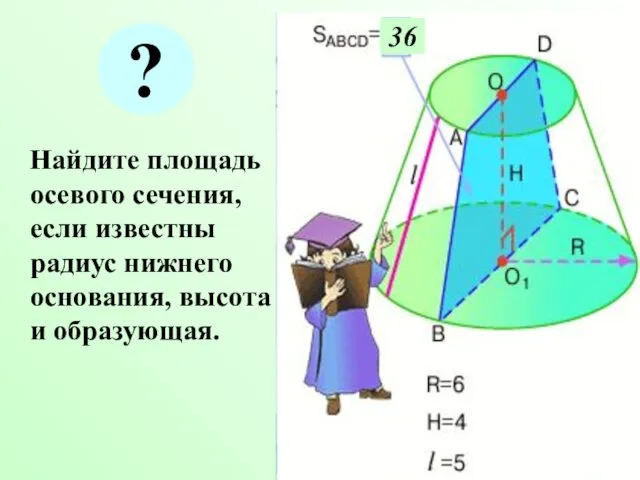
- 8. Найдите площадь осевого сечения, если известны радиус нижнего основания, высота и образующая. 36 ?
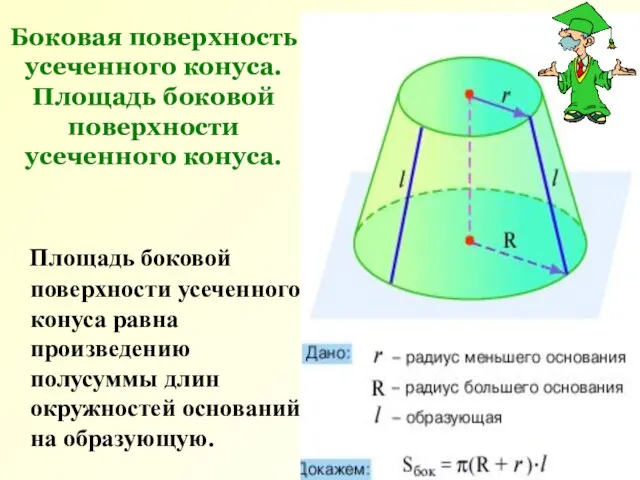
- 9. Боковая поверхность усеченного конуса. Площадь боковой поверхности усеченного конуса. Площадь боковой поверхности усеченного конуса равна произведению
- 10. Доказательство: Боковую поверхность усеченного конуса будем понимать как предел, к которому стремится боковая поверхность вписанной в
- 11. Доказательство: Впишем в конус правильную пирамиду. Ее боковая поверхность состоит из трапеций.
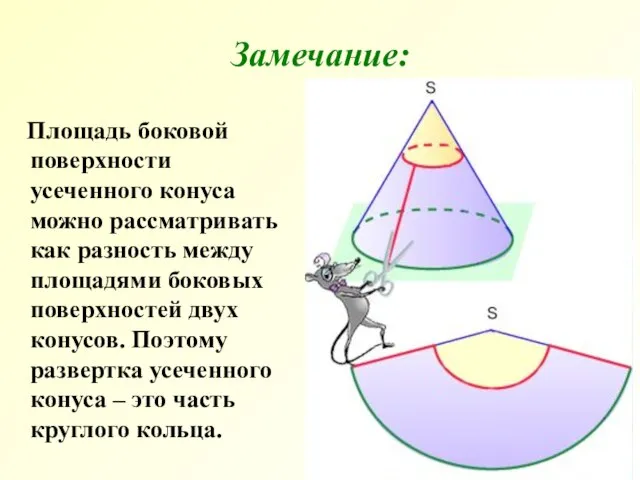
- 12. Площадь боковой поверхности усеченного конуса можно рассматривать как разность между площадями боковых поверхностей двух конусов. Поэтому
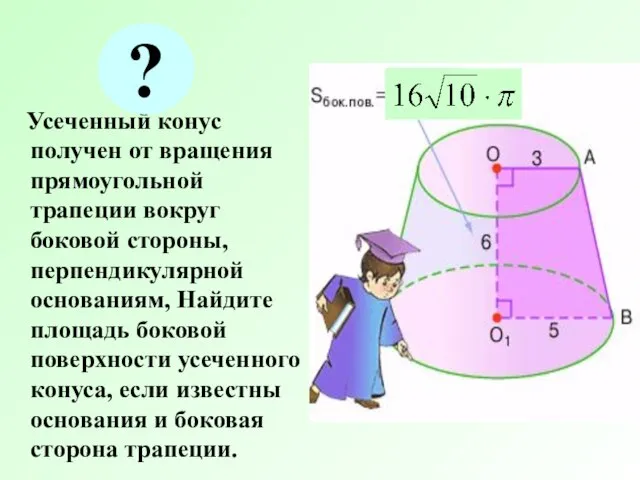
- 13. Усеченный конус получен от вращения прямоугольной трапеции вокруг боковой стороны, перпендикулярной основаниям, Найдите площадь боковой поверхности
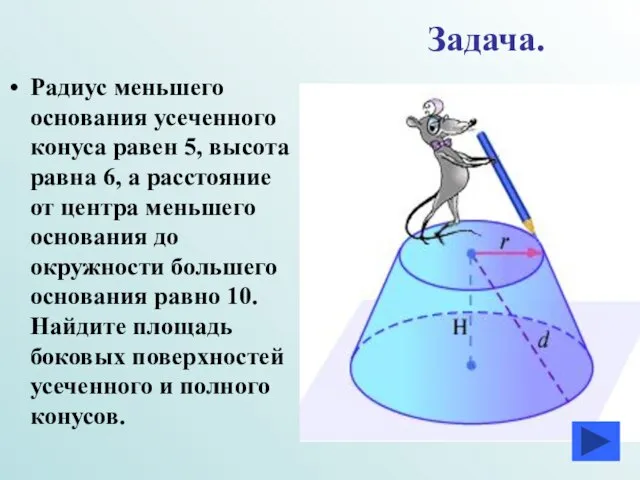
- 14. Задача. Радиус меньшего основания усеченного конуса равен 5, высота равна 6, а расстояние от центра меньшего
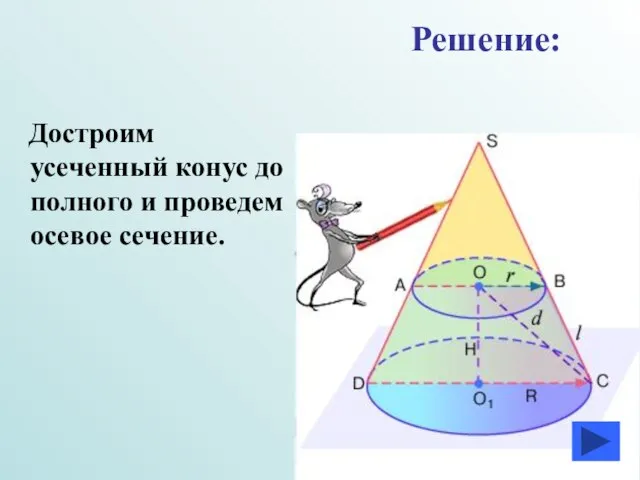
- 15. Достроим усеченный конус до полного и проведем осевое сечение. Решение:
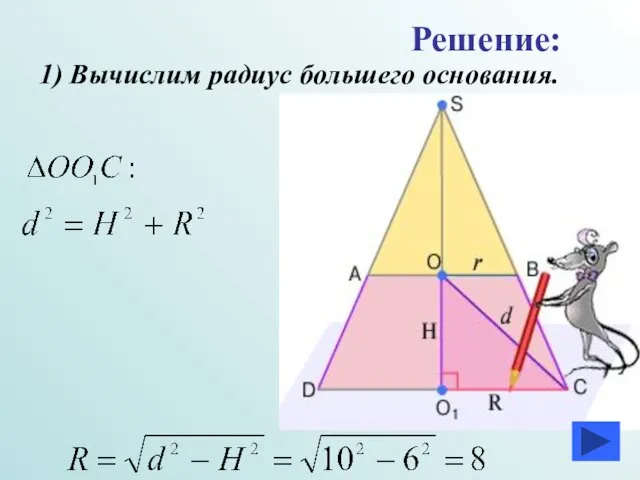
- 16. 1) Вычислим радиус большего основания. Решение:
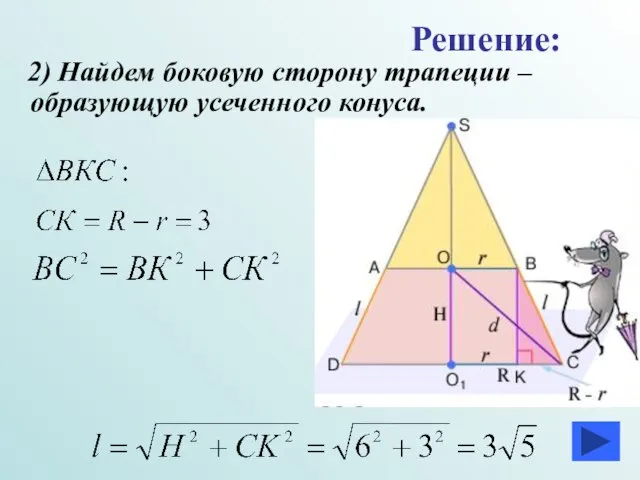
- 17. 2) Найдем боковую сторону трапеции –образующую усеченного конуса. Решение:
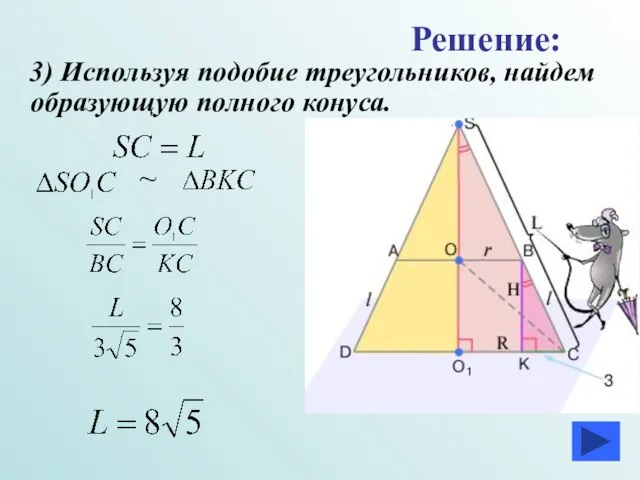
- 18. 3) Используя подобие треугольников, найдем образующую полного конуса. Решение: ~
- 19. 4) Подставим найденные значения в формулы для площадей боковой поверхности полного и усеченного конусов. Решение:
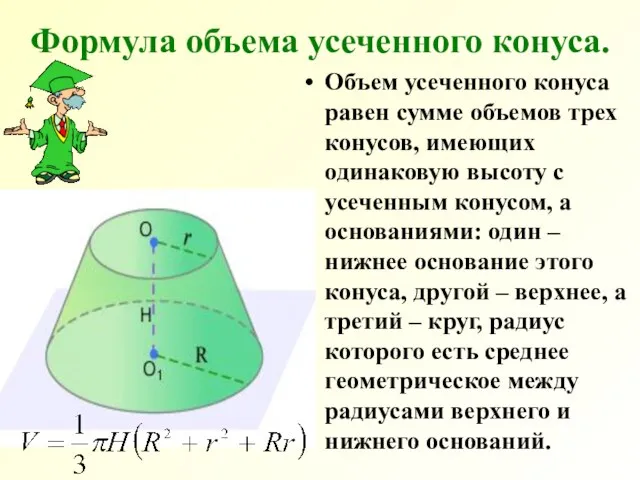
- 20. Формула объема усеченного конуса. Объем усеченного конуса равен сумме объемов трех конусов, имеющих одинаковую высоту с
- 21. Поместим на верхнем основании усеченного конуса малый конус, дополняющий его до полного и рассмотрим объем его
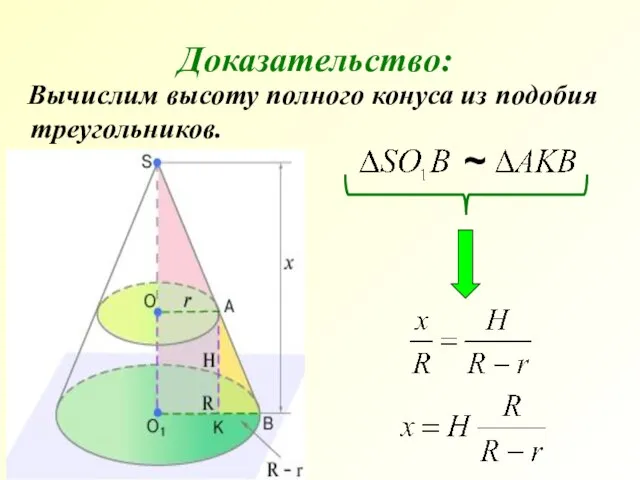
- 22. Вычислим высоту полного конуса из подобия треугольников. Доказательство: ~
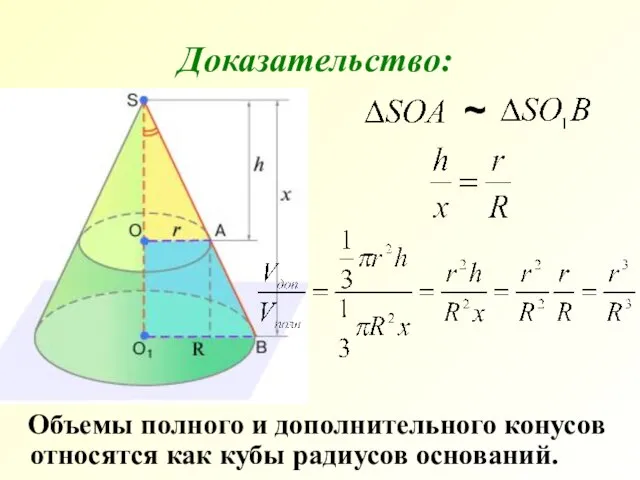
- 23. Объемы полного и дополнительного конусов относятся как кубы радиусов оснований. Доказательство: ~
- 24. Вычтем из объема большого конуса объем малого конуса. Доказательство:
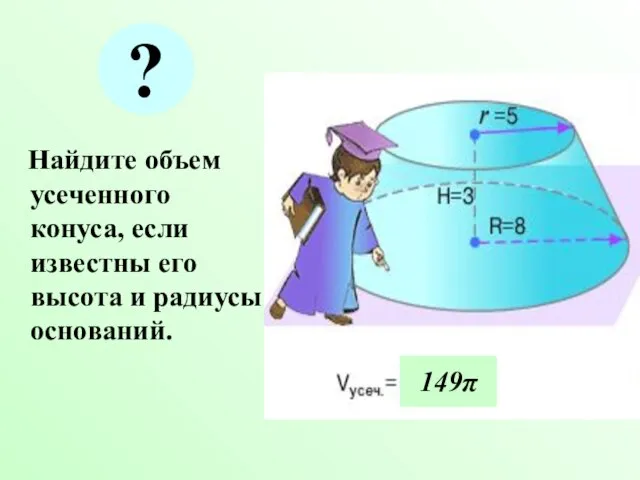
- 25. Найдите объем усеченного конуса, если известны его высота и радиусы оснований. 149π ?
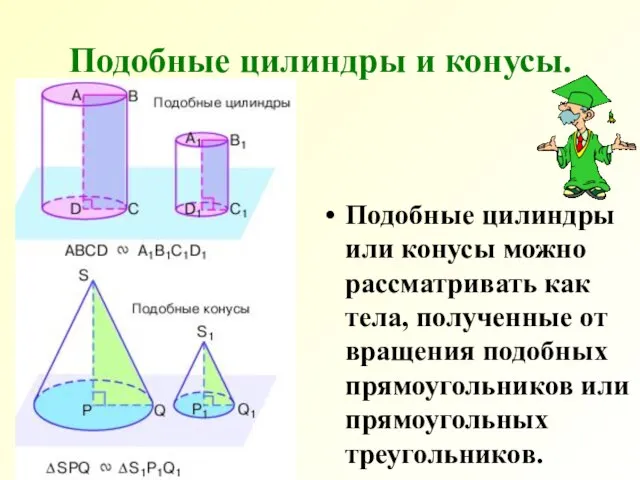
- 26. Подобные цилиндры и конусы. Подобные цилиндры или конусы можно рассматривать как тела, полученные от вращения подобных
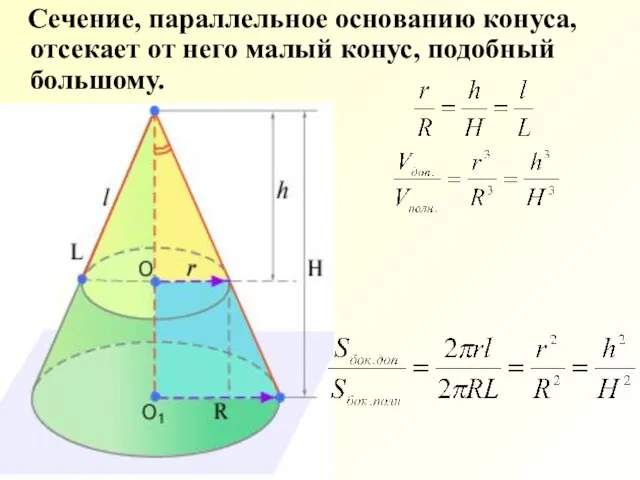
- 27. Сечение, параллельное основанию конуса, отсекает от него малый конус, подобный большому.
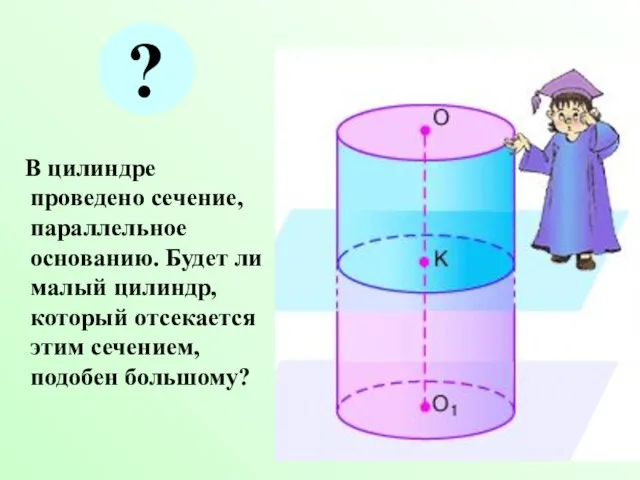
- 28. В цилиндре проведено сечение, параллельное основанию. Будет ли малый цилиндр, который отсекается этим сечением, подобен большому?
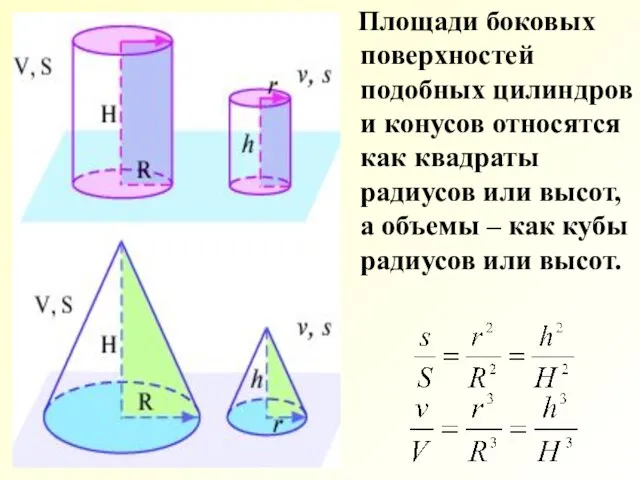
- 29. Площади боковых поверхностей подобных цилиндров и конусов относятся как квадраты радиусов или высот, а объемы –
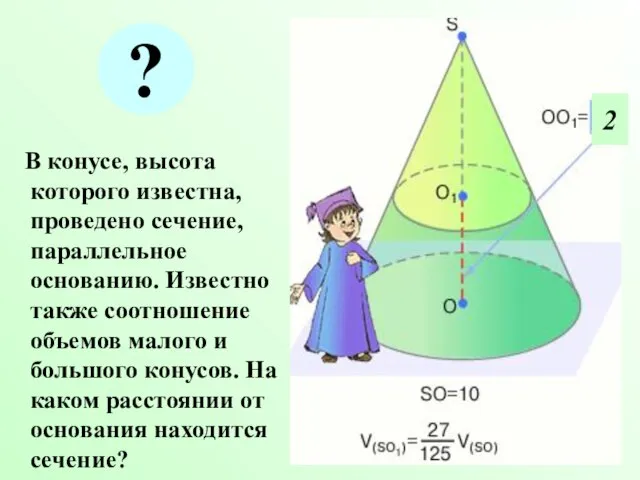
- 30. В конусе, высота которого известна, проведено сечение, параллельное основанию. Известно также соотношение объемов малого и большого
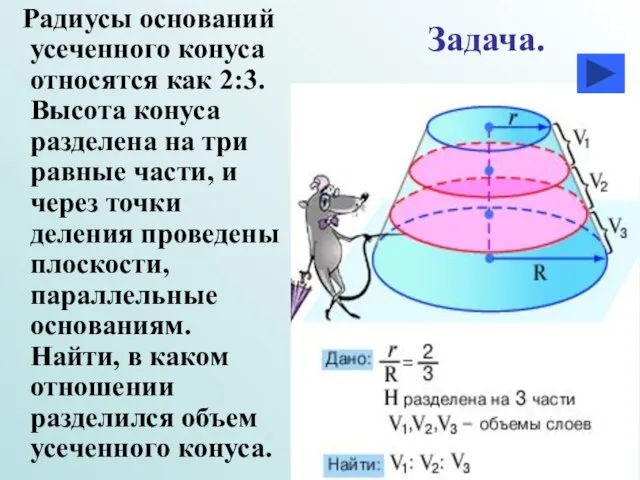
- 31. Радиусы оснований усеченного конуса относятся как 2:3. Высота конуса разделена на три равные части, и через
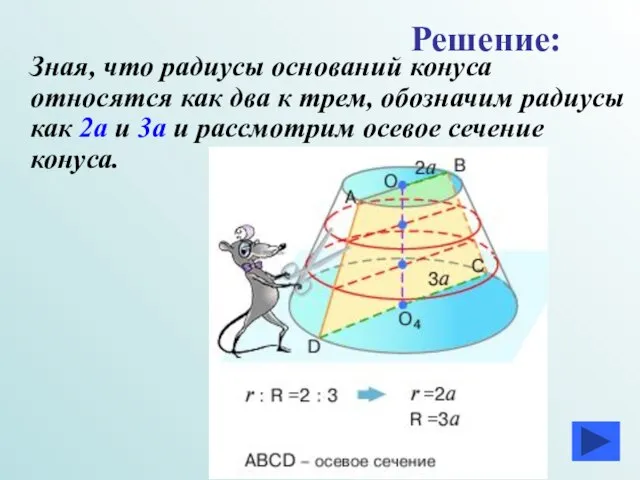
- 32. Зная, что радиусы оснований конуса относятся как два к трем, обозначим радиусы как 2а и 3а
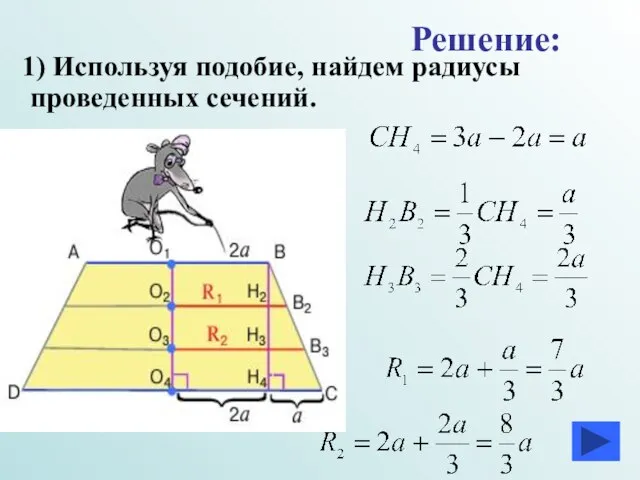
- 33. 1) Используя подобие, найдем радиусы проведенных сечений. Решение:
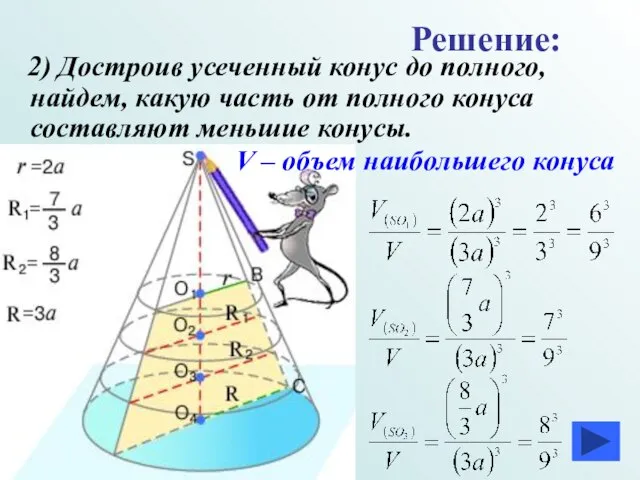
- 34. 2) Достроив усеченный конус до полного, найдем, какую часть от полного конуса составляют меньшие конусы. Решение:
- 36. Скачать презентацию





 Планы второго порядка
Планы второго порядка Формула перехода к новому основанию логарифма
Формула перехода к новому основанию логарифма Успешный ОГЭ: решаем устно. Урок геометрии, 9 класс
Успешный ОГЭ: решаем устно. Урок геометрии, 9 класс Умножение и деление десятичных дробей на натуральное число
Умножение и деление десятичных дробей на натуральное число Свойства функций
Свойства функций Иррациональные неравенства
Иррациональные неравенства Тригонометрические уравнения
Тригонометрические уравнения Исследование функций
Исследование функций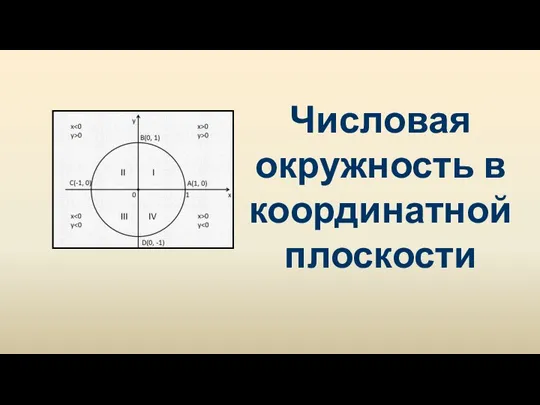 Числовая окружность в координатной плоскости
Числовая окружность в координатной плоскости Окружность, круг, их элементы и части. Центральный угол. 7 класс
Окружность, круг, их элементы и части. Центральный угол. 7 класс Функции и их графики
Функции и их графики Деление и умножение на 2
Деление и умножение на 2 Сумма углов треугольника
Сумма углов треугольника Тригонометрические уравнения
Тригонометрические уравнения Корни уравнения
Корни уравнения Презентация по математике "Дроби в Древнем Риме" -
Презентация по математике "Дроби в Древнем Риме" -  Сложение и вычитание однозначных чисел
Сложение и вычитание однозначных чисел Методология математического моделирования
Методология математического моделирования 7 задание из открытого банка ЕГЭ-2017
7 задание из открытого банка ЕГЭ-2017 Задания по математике (5 класс, часть 1)
Задания по математике (5 класс, часть 1) История развития экономико-математических методов (ЭММ) и моделей. Лекция 1
История развития экономико-математических методов (ЭММ) и моделей. Лекция 1 Соотношения между сторонами и углами треугольника
Соотношения между сторонами и углами треугольника Виды треугольников. 3 класс
Виды треугольников. 3 класс Линейные алгоритмы
Линейные алгоритмы Степенные, показательные, логарифмические и тригонометрические функции
Степенные, показательные, логарифмические и тригонометрические функции Функции. Область определения и множество значений; график функции; построение графиков функций, заданных различными способами
Функции. Область определения и множество значений; график функции; построение графиков функций, заданных различными способами Что? Где? Когда?
Что? Где? Когда? Комбинации многогранников и тел вращения
Комбинации многогранников и тел вращения