Содержание
- 2. Треугольник – геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, последовательно соединенных отрезками
- 3. Виды треугольников: остроугольные Тупоугольные прямоугольные
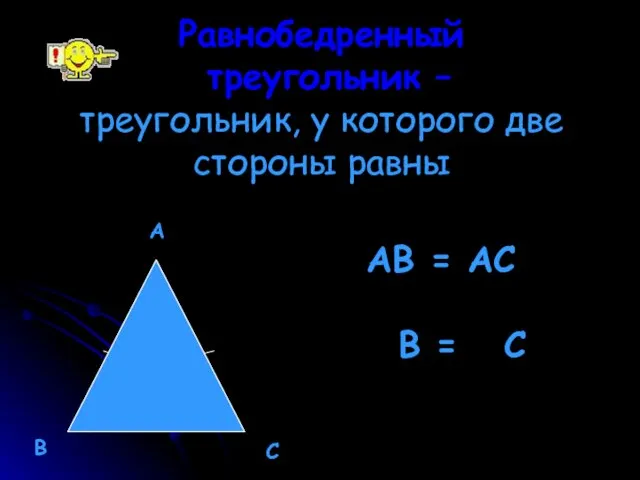
- 4. Равнобедренный треугольник – треугольник, у которого две стороны равны А В С АВ = АС B
- 5. Если два треугольника равны, то элементы одного треугольника соответственно равны элементам другого треугольника. В равных треугольниках
- 6. Первый признак равенства треугольников: Если две стороны и угол между ними одного треугольника соответственно равны двум
- 7. Второй признак равенства треугольников: Если сторона и два прилежащих к ней угла одного треугольника соответственно равны
- 8. Третий признак равенства треугольников: Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то
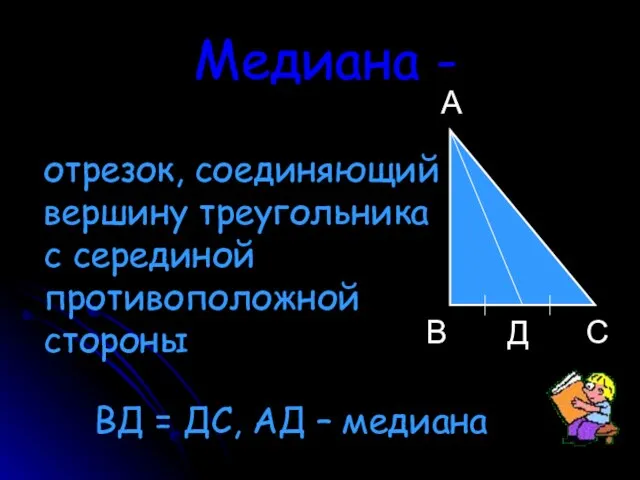
- 9. Медиана - отрезок, соединяющий вершину треугольника с серединой противоположной стороны А В С Д ВД =
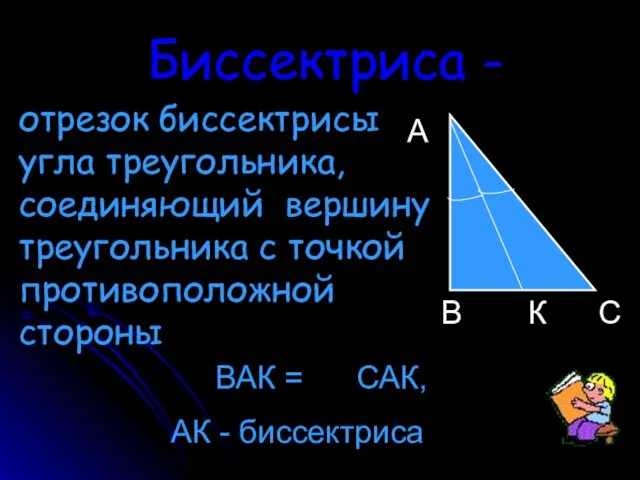
- 10. Биссектриса - отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны А В К
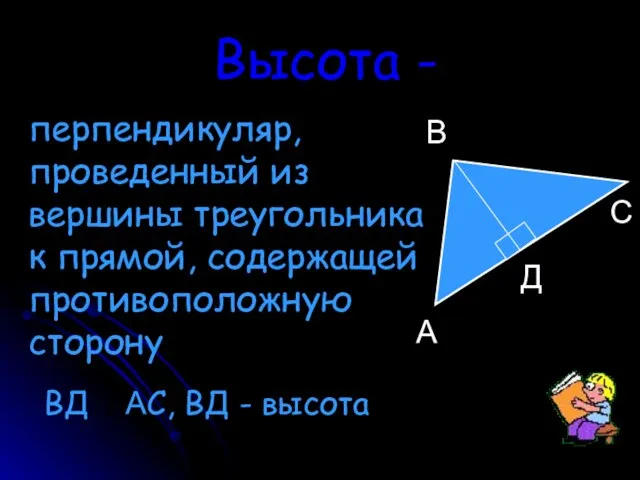
- 11. Высота - перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону А Д С В
- 12. В любом треугольнике медианы пересекаются в одной точке, биссектрисы пересекаются в одной точке, высоты или их
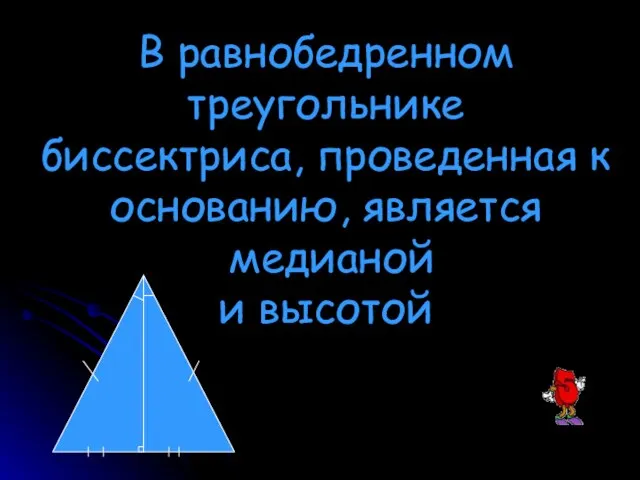
- 13. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой
- 14. Внешним углом треугольника называется угол, смежный с каким – нибудь углом этого треугольника Внешний Угол Внешний
- 15. Прямоугольный треугольник к а т е т к а т е т г и п о
- 16. Некоторые свойства прямоугольных треугольников сумма двух острых углов прямо- угольного треугольника равна 90° катет прямоугольного треуголь
- 17. Признаки равенства прямоугольных треугольников Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники
- 18. Признаки равенства прямоугольных треугольников если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и
- 19. Соотношение между сторонами и углами треугольника В треугольнике: 1) против большей стороны лежит больший угол; 2)
- 20. Неравенство треугольника Каждая сторона треугольника меньше суммы двух других сторон Для любых трех точек А, В
- 21. Построение треугольника по трем сторонам • • • C B A
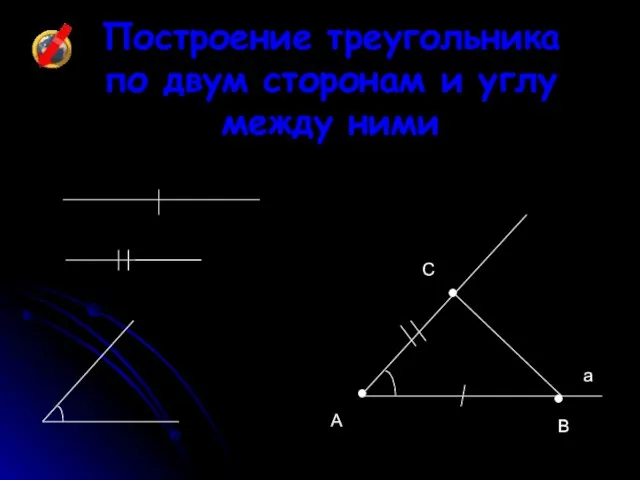
- 22. Построение треугольника по двум сторонам и углу между ними • • • A B C a
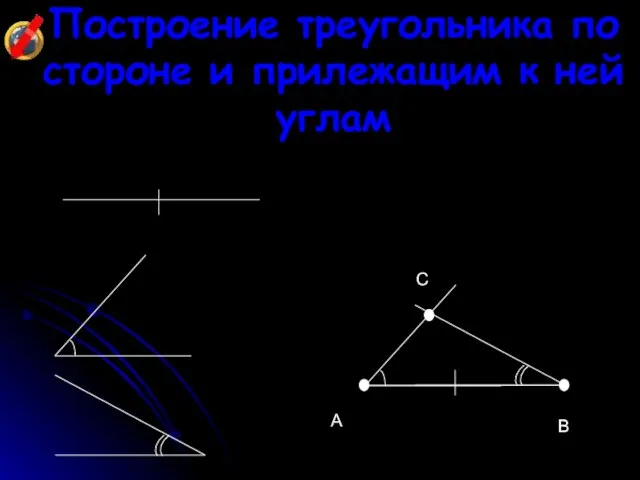
- 23. Построение треугольника по стороне и прилежащим к ней углам A B C
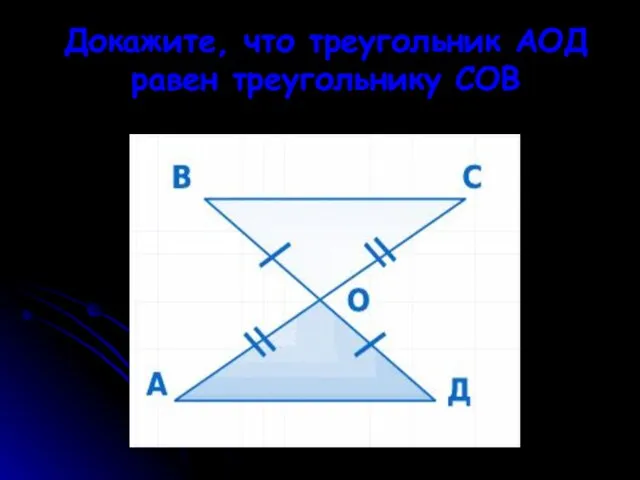
- 24. Докажите, что треугольник АОД равен треугольнику СОВ
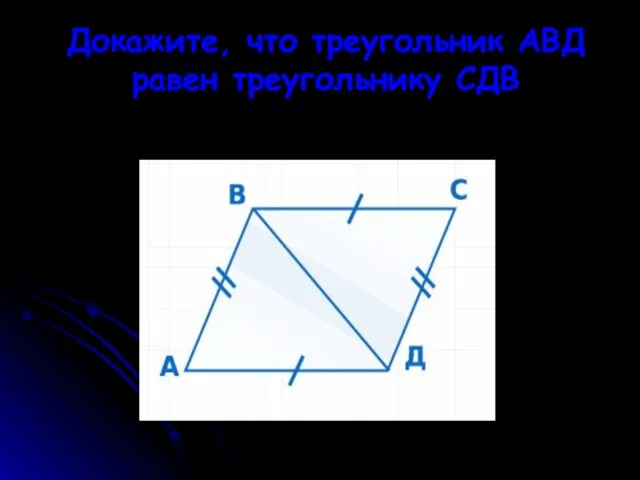
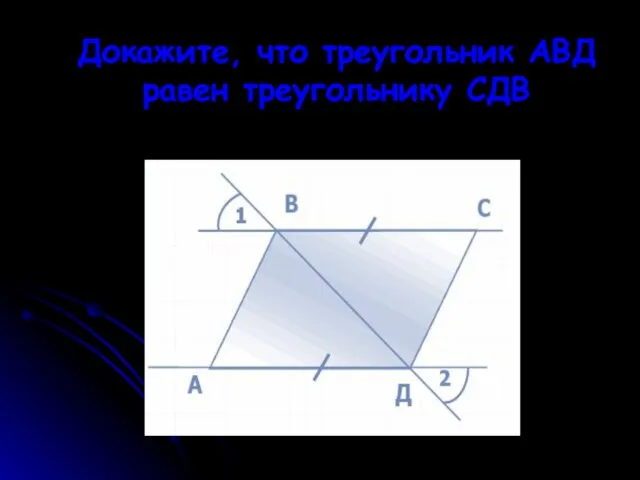
- 25. Докажите, что треугольник АВД равен треугольнику СДВ
- 26. Докажите, что треугольник АВД равен треугольнику СДВ
- 28. Скачать презентацию















 Планы второго порядка
Планы второго порядка Формула перехода к новому основанию логарифма
Формула перехода к новому основанию логарифма Успешный ОГЭ: решаем устно. Урок геометрии, 9 класс
Успешный ОГЭ: решаем устно. Урок геометрии, 9 класс Умножение и деление десятичных дробей на натуральное число
Умножение и деление десятичных дробей на натуральное число Свойства функций
Свойства функций Иррациональные неравенства
Иррациональные неравенства Тригонометрические уравнения
Тригонометрические уравнения Исследование функций
Исследование функций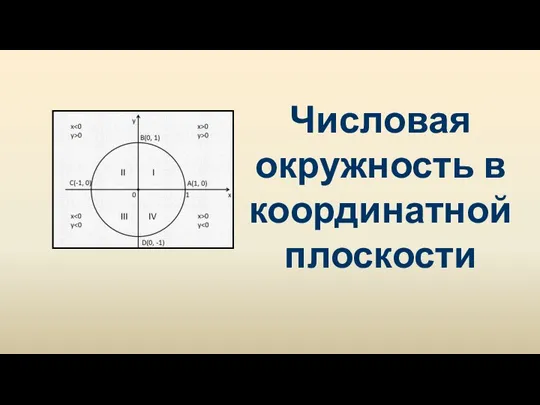 Числовая окружность в координатной плоскости
Числовая окружность в координатной плоскости Окружность, круг, их элементы и части. Центральный угол. 7 класс
Окружность, круг, их элементы и части. Центральный угол. 7 класс Функции и их графики
Функции и их графики Деление и умножение на 2
Деление и умножение на 2 Сумма углов треугольника
Сумма углов треугольника Тригонометрические уравнения
Тригонометрические уравнения Корни уравнения
Корни уравнения Презентация по математике "Дроби в Древнем Риме" -
Презентация по математике "Дроби в Древнем Риме" -  Сложение и вычитание однозначных чисел
Сложение и вычитание однозначных чисел Методология математического моделирования
Методология математического моделирования 7 задание из открытого банка ЕГЭ-2017
7 задание из открытого банка ЕГЭ-2017 Задания по математике (5 класс, часть 1)
Задания по математике (5 класс, часть 1) История развития экономико-математических методов (ЭММ) и моделей. Лекция 1
История развития экономико-математических методов (ЭММ) и моделей. Лекция 1 Соотношения между сторонами и углами треугольника
Соотношения между сторонами и углами треугольника Виды треугольников. 3 класс
Виды треугольников. 3 класс Линейные алгоритмы
Линейные алгоритмы Степенные, показательные, логарифмические и тригонометрические функции
Степенные, показательные, логарифмические и тригонометрические функции Функции. Область определения и множество значений; график функции; построение графиков функций, заданных различными способами
Функции. Область определения и множество значений; график функции; построение графиков функций, заданных различными способами Что? Где? Когда?
Что? Где? Когда? Комбинации многогранников и тел вращения
Комбинации многогранников и тел вращения