Содержание
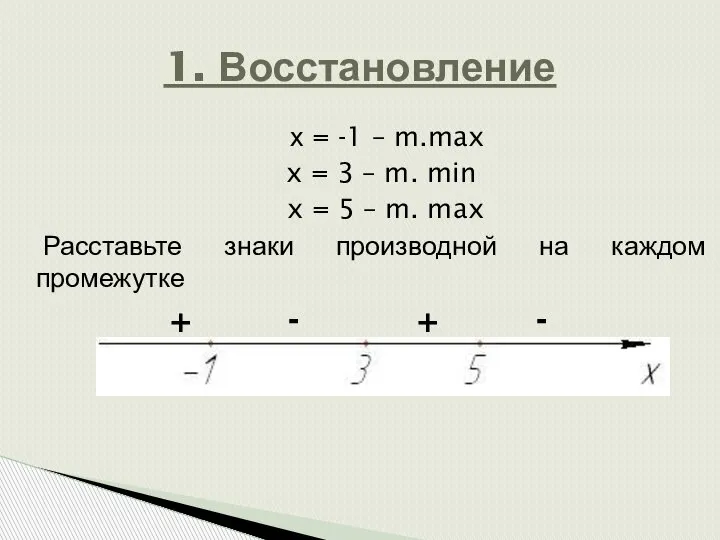
- 3. х = -1 – m.max x = 3 – m. min x = 5 – m.
- 4. х = -1 – m.max x = 3 – m. min x = 5 – m.
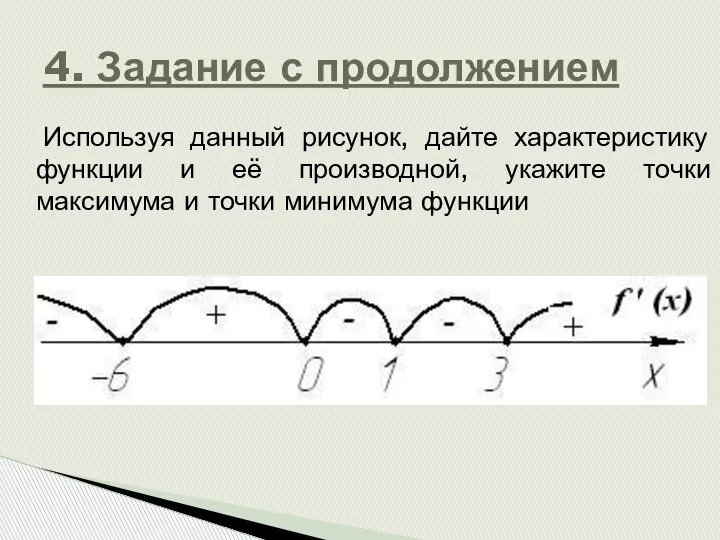
- 5. Используя данный рисунок, дайте характеристику функции и её производной, укажите точки максимума и точки минимума функции
- 6. Дан график функции y = f(x). Из данных утверждений выберите верные и неверные утверждения. Количество промежутков
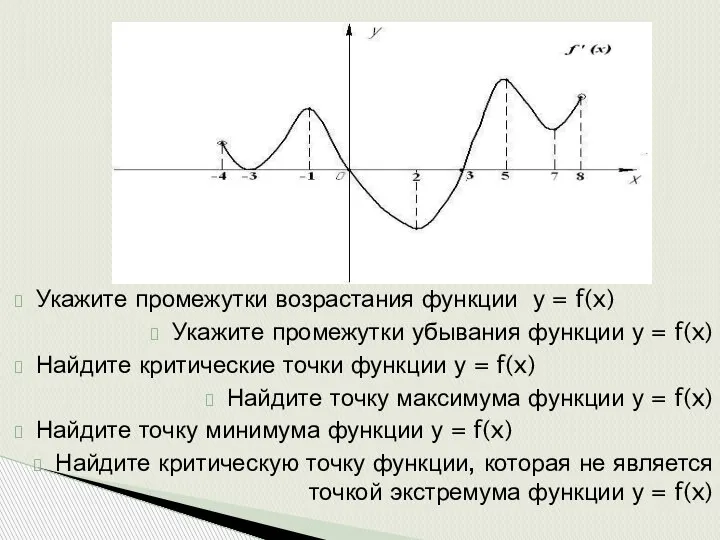
- 7. Укажите промежутки возрастания функции у = f(x) Укажите промежутки убывания функции у = f(x) Найдите критические
- 8. Простая я функция - это известно. Ещё расскажу, если вам интересно, Что точка экстремума есть у
- 10. Скачать презентацию




 Площадь прямоугольника
Площадь прямоугольника Алгоритм решения линейных уравнений
Алгоритм решения линейных уравнений Презентация на тему Сечения многогранников
Презентация на тему Сечения многогранников  Основы логики
Основы логики Решение иррациональных уравнений
Решение иррациональных уравнений Уравнение прямой. 9 класс
Уравнение прямой. 9 класс Решение задач. Многогранники. Тела вращения
Решение задач. Многогранники. Тела вращения Натуральные числа. Викторина
Натуральные числа. Викторина Применение графика производной к исследованию функции
Применение графика производной к исследованию функции Треугольник. Первый признак равенства треугольников
Треугольник. Первый признак равенства треугольников Презентация на тему Предел переменной величины
Презентация на тему Предел переменной величины  Презентация на тему Логарифмическая линия в ЕГЭ - 2011
Презентация на тему Логарифмическая линия в ЕГЭ - 2011  Кругові приклади
Кругові приклади Понятие логарифма
Понятие логарифма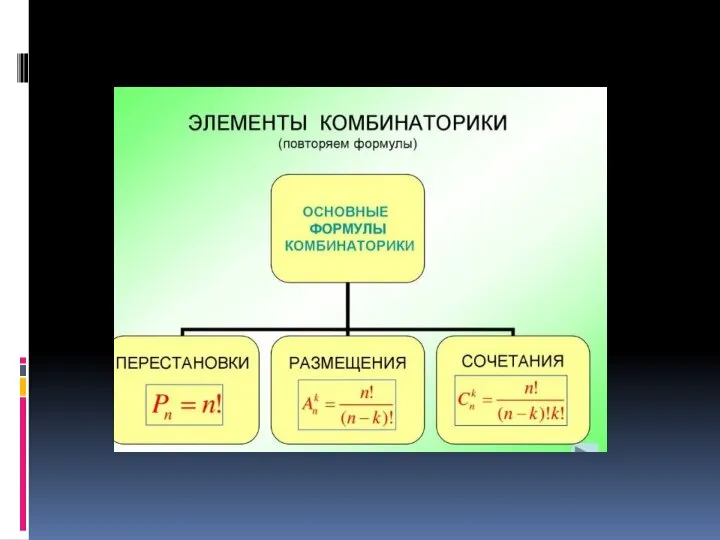 Основные понятия комбинаторики
Основные понятия комбинаторики График функции у = ах 2 + bх + qс
График функции у = ах 2 + bх + qс Решение задач на составление линейных алгоритмов
Решение задач на составление линейных алгоритмов Векторные задачи 1-го типа
Векторные задачи 1-го типа Применение игровых технологий на уроках математики в условиях внедрения ФГОС
Применение игровых технологий на уроках математики в условиях внедрения ФГОС Методы измерения физических величин
Методы измерения физических величин Определение перемещения
Определение перемещения Решение задач. 1 класс
Решение задач. 1 класс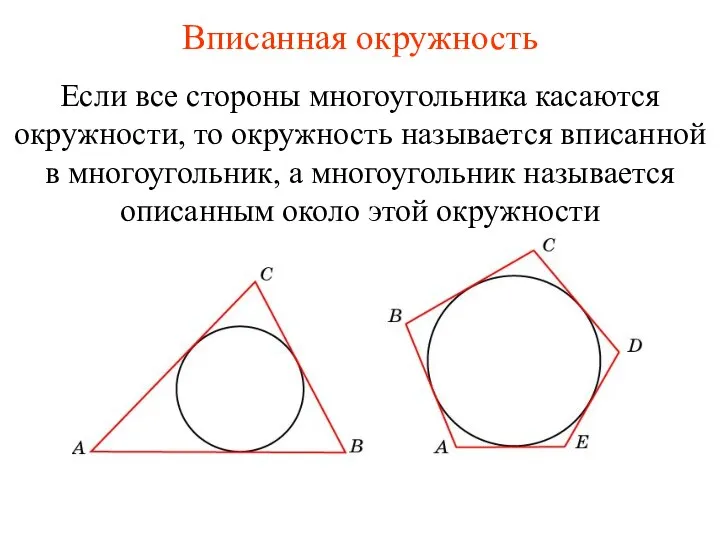 Вписанная окружность
Вписанная окружность Четные и нечётные функции
Четные и нечётные функции Таков многогранник
Таков многогранник Перпендикуляр и наклонная. Угол между прямой и плоскостью
Перпендикуляр и наклонная. Угол между прямой и плоскостью Сечение вокруг нас
Сечение вокруг нас Умножение дробей
Умножение дробей