Содержание
- 2. Существуют функции различные: Степенные и квадратичные. И названия их не прозаические- Логарифм и тригонометрические. Дополняют узы
- 3. Цели: Обобщить и систематизировать наши знания по теме. 2. Применять полученные знания, умения и навыки в
- 4. НАЙДИТЕ ПРОИЗВОДНУЮ 2 ответ 3 ответ 5) 4 ответ 5 ответ 1 ответ 4) 3) 2)
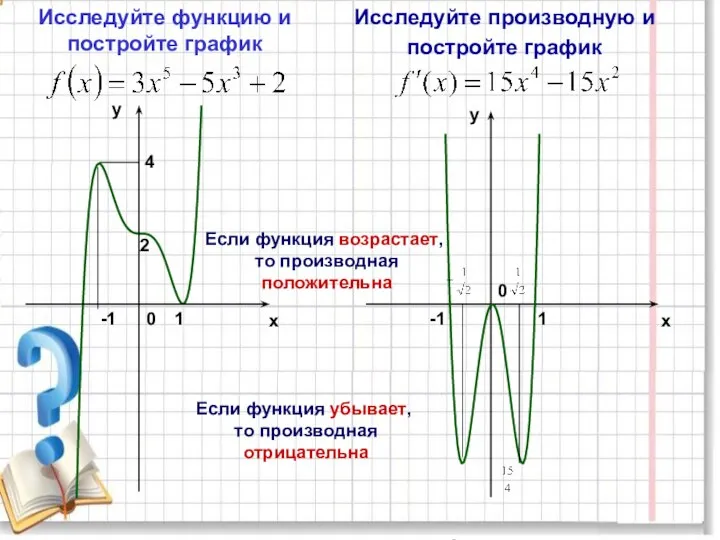
- 5. x y y x 2 -1 1 4 0 -1 1 0 Исследуйте функцию и постройте
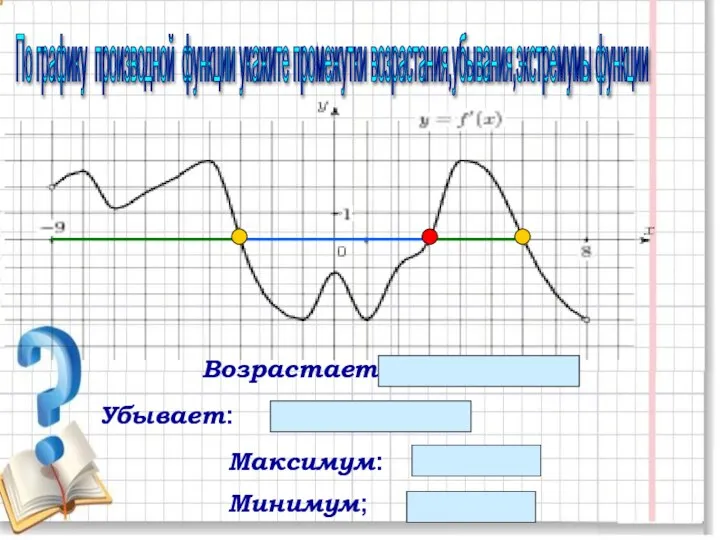
- 6. По графику производной функции укажите промежутки возрастания,убывания,экстремумы функции Максимум: - 3; 6 Минимум; 3 Возрастает: (-9;-3]
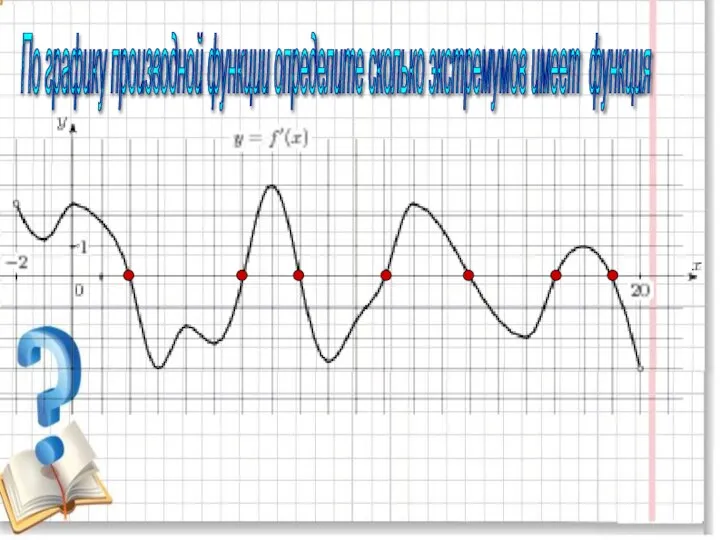
- 7. По графику производной функции определите сколько экстремумов имеет функция
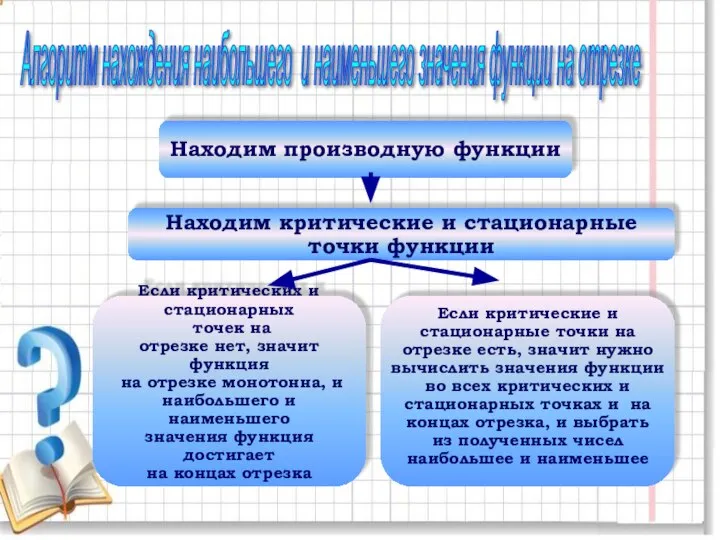
- 8. Алгоритм нахождения наибольшего и наименьшего значения функции на отрезке Находим производную функции Находим критические и стационарные
- 9. 1. 2. х = 1 ; х = 5/3 f(-1)=18 f(3) = 2 f(1) = 6
- 10. РЕШЕНИЕ:
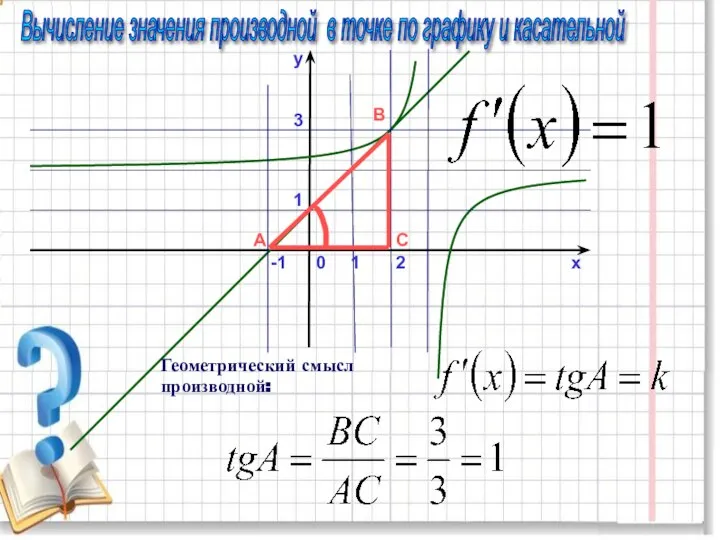
- 11. y x 0 1 2 -1 1 3 A B C Вычисление значения производной в точке
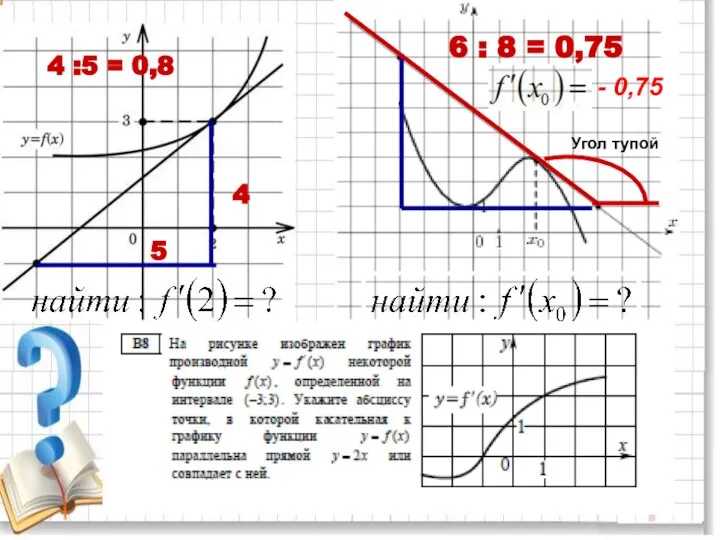
- 12. 4 5 4 :5 = 0,8 6 : 8 = 0,75 Угол тупой - 0,75
- 13. I вариант II вариант Найдите сумму экстремумов Найдите сумму экстремумов ] 1. 2. 2.
- 14. «Для меня сегодняшний урок…»
- 15. Выполнить тест «Задания ЕГЭ - В8, В11» Домашнее задание:
- 17. Скачать презентацию





![I вариант II вариант Найдите сумму экстремумов Найдите сумму экстремумов ] 1. 2. 2.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1058527/slide-12.jpg)


 Среднее арифметическое. Размах. Мода
Среднее арифметическое. Размах. Мода Векторная алгебра
Векторная алгебра Презентация на тему Формулы (5 класс)
Презентация на тему Формулы (5 класс)  Презентация на тему Исследование функции с помощью производной
Презентация на тему Исследование функции с помощью производной  Аксиомы стереометрии
Аксиомы стереометрии Оператор Лапласа в полярных, цилиндрических и сферических системах координат
Оператор Лапласа в полярных, цилиндрических и сферических системах координат Обработка экспериментальных данных. Многофакторная регрессия. Лекция 7
Обработка экспериментальных данных. Многофакторная регрессия. Лекция 7 Виды четырехугольников
Виды четырехугольников Цилиндр
Цилиндр Симметрия вокруг нас
Симметрия вокруг нас Несобственные интегралы. Геометрические приложения определенного интеграла
Несобственные интегралы. Геометрические приложения определенного интеграла Метод координат в пространстве
Метод координат в пространстве Презентация на тему Правила дифференцирования
Презентация на тему Правила дифференцирования  Состав числа 8
Состав числа 8 Учимся писать цифры
Учимся писать цифры Длина окружности и число пи
Длина окружности и число пи Геометрия, как наука
Геометрия, как наука Чётные и нечётные числа. Подготовка к контрольной работе
Чётные и нечётные числа. Подготовка к контрольной работе Многозначная логика
Многозначная логика Prezentatsia_Microsoft_PowerPoint(1)
Prezentatsia_Microsoft_PowerPoint(1) Вычислительная математика. Практика №1
Вычислительная математика. Практика №1 Координатная плоскость. Графики
Координатная плоскость. Графики Уравнение прямой
Уравнение прямой Презентация на тему Нахождение неизвестного по двум разностям
Презентация на тему Нахождение неизвестного по двум разностям  Теорема Фалеса
Теорема Фалеса Решение уравнений. Тест
Решение уравнений. Тест Методы многокритериальной оптимизации
Методы многокритериальной оптимизации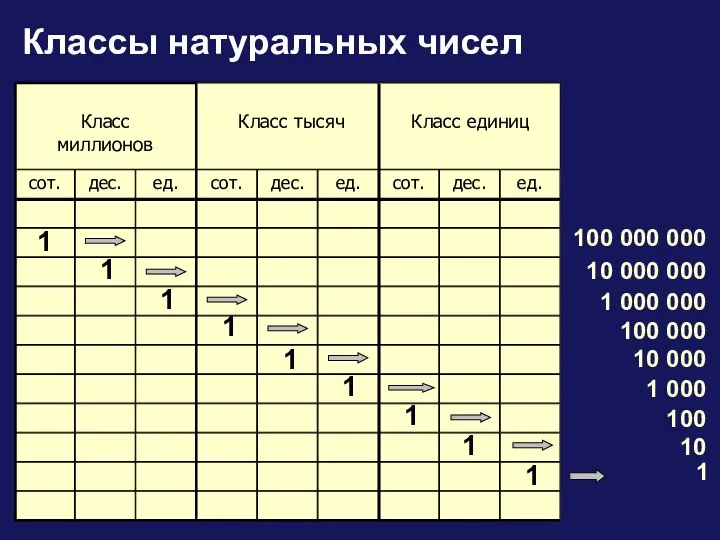 Классы натуральных чисел
Классы натуральных чисел