Применение векторного и смешанного произведений векторов в решении геометрических задач

Актуальность
Уменьшение времени на решение задач ЕГЭ, а так же других геометрических задач.
Более широкое применение координатно-векторного метода.
Уменьшается количество формул, которые необходимо выучить при подготовке к ЕГЭ.

Цели
Познакомиться с историей метода координат, изучить понятия векторного и смешанного произведения векторов, а так же области их применения
Задачи
Поиск, изучение и систематизация материалов по теме. Составление краткого наглядного учебного пособия для старшеклассников, посвященного методу координат в стереометрии.

Предмет исследования
Применение векторного и смешанного произведения векторов при решении геометрических задач методом координат.
Увеличение количества типов задач, решаемых методом координат с помощью использования векторного и смешанного произведений векторов.
Объект исследования
Векторное и смешанное произведения векторов. Метод координат

Гипотеза
Применяя такие понятия как векторное и смешанное произведения векторов, мы значительно экономим время и усилия на решение многих типов задач. Так же я предполагаю, что изучение метода координат выпускниками может стать очень полезным подспорьем при решении задачи 14 (С2) ЕГЭ.
5

Историческая справка
Александр Милетский – описывал широту и долготу места используя прямоугольные проекции
Гиппарх – идея опоясать карту земного шара параллелями и меридианами
Рене Декарт – теория метода координат, взаимопроникновение алгебры и геометрии
6

Вычисление определителей
Применение определителей
Формулы Крамера
Нахождение векторного и смешанного произведений векторов
7

Векторное произведение

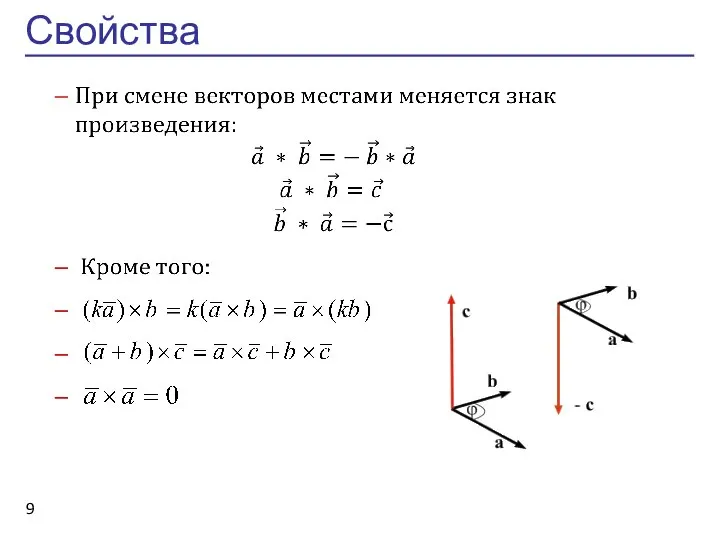
Свойства
9

Нахождение векторного произведения
10

Геометрический смысл
Длина векторного произведения – это площадь параллелограмма или удвоенная площадь треугольника.
11

Смешанное произведение

Свойства
1)
2)
3) три вектора компланарны тогда и только тогда, когда их смешанное произведение равно нулю

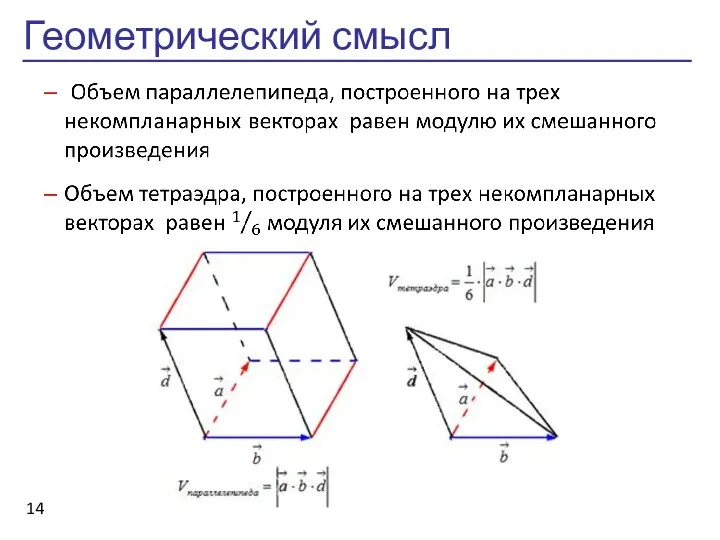
Геометрический смысл
14

Решение задачи С2
15

16