Содержание
- 2. Цели урока: Ввести понятие системы координат в пространстве. Выработать умение строить точку по заданным координатам и
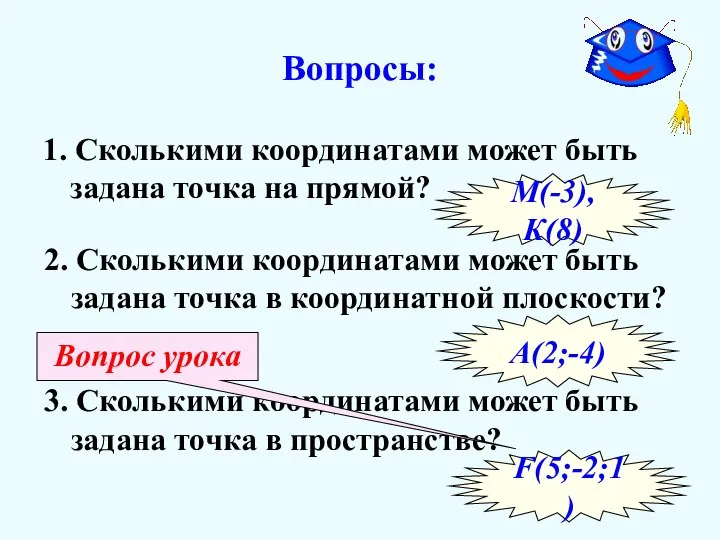
- 3. Вопросы: 1. Сколькими координатами может быть задана точка на прямой? М(-3), К(8) 2. Сколькими координатами может
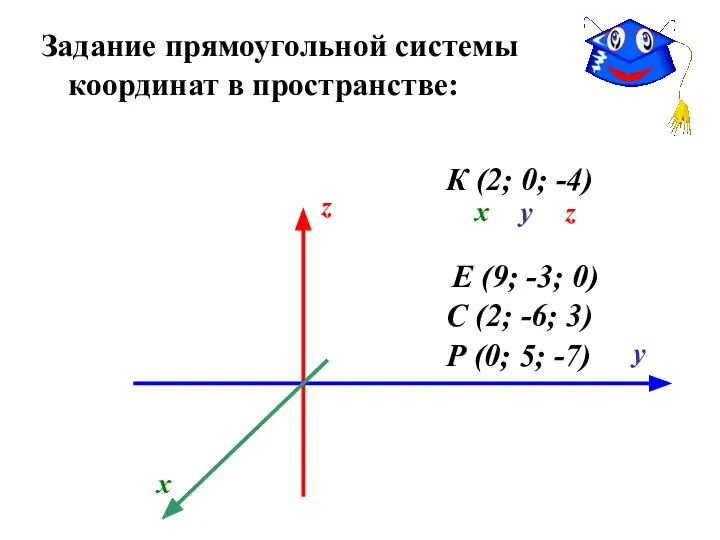
- 4. Задание прямоугольной системы координат в пространстве: Р (0; 5; -7) К (2; 0; -4) С (2;
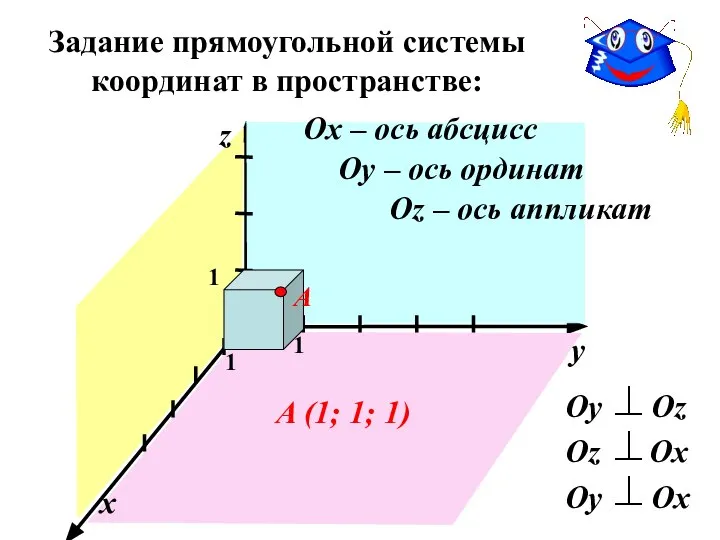
- 5. Задание прямоугольной системы координат в пространстве: О y Оy Оz Оz Оx Оy Оx x z
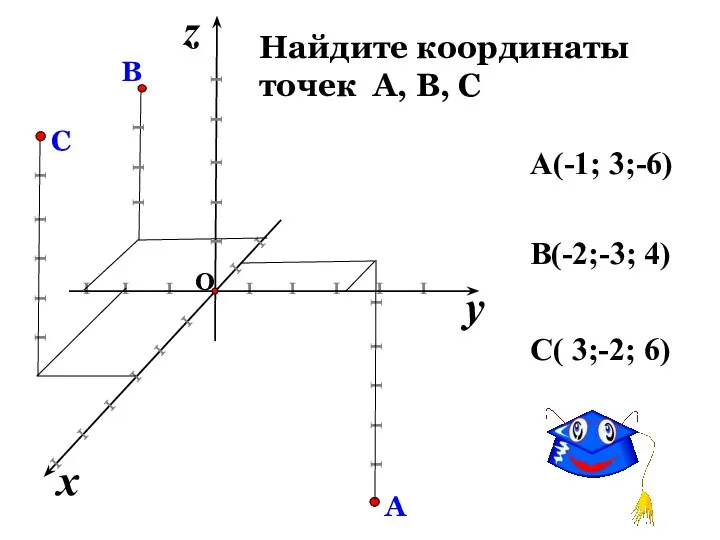
- 6. Найдите координаты точек А, В, С A(-1; 3;-6) B(-2;-3; 4) y x z I I I
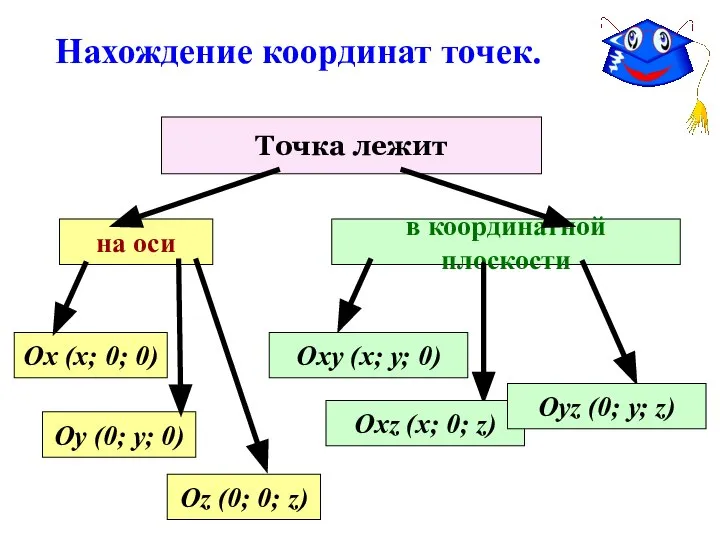
- 7. Нахождение координат точек. Точка лежит на оси Оу (0; у; 0) Ох (х; 0; 0) Оz
- 8. Решение задач. № 401 (а) Рассмотрим точку А (2; -3; 5) х у z 0 2
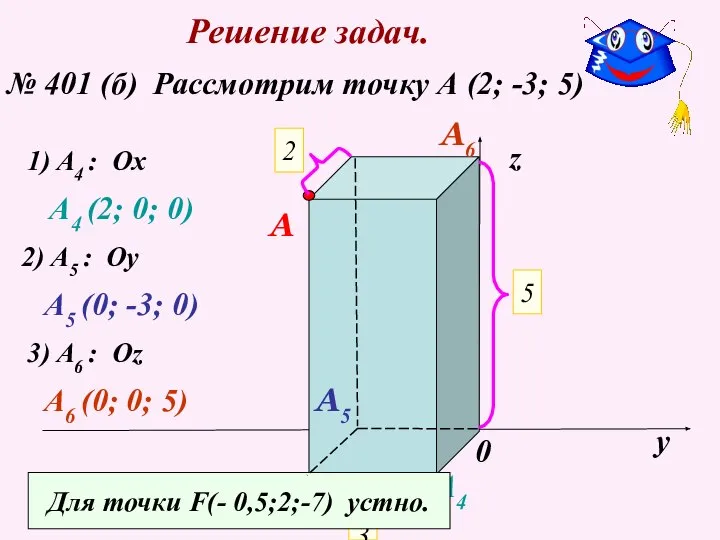
- 9. Решение задач. № 401 (б) Рассмотрим точку А (2; -3; 5) х у z 0 2
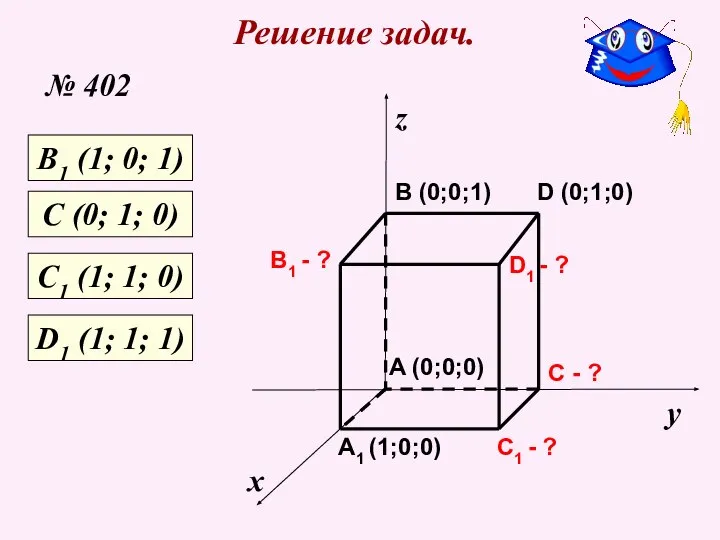
- 10. Решение задач. № 402 х у z C1 - ? C - ? A1 (1;0;0) B1
- 11. МОЛОДЦЫ!
- 12. Координаты вектора II этап урока
- 13. Цели этапа: Научиться раскладывать произвольный вектор по координатным векторам. Отработать навыки действий над векторами с заданными
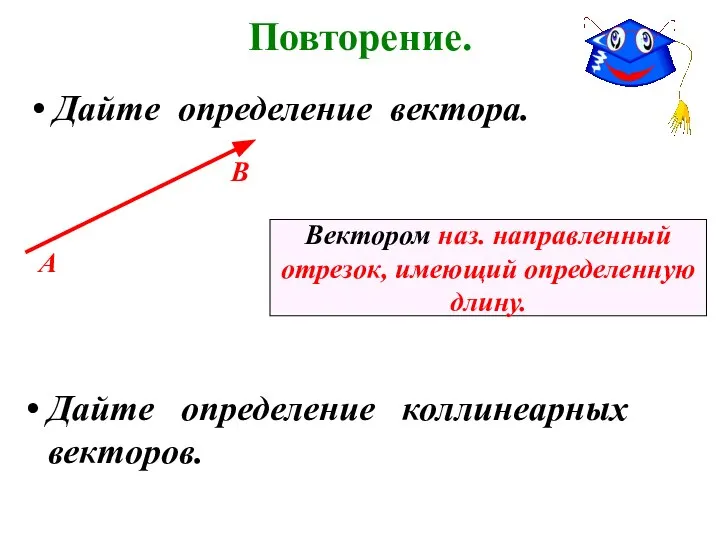
- 14. Повторение. Дайте определение вектора. А В Вектором наз. направленный отрезок, имеющий определенную длину. Дайте определение коллинеарных
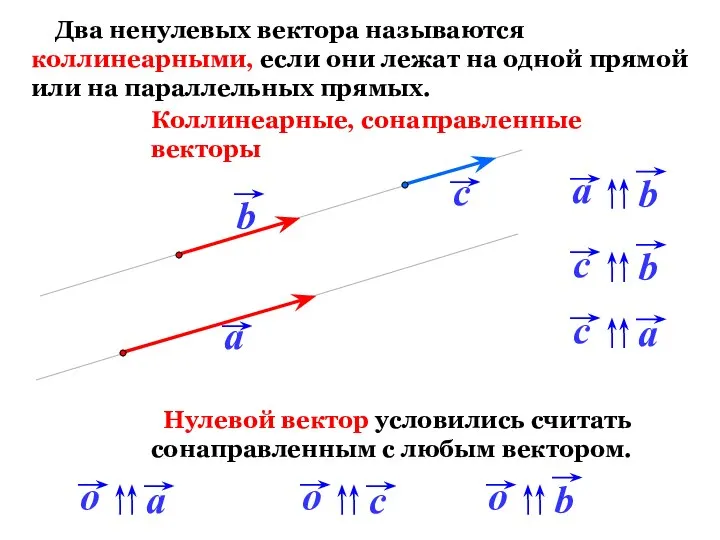
- 15. Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Коллинеарные,
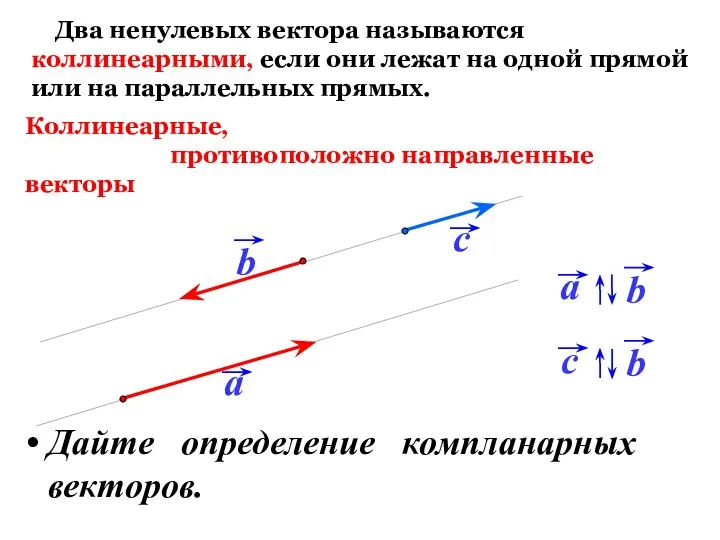
- 16. Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Коллинеарные,
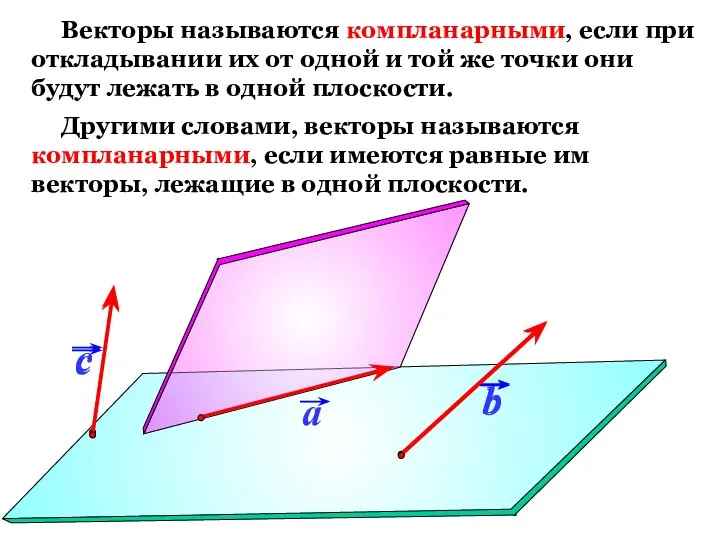
- 17. Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать
- 18. Любые два вектора компланарны. Три вектора, среди которых имеются два коллинеарных, также компланарны. Признак компланарности:
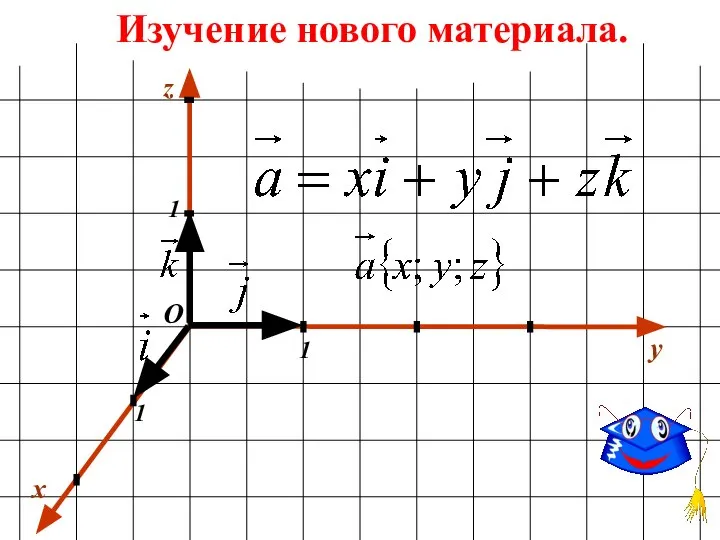
- 19. Изучение нового материала. x y 1 1 1 О z
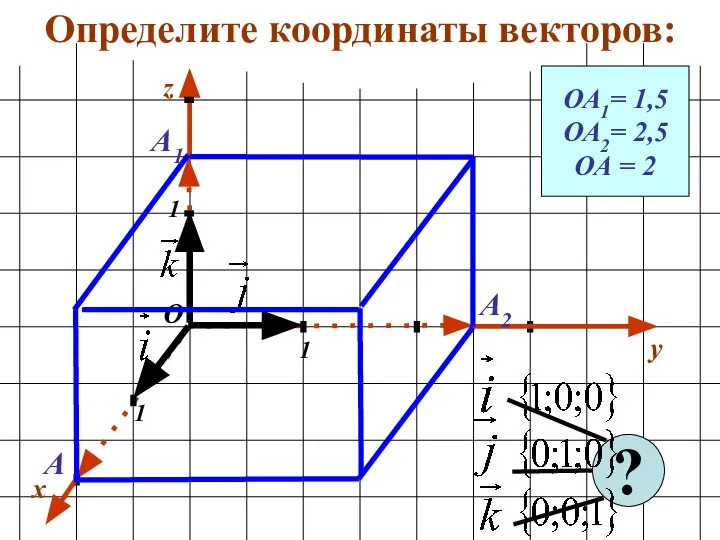
- 20. Определите координаты векторов: x y 1 1 1 О z ОА1= 1,5 ОА2= 2,5 ОА =
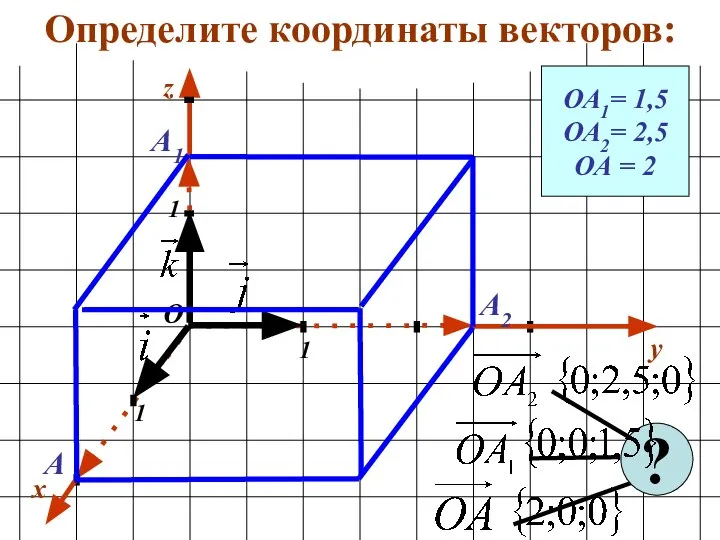
- 21. Определите координаты векторов: x y 1 1 1 О z ОА1= 1,5 ОА2= 2,5 ОА =
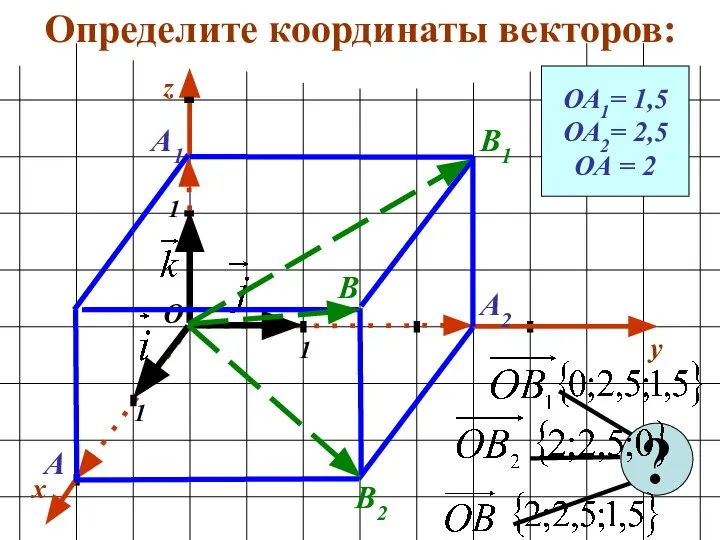
- 22. Определите координаты векторов: x y 1 1 1 О z ОА1= 1,5 ОА2= 2,5 ОА =
- 23. Разложите все векторы по координатным векторам. Проверяем:
- 24. Правила действий над векторами с заданными координатами. 1.Равные векторы имеют равные координаты. Пусть , х1 =
- 25. Правила действий над векторами с заданными координатами. 2. Каждая координата суммы двух (и более) векторов равна
- 26. Правила действий над векторами с заданными координатами. 3. Каждая координата произведения вектора на число равна произведению
- 27. Выполнить задание устно: Даны векторы: Найти вектор равный:
- 28. Письменно: Даны векторы: Найти координаты вектора: Ответ:
- 29. Домашнее задание: №№ 401(В,С), 407, 408 П. 42, 43 стр.116 в.1-6
- 30. Спасибо за урок!
- 31. Повторение. Даны точки: А (2; -1; 0) В (0; 0; -7) С (2; 0; 0) D
- 32. Выполнение задания с последующей проверкой. Начертить прямоугольную трехмерную систему координат и отметить в ней точки: А
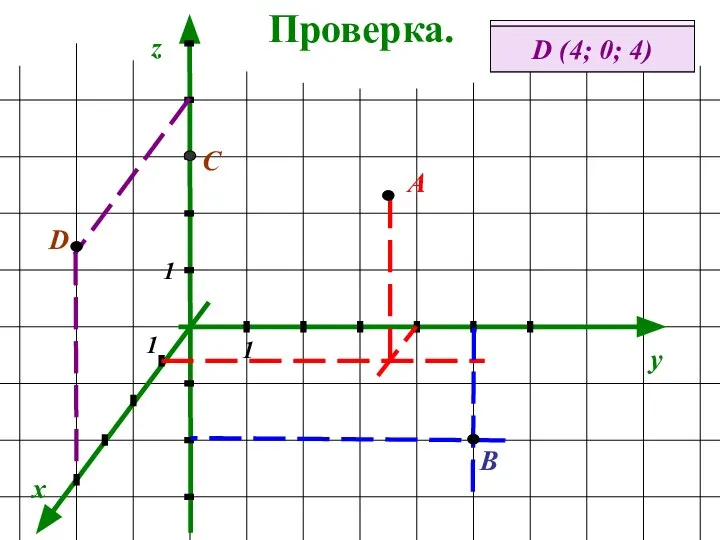
- 33. Проверка. x y z А (1; 4; 3) А В (0; 5; -3) 1 1 1
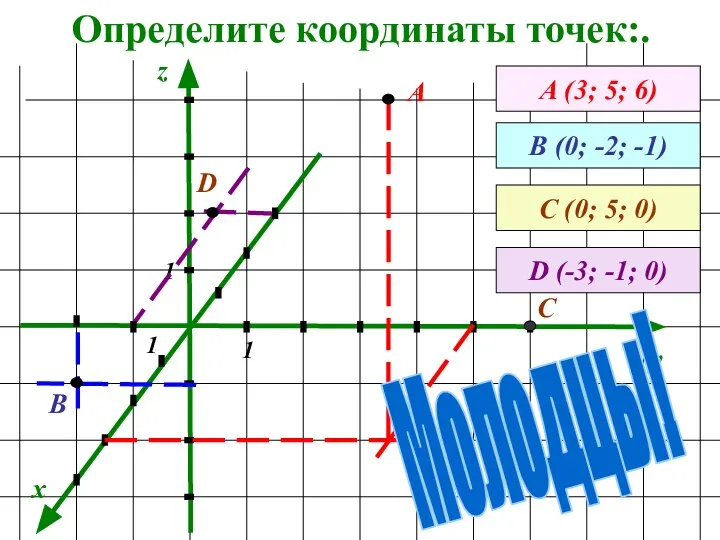
- 34. Определите координаты точек:. x y z А (3; 5; 6) А В (0; -2; -1) 1
- 35. Думаем… Отвечаем… Даны точки А (2; 4; 5), В (3; а; b), C (0; 4; d)
- 36. Повторение: 1. Даны точки А ( - 1; 7 ) и В ( 7; 1). а)
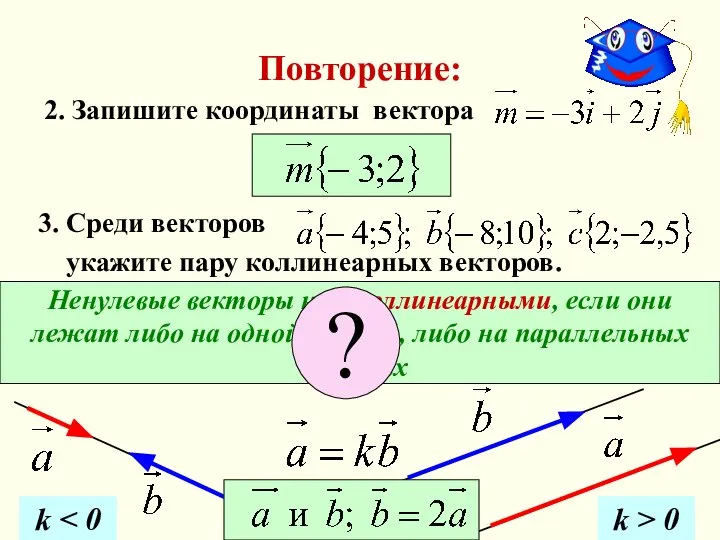
- 37. Повторение: 2. Запишите координаты вектора Ненулевые векторы наз. коллинеарными, если они лежат либо на одной прямой,
- 39. Скачать презентацию

















 Презентация на тему УРАВНЕНИЕ И ЕГО КОРНИ
Презентация на тему УРАВНЕНИЕ И ЕГО КОРНИ  Кругові приклади
Кругові приклади Презентация на тему Нужна ли в жизни координатная плоскость
Презентация на тему Нужна ли в жизни координатная плоскость  Метод интервалов. Решаем неравенства!
Метод интервалов. Решаем неравенства! Презентация на тему Элементы статистики
Презентация на тему Элементы статистики  Задачи по геометрии (6-7)
Задачи по геометрии (6-7) Десятичная запись дробных чисел (5 класс) - Презентация_
Десятичная запись дробных чисел (5 класс) - Презентация_ Двугранный угол
Двугранный угол Пирамида. Площади поверхностей. Объём. Многогранники
Пирамида. Площади поверхностей. Объём. Многогранники Презентация на тему Правильные многоугольники
Презентация на тему Правильные многоугольники  Умножение и деление отрицательных чисел. Урок-путешествие
Умножение и деление отрицательных чисел. Урок-путешествие Выполни вычисления
Выполни вычисления Калькуляционная карточка. Тесто заварное
Калькуляционная карточка. Тесто заварное Математка в жизни
Математка в жизни Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Аксиомы стереометрии. Следствия из аксиом
Аксиомы стереометрии. Следствия из аксиом Знаете ли вы... Высота, длина, вес
Знаете ли вы... Высота, длина, вес Уравнения и неравенства. Решение систем неравенств
Уравнения и неравенства. Решение систем неравенств Пропорции. Золотое сечение
Пропорции. Золотое сечение Понятие предиката и кванторы. Логические операции над предикатами
Понятие предиката и кванторы. Логические операции над предикатами Стереометрия. Многогранники
Стереометрия. Многогранники Вариационно-статистический метод анализа
Вариационно-статистический метод анализа Прямые и плоскости в пространстве
Прямые и плоскости в пространстве Матрицы. Определители. Лекция 1-2
Матрицы. Определители. Лекция 1-2 Несущая способность сечений при изгибе
Несущая способность сечений при изгибе Геометрический смысл производной
Геометрический смысл производной Влияние коэффициентов линейной функции на ее график
Влияние коэффициентов линейной функции на ее график Иррациональные уравнения. Открытый урок
Иррациональные уравнения. Открытый урок