Содержание
- 2. ПОМНИТЕ! Подготовка к ЕГЭ (В-4). Не забывайте делать проверку!
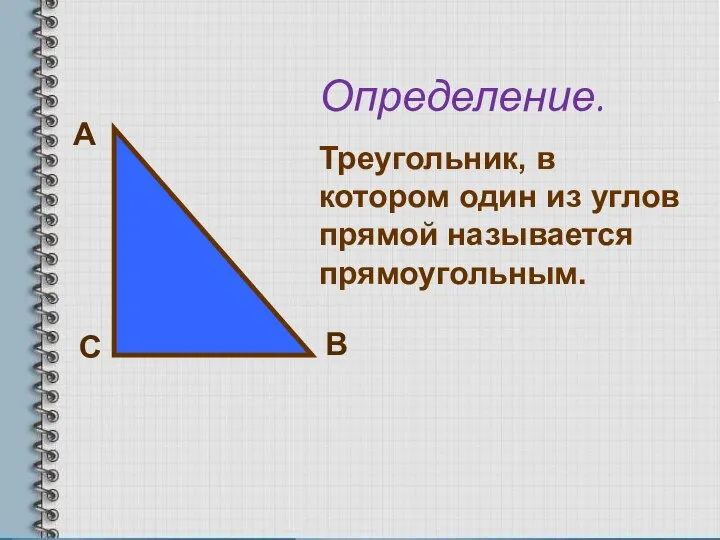
- 3. А С В Определение. Треугольник, в котором один из углов прямой называется прямоугольным.
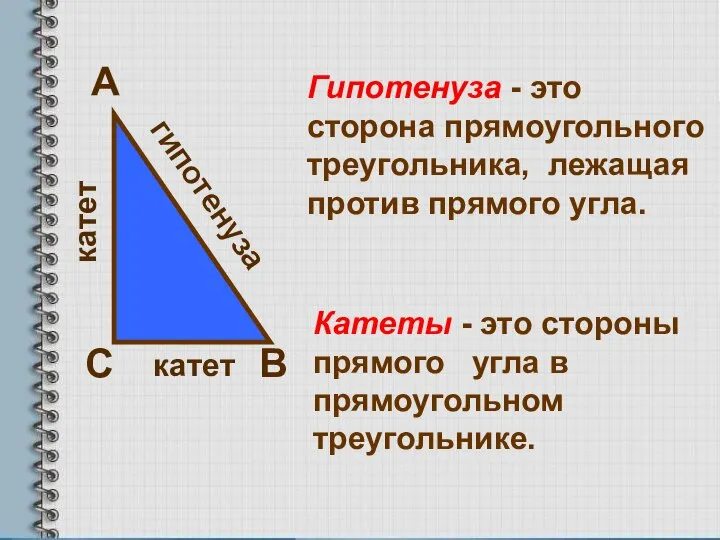
- 4. А В С катет катет гипотенуза Гипотенуза - это сторона прямоугольного треугольника, лежащая против прямого угла.
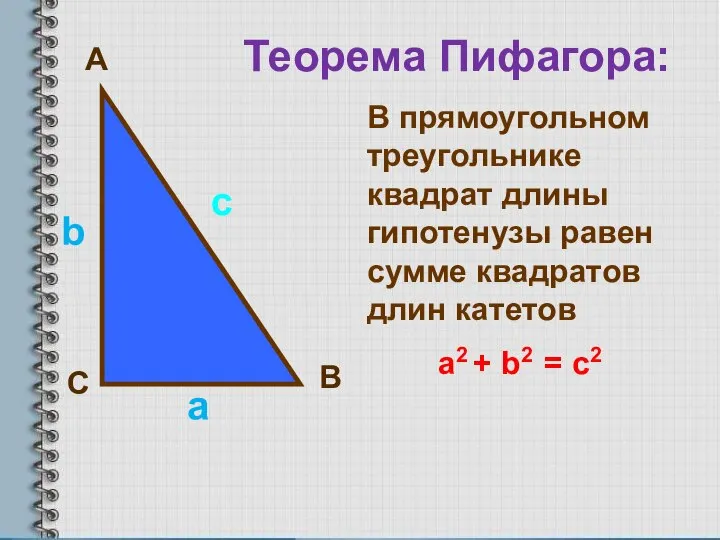
- 5. А С В Теорема Пифагора: В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов
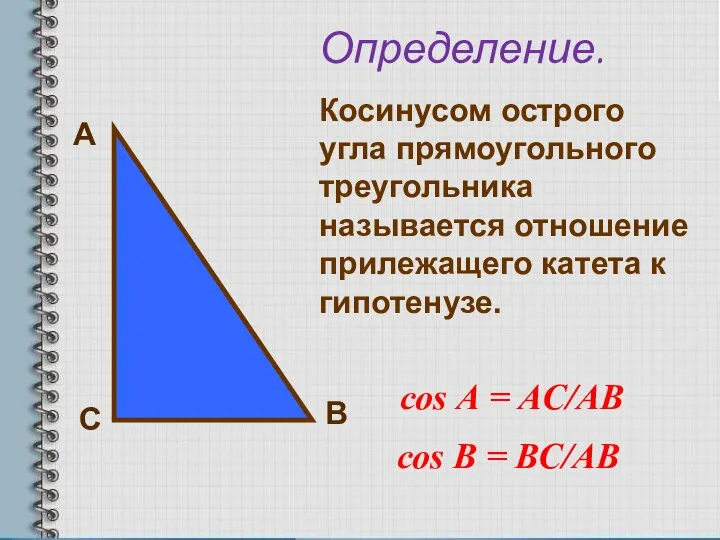
- 6. А С В Определение. Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. соs
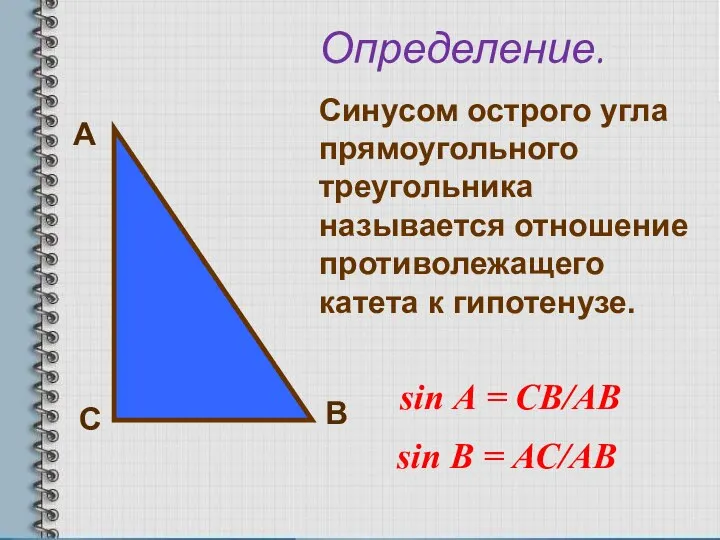
- 7. А С В Определение. Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. sin
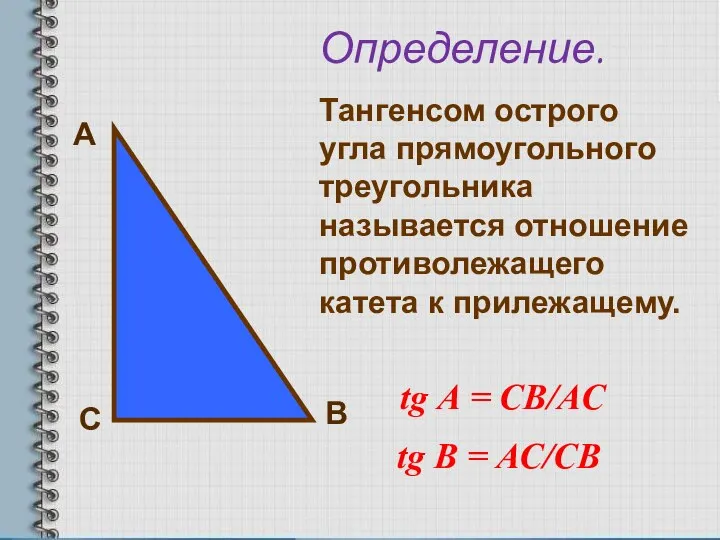
- 8. А С В Определение. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему. tg
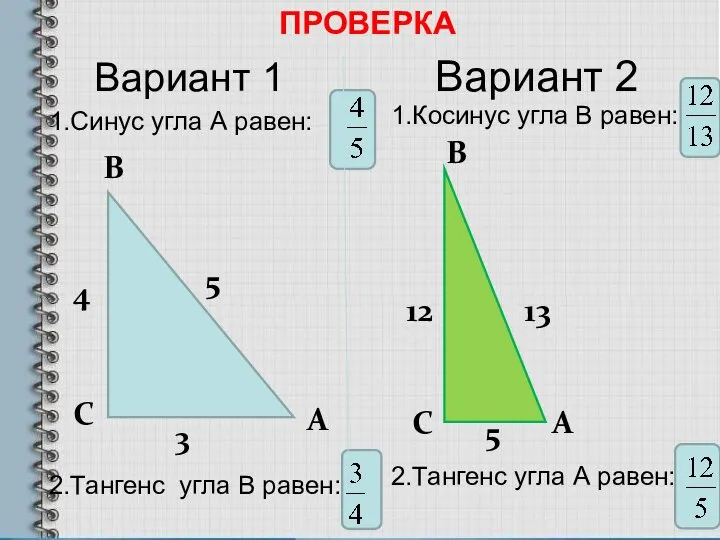
- 9. Вариант 1 1.Синус угла А равен: 2.Тангенс угла В равен: 1.Косинус угла В равен: 2.Тангенс угла
- 10. Пример 1. В треугольнике ABC угол C равен 90° , AB = 30, AC = 3
- 11. Пример 2. В равнобедренном треугольнике ABC с основанием AC боковая сторона AB равна 10, а высота,
- 12. Пример 3. В равнобедренном треугольнике ABC с основанием AC боковая сторона AB равна 17, а cos
- 13. Зачетные задания Проверь себя
- 14. 1. В треугольнике ABC угол C равен 90˚ , AB = 15, AC = 6 .
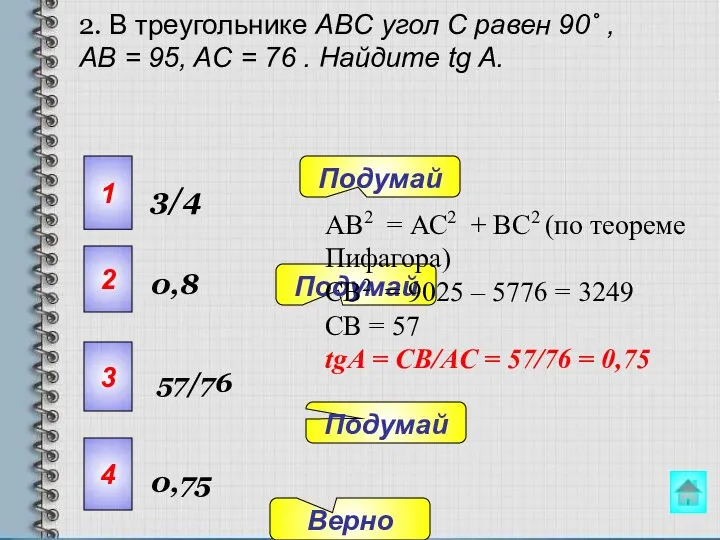
- 15. 2. В треугольнике ABC угол C равен 90˚ , AB = 95, AC = 76 .
- 16. 3. В треугольнике ABC угол C равен 90˚ , AC=10 , sin В = 5 /13.
- 18. Скачать презентацию







 Презентация на тему Сложение дробей с одинаковыми знаменателями (4 класс)
Презентация на тему Сложение дробей с одинаковыми знаменателями (4 класс)  Մաթեմատիկական_ինդուկցիայի_մեթոդը
Մաթեմատիկական_ինդուկցիայի_մեթոդը Теорема Пифагора
Теорема Пифагора Представление о ломаной линии и многоугольнике
Представление о ломаной линии и многоугольнике Переместительный закон умножения
Переместительный закон умножения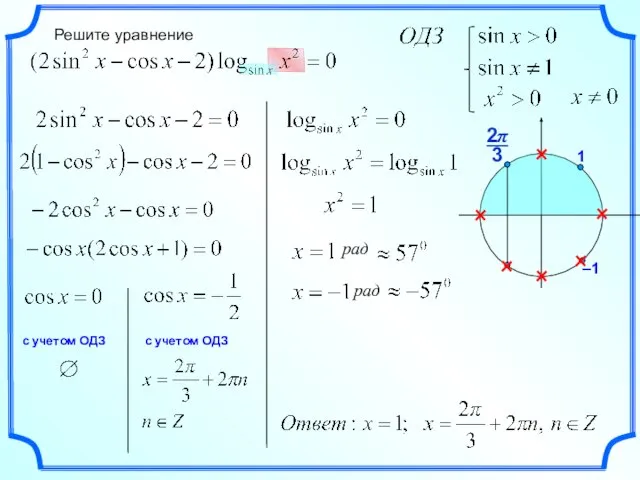 Решение уравнения
Решение уравнения Координаты вокруг нас
Координаты вокруг нас Подготовка к ОГЭ по математике
Подготовка к ОГЭ по математике Прятки с фигурами
Прятки с фигурами Элементы теории вероятности в практических задачах
Элементы теории вероятности в практических задачах Вычисление неопределенных интегралов методом интегрирования по частям
Вычисление неопределенных интегралов методом интегрирования по частям Устная нумерация чисел от 1 до 20
Устная нумерация чисел от 1 до 20 Все действия с десятичными дробями
Все действия с десятичными дробями Презентация на тему Периметр и площадь прямоугольника
Презентация на тему Периметр и площадь прямоугольника  Производная. Физический смысл производной. Приращение аргумента и приращение функции. Задания
Производная. Физический смысл производной. Приращение аргумента и приращение функции. Задания Презентация на тему Деятельностный подход в обучении на уроках математики
Презентация на тему Деятельностный подход в обучении на уроках математики  Симметрия в технике
Симметрия в технике Нахождение точек экстремума функции. 10 класс
Нахождение точек экстремума функции. 10 класс Решение системы линейных уравнений. Методы решения системы линейных уравнений
Решение системы линейных уравнений. Методы решения системы линейных уравнений Презентация на тему Прямоугольная система координат в пространстве (11 класс)
Презентация на тему Прямоугольная система координат в пространстве (11 класс)  Игра Верю - не верю
Игра Верю - не верю KomplanarnVektor
KomplanarnVektor Статистические гипотезы
Статистические гипотезы Решение задач на смеси и сплавы
Решение задач на смеси и сплавы Построение графиков функций с помощью производных
Построение графиков функций с помощью производных ИСТОРИЯ СИСТЕМ СЧИСЛЕНИЯ
ИСТОРИЯ СИСТЕМ СЧИСЛЕНИЯ Презентация на тему Виды симметрии. Центральная и осевая симметрия
Презентация на тему Виды симметрии. Центральная и осевая симметрия  Решение уравнений. Элективный курс. Алгебра 11 класс. Урок 1
Решение уравнений. Элективный курс. Алгебра 11 класс. Урок 1