Содержание
- 2. № 33.8(г)
- 3. № 33.9(г) Решите уравнение: t2 – 1 = 0 t2 – 12 = 0 (t –
- 4. № 33.10(г) Решите уравнение: 144z2 – 1 = 0 (12z)2 – 12 = 0 (12z –
- 5. № 33.33(а) Разложите многочлен на множители: (3х + 1)2 – (4х + 3)2 = = ((3х
- 6. № 33.34(а) Решите уравнение: Ответ: ± 0,8.
- 7. № 33.35(а) Решите уравнение: (2х – 5)2 – 36 = 0 (2х – 5)2 – 62
- 8. № 33.36(а) Решите уравнение: (а + 1)2 – (2а + 3)2 = 0 (а + 1
- 9. * К л а с с н а я р а б о т а. Разложение
- 10. РТ № 33.7 РТ № 33.8 х2 – х + 1 х2 + 3х + 9
- 11. РТ № 33.9 2p + 4q2 4p2 – 8pq2 + 16q4 3k2 + 5n2 9k4 –
- 12. РТ № 33.10 9a2 – 12ab + 16b2 4a2 – 10ab + 25b2
- 13. РТ № 33.11 3х2 – 4у 9х4 + 12х2у + 16у2 7n2 – 3m2 49n4 +
- 14. РТ № 33.12 16a2 + 12ab + 9b2 4a2 + 6ab + 9b2
- 15. РТ № 33.13 (х + у)(х2 – ху + у2) = (2с – 6d)((2c)2 + 2c·6d
- 16. РТ № 33.13 = (2p + 4q2)((2p)2 – 2p·4q2 + (4q2)2) = = (2p + 4q2)(4p2
- 17. РТ № 33.14 2а 3b 4n 5k 6y 7x 8k 9m d2 t3 0,4c3d4 0,1s6t6
- 18. РТ № 33.15 (2а)3 – (4n)3 = = (2а – 4n)((2а)2 + 2а·4n + (4n)2) =
- 19. РТ № 33.15 (4n)3 – (7x)3 = = (4n – 7x)((4n)2 + 4n·7x + (7x)2) =
- 20. РТ № 33.16 27n3 – 8 = (3n)3 – 23 = = (3n – 2)((3n)2 +
- 21. РТ № 33.16 (5ху)3 – z3 = = (5ху – z)((5ху)2 + 5ху·z + z2) =
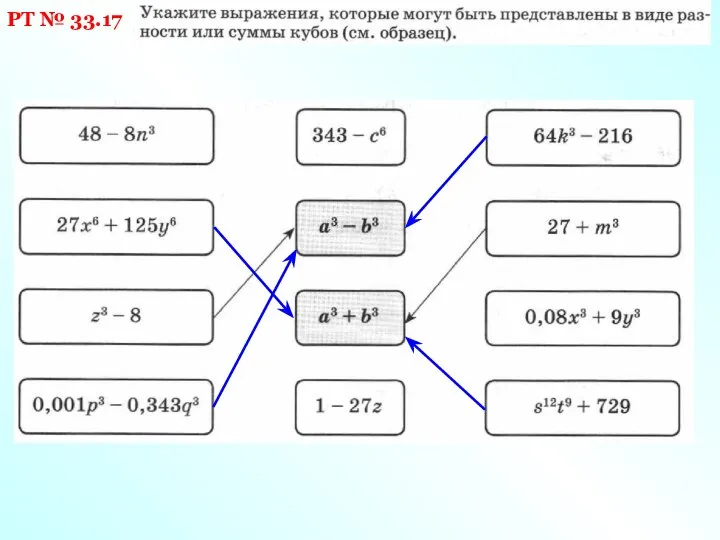
- 22. РТ № 33.17
- 23. РТ № 33.18 = 33 + m3 = (3 + m)(9 – 3m + m2) =
- 24. РТ № 33.18 = (s4t3)3 + 93 = = (s4t3 + 9)(s8t6 – 9s4t3 + 81)
- 25. Дома: У: стр. 139 § 33 З: § 33 № 11 – 18(б).
- 27. Скачать презентацию























 Математические понятия и их виды
Математические понятия и их виды Презентация на тему Решение задач с помощью квадратных уравнений
Презентация на тему Решение задач с помощью квадратных уравнений  Проецирование многогранных и кривых поверхностей
Проецирование многогранных и кривых поверхностей Динамическое программирование
Динамическое программирование Ур3
Ур3 Переместительное свойство умножения
Переместительное свойство умножения Матрицы и действия над ними
Матрицы и действия над ними Закрепление. Повтори правила стр. 72, 74
Закрепление. Повтори правила стр. 72, 74 Прямая в пространстве R3. Лекция 6
Прямая в пространстве R3. Лекция 6 Единицы измерения площадей
Единицы измерения площадей Второй признак равенства треугольников. Теорема
Второй признак равенства треугольников. Теорема Проценты
Проценты 3D моделирование на уроках стереометрии
3D моделирование на уроках стереометрии Дискретные случайные величины
Дискретные случайные величины Великие математики
Великие математики тригонометрия 1 урок
тригонометрия 1 урок Угол и биссектриса
Угол и биссектриса Сжатие(растяжение) графика вдоль оси ординат
Сжатие(растяжение) графика вдоль оси ординат Свойства определенных интегралов
Свойства определенных интегралов 2_5321245475066619345
2_5321245475066619345 Урок математики во 2 классе
Урок математики во 2 классе Презентация на тему Задачи с практическим содержанием по теме "Арифметическая и геометрическая прогрессии"
Презентация на тему Задачи с практическим содержанием по теме "Арифметическая и геометрическая прогрессии"  Презентация на тему Разность и её значение (1 класс)
Презентация на тему Разность и её значение (1 класс)  Десятичные дроби в разных профессиях. 6 класс
Десятичные дроби в разных профессиях. 6 класс Сравнение чисел
Сравнение чисел Основы функционального анализа
Основы функционального анализа Population statistical methods
Population statistical methods Составные задачами, новые способы решения
Составные задачами, новые способы решения