Содержание
- 2. Основные понятия Общий вид системы линейных уравнений (СЛУ) с тремя неизвестными: где - неизвестные переменные, -
- 3. Методы решения СЛУ с тремя неизвестными Метод обратной матрицы 2) Метод Крамера
- 4. Метод обратной матрицы Метод применим, когда число уравнений системы равно числу переменных и определитель матрицы системы
- 5. Метод обратной матрицы В матричной форме записи эта система уравнений имеет вид т.е Пусть . Тогда
- 6. Пример1: Решите СЛУ матричным способом Решение: Перепишем систему уравнений в матричной форме: Так как то систему
- 7. Решите систему матричным методом: Построим обратную матрицу с помощью матрицы из алгебраических дополнений элементов матрицы :
- 8. Решите систему матричным методом: Осталось вычислить матрицу неизвестных переменных, умножив обратную матрицу на матрицу-столбец свободных членов:
- 9. Метод Крамера Пусть нам требуется решить систему трёх линейных уравнений с тремя неизвестными: (1) в которой
- 10. Решите систему методом Крамера: Решение: Вычислим определитель системы: Так как определитель системы отличен от нуля, то
- 12. Скачать презентацию









 Презентация на тему Преобразование плоскости
Презентация на тему Преобразование плоскости  Процент. Понятие процента
Процент. Понятие процента Проверочная работа по теме Кровь
Проверочная работа по теме Кровь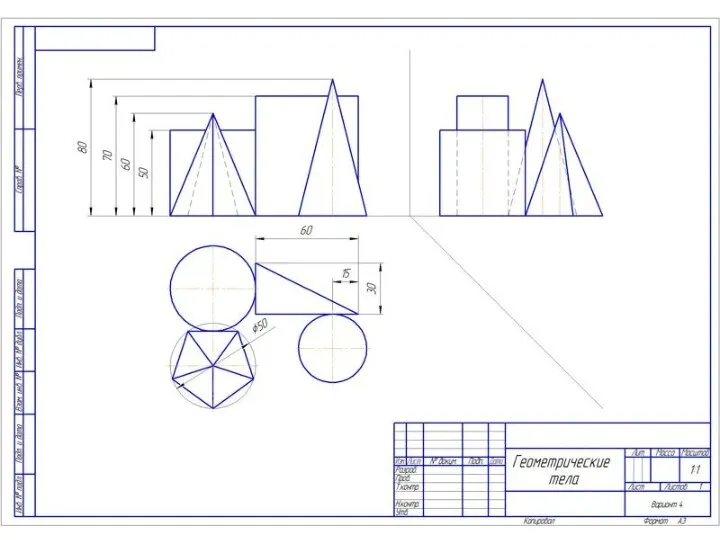 Геометрические тела. 9 класс
Геометрические тела. 9 класс Геометрические приложения определенного интеграла
Геометрические приложения определенного интеграла Комбинаторика. Решение задач
Комбинаторика. Решение задач Межлабораторные сравнительные испытания и сличения
Межлабораторные сравнительные испытания и сличения Элементы математической статистики. Лекция 1
Элементы математической статистики. Лекция 1 Умножение чисел столбиком (5 класс)
Умножение чисел столбиком (5 класс) Интересные факты в тригонометрии
Интересные факты в тригонометрии Упражнения
Упражнения Решение задач. Штрих Шеффера
Решение задач. Штрих Шеффера Решаем примеры
Решаем примеры Площадь треугольника и высоты
Площадь треугольника и высоты Тригонометрические уравнения и методы их решений
Тригонометрические уравнения и методы их решений Измерение отрезков и углов
Измерение отрезков и углов Согласование подходов к проверке заданий с развернутым ответом. Задания 22, 25
Согласование подходов к проверке заданий с развернутым ответом. Задания 22, 25 Векторы в пространстве. Тест
Векторы в пространстве. Тест Решение дробно-рациональных уравнений. Урок 2
Решение дробно-рациональных уравнений. Урок 2 Логарифмическая линия в ЕГЭ
Логарифмическая линия в ЕГЭ Числовые и буквенные выражения
Числовые и буквенные выражения Действительные числа
Действительные числа Временные ряды
Временные ряды Окружность и круг. Повторение 7 класс
Окружность и круг. Повторение 7 класс Презентация на тему Конус. Сечение конуса плоскостями
Презентация на тему Конус. Сечение конуса плоскостями  Инструкция по изготовлению трубогранника. Тетраэдр
Инструкция по изготовлению трубогранника. Тетраэдр Формулы приведения
Формулы приведения Материалы по теме Окружность и углы
Материалы по теме Окружность и углы