Слайд 2На зачет:
НА ЛР:
РАБОЧАЯ ТЕТРАДЬ С ШАБЛОНОМ ОТЧЕТА (ФОРМАТ А4)
НОУТБУК (ОДИН НА ДВОИХ)

С MULTISIM 12.0 ИЛИ ВЫШЕ
Слайд 3Опр. (БСЭ) Схемотехника — научно-техническое направление, охватывающее проблемы проектирования и исследования схем

электронных устройств радиотехники и связи, вычислительной техники, автоматики и др. областей техники.
Опр. (Науч.-техн. Словарь) Схемотехника - научно-техническое направление, охватывающее проблемы анализа и синтеза электронных устройств радиотехники, связи, автоматики, вычислит. техники с целью обеспечения оптимального выполнения ими заданных функций.
Слайд 4Основная задача: синтез (определение структуры) электронных схем, обеспечивающих выполнение определенных функций и

расчет параметров, входящих в них элементов
Слайд 5Взаимное соответствие функций алгебры логики и логических схем
ОСНОВНЫЕ ПОЛОЖЕНИЯ АЛГЕБРЫ ЛОГИКИ
В отличие

от аналоговых электронных устройств, в цифровых устройствах (ЦУ) входные и выходные сигналы могут принимать ограниченное количество состояний. В соответствии с логическим соглашением (ГОСТ 2.743-82), в зависимости от конкретной физической реализации элементов ЦУ, более положительному значению физической величины, "H" - уровень, соответствует состояние "логическая 1", а менее положительному значению ,"L - уровень" - "логический 0". Такое соглашение называется положительной логикой. Обратное соотношение называется отрицательной логикой. В ГОСТ'е 19480 - 89 даны наименования, определения и условные обозначения основных параметров и характеристик цифровых микросхем.
Слайд 6Взаимное соответствие функций алгебры логики и логических схем
Теоретической основой проектирования ЦУ является алгебра-логики или

булева алгебра, оперирующая логическими переменными. Для логических переменных, принимающих только два значения, существуют 4 основных операции. Операция логическое "И" (AND) конъюнкция или логическое умножение, обозначается * или /\. Операция логическое "ИЛИ" (OR), дизъюнкция или логическое сложение, обозначается + или \/ . Операция логическое "НЕ" (NOT), изменение значения, инверсия или отрицание, обозначается чертой над логическим выражением. Инверсия иногда будет в тексте обозначаться знаком " ~ ". Операция эквивалентности обозначается "=".
Слайд 7АКСИОМЫ
Из (1, 2) и (1',2') следует: x + x = x и

x * x = x. (5)
Из (1, 3) и (2',3') следует: x + 0 = x и 0 * x = 0. (6)
Из (2, 3) и (1',3') следует: 1 + x = 1 и x * 1 = x. (7)
Из (3) и (3') следует: x +~x = 1 и~x * x = 0. (8)
Из (4) и (4') следует: ~(~x) = x. (9)
Слайд 8Взаимное соответствие функций алгебры логики и логических схем
из (1,1'), (2,2'), (3,3') и

(4,4') следует:
~( x0+x1 ) = ~x0 * ~x1 и ~( x0 * x1) = ~x0 + ~x1 . (10)
Последние выражения (10) называют принципом двойственности или теоремой
Де Моргана (инверсия логической суммы равна логическому произведению инверсий и наоборот). Соотношения двойственности для n переменных, часто записывают в виде:
~(x1 + .. + xn) = ~x1 * . .* ~xn и
~(x1 * .. * xn) = ~x1 + .. + ~xn (11)
Слайд 9Взаимное соответствие функций алгебры логики и логических схем
На функции И и ИЛИ

распространяются обычные алгебраические законы - переместительный, сочетательный и распределительный, которые легко доказываются методом перебора:
x1 op x0 = x0 op x1 - переместительный,
x2 op x1 op x0 = (x2 op x1) op x0 - сочетательный
x2*(x1+x0) = (x2*x1) + (x2*x0) и x2 + (x1*x0) = (x2+x1) * (x2+x0) – распределительный
, где операция op может быть, либо И, либо ИЛИ. Наряду с тремя основными логическими функциями, называемыми также переключательными, существуют и другие.
Слайд 10Взаимное соответствие функций алгебры логики и логических схем
ПЕРЕКЛЮЧАТЕЛЬНЫЕ ФУНКЦИИ
Для n - логических

переменных (аргументов) существует 2n их комбинаций или двоичных наборов. На каждом таком наборе может быть определено значение функции 0 или 1. Если значения функции отличаются хотя бы на одном наборе, функции - разные. Общее число переключательных функций (ПФ) от n аргументов равно N=22n. Для n=2, N=16. При n=3, N=256 и далее очень быстро растет. Практическое значение имеют 16 функций от 2-х переменных, т.к. любое сложное выражение можно рассматривать как композицию из простейших.
Слайд 11Взаимное соответствие функций алгебры логики и логических схем

Слайд 12Взаимное соответствие функций алгебры логики и логических схем
ЗАПОМНИТЕ СЛЕДУЮЩИЕ ОПРЕДЕЛЕНИЯ. Функция "И"

равна единице, если равны единице ВСЕ ее аргументы. Функция "ИЛИ" равна единице, если равен единице ХОТЯ БЫ один аргумент. Функция "ИСКЛЮЧАЮЩЕЕ ИЛИ" (XOR) равна единице, если равен единице ТОЛЬКО один ее аргумент.











 Решение дифференциальных уравнений методом ломаных Эйлера с использованием электронных таблиц MS Excel
Решение дифференциальных уравнений методом ломаных Эйлера с использованием электронных таблиц MS Excel Ряды распределения в статистике
Ряды распределения в статистике Отношение. Пропорция
Отношение. Пропорция Элементы теории вероятности
Элементы теории вероятности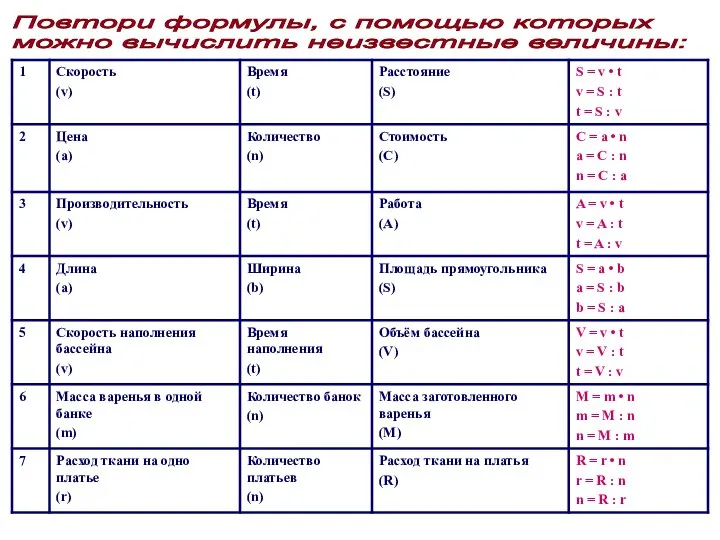 Скорость (v), Время (t), Расстояние (S)
Скорость (v), Время (t), Расстояние (S) Аксиомы стереометрии. Некоторые следствия из аксиом
Аксиомы стереометрии. Некоторые следствия из аксиом Вокруг квадратного трёхчлена
Вокруг квадратного трёхчлена Старинные задачи с использованием дробей
Старинные задачи с использованием дробей Центральные углы и углы, вписанные в окружность
Центральные углы и углы, вписанные в окружность Тройные интегралы в цилиндрических координатах
Тройные интегралы в цилиндрических координатах Структура урока
Структура урока Стереометрия. Многогранники
Стереометрия. Многогранники Презентация на тему Натуральные числа
Презентация на тему Натуральные числа  Основы факторного моделирования безопасности систем вида защита – объект – среда
Основы факторного моделирования безопасности систем вида защита – объект – среда Понятие логарифма
Понятие логарифма Евклид. Детство и ранние годы
Евклид. Детство и ранние годы Презентация на тему Делители и кратные
Презентация на тему Делители и кратные  Подготовка к ЕГЭ. Графическое решение уравнений и неравенств
Подготовка к ЕГЭ. Графическое решение уравнений и неравенств Станция Игровая. Занимательная математика
Станция Игровая. Занимательная математика Готовимся к ЕГЭ. Базовый уровень
Готовимся к ЕГЭ. Базовый уровень Позиция 7 ЕГЭ 2016. Физический смысл производной
Позиция 7 ЕГЭ 2016. Физический смысл производной Оценки параметров распределения. Статистические оценки
Оценки параметров распределения. Статистические оценки Пример проектной работы. Зимние олимпийские игры. Общая статистика
Пример проектной работы. Зимние олимпийские игры. Общая статистика Векторная алгебра. Лекция 4
Векторная алгебра. Лекция 4 Тригонометрические уравнения и математические термины на английском языке
Тригонометрические уравнения и математические термины на английском языке Решение задач Параллельные прямые
Решение задач Параллельные прямые Однозначные и двузначные числа
Однозначные и двузначные числа Операции над графами
Операции над графами