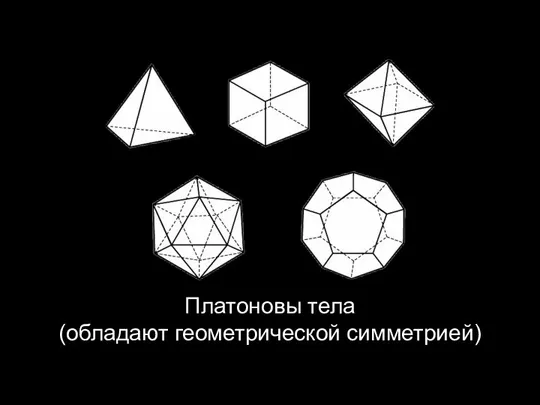
Слайд 4Платоновы тела
(обладают геометрической симметрией)
Слайд 6Симметрия - неизменность объекта при каких-либо его преобразованиях или изменениях.
Например: лист обладает

зеркальной симметрией относительно стебля
Слайд 7Что делает эти столы симметричными?

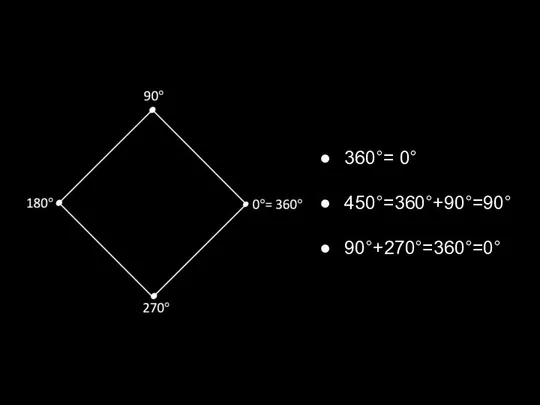
Слайд 8360°= 0°
450°=360°+90°=90°
90°+270°=360°=0°
Слайд 9Группа - множество элементов (например: симметрий какого-то объекта), причем:
Среди элементов есть особый,

называемый тождественным, который просто “ничего не делает”.
Элементы можно “компоновать” или “складывать” между собой и снова получать сходный элемент.
Для любого элемента, можно отыскать другой такой элемент, что их “сумма” этот самый особый тождественный элемент.
Слайд 10Целые числа - очень простой и всем знакомый пример группы:
0+5=5 0+100500 = 100500 0+Х

= Х Нуль - этот “особый” тождественный элемент
Для 5 есть -5 и их сумма - нуль
Для 100500 есть -100500 и их сумма - нуль
Для любого числа Х есть число -Х и их сумма - нуль!
Слайд 11Множество симметрий АБСОЛЮТНО любого объекта образует группу!

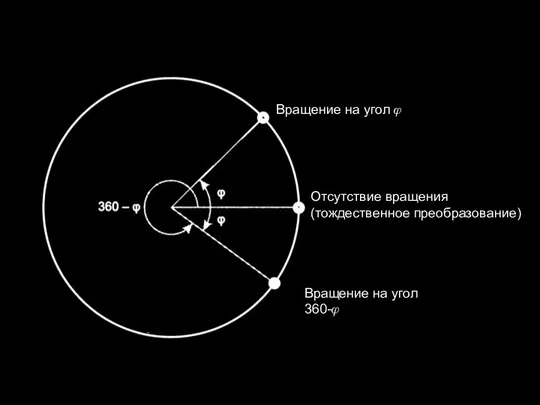
Слайд 12Вращение на угол ?
Вращение на угол 360-?
Отсутствие вращения (тождественное преобразование)
Слайд 13Штурвал при повороте переходит в себя
=

Слайд 14У настоящей бабочки есть лапки
Реальный стол - не идеальной формы

Слайд 15Зеркальная симметрия биологических видов

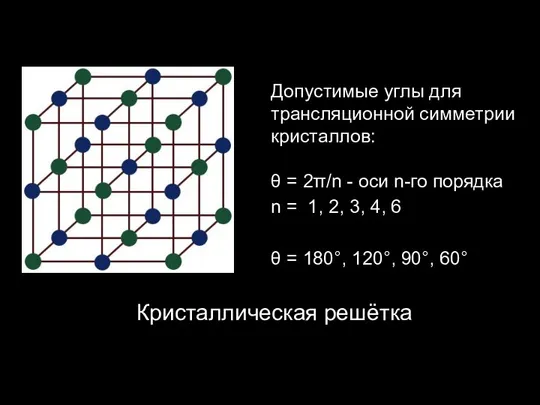
Слайд 16Кристаллическая решётка
Допустимые углы для трансляционной симметрии кристаллов:
θ = 2π/n - оси
n-го порядка
n = 1, 2, 3, 4, 6
θ = 180°, 120°, 90°, 60°
Слайд 17Трех -
Четырех -
Шести -
угольные паркеты

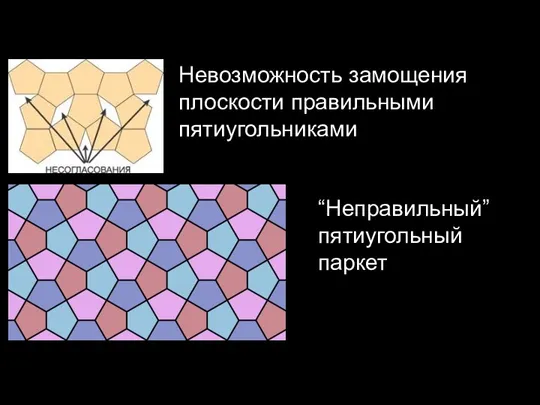
Слайд 18Невозможность замощения плоскости правильными пятиугольниками
“Неправильный” пятиугольный паркет
Слайд 19Разные типы адронов:
Протоны и нейтроны в атоме
Мезоны (переносчики сильного взаимодействия)
Диаграмма октета
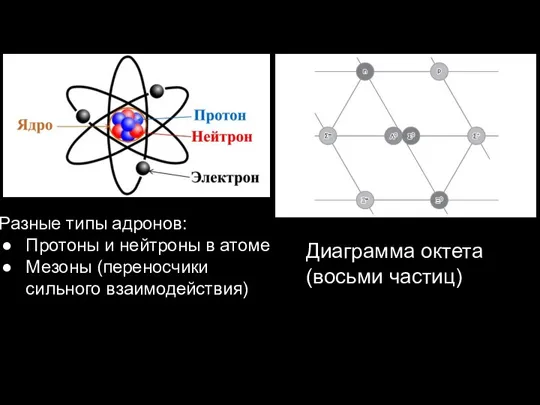
(восьми частиц)
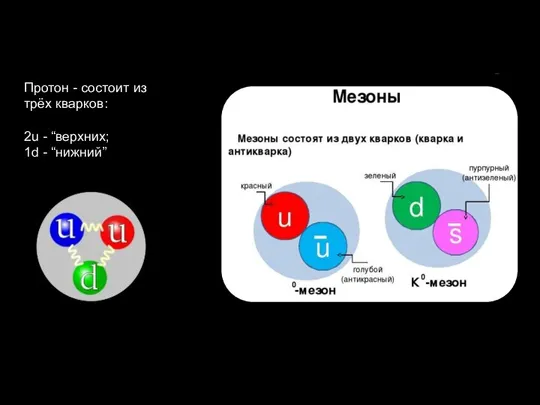
Слайд 20Протон - состоит из
трёх кварков:
2u - “верхних;
1d - “нижний”
Слайд 21Рекомендуемая литература:
Э. Френкель - “Любовь и математика”
Р. Фейнман - “Характер физических законов”
Л.Б.

Окунь - “? ? ? … Z”
П.С. Александров - “Введение в теорию групп” (выпуск 7 серии “Библиотечка квант”)
Слайд 22Присоединяйтесь к миру науки!
У нас интересно
и есть котики :3






















 Объем пирамиды
Объем пирамиды 1 урок. Аксиомы стереометрии
1 урок. Аксиомы стереометрии Как можно сравнивать размеры больших и малых тел
Как можно сравнивать размеры больших и малых тел Степень с рациональным показателем. Множество рациональных чисел
Степень с рациональным показателем. Множество рациональных чисел Обратные тригонометрические функции и их свойства
Обратные тригонометрические функции и их свойства Тренажер по логарифмам
Тренажер по логарифмам Плоскость. Уравнение плоскости по точке и нормальному вектору
Плоскость. Уравнение плоскости по точке и нормальному вектору Рациональные дроби и их свойства
Рациональные дроби и их свойства Решение СЛАУ методом Крамера
Решение СЛАУ методом Крамера Презентация на тему Математический диктант (1 класс)
Презентация на тему Математический диктант (1 класс)  Построение сечений
Построение сечений Параллелограмм. Свойства. Признаки
Параллелограмм. Свойства. Признаки Векторный анализ - теория поля. Векторное поле. Лекция 17
Векторный анализ - теория поля. Векторное поле. Лекция 17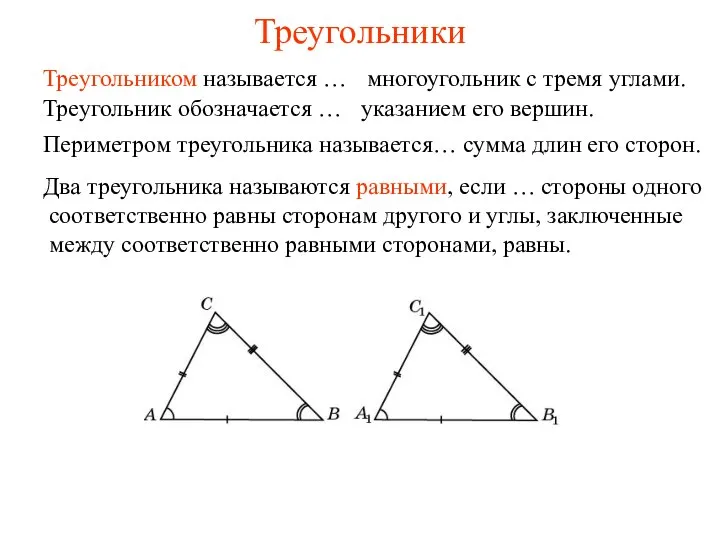 Треугольники
Треугольники 2.3. Векторная алгебра
2.3. Векторная алгебра Сумма углов геометрических фигур. Транспортир
Сумма углов геометрических фигур. Транспортир Логарифмическая линейка
Логарифмическая линейка Иррациональные уравнения
Иррациональные уравнения Функции. Область определения и множество значений; график функции; построение графиков функций, заданных различными способами
Функции. Область определения и множество значений; график функции; построение графиков функций, заданных различными способами Обобщающий урок по теме: «Степень с натуральным показателем» В 7 «В» классе Учитель Эздекова Ф.Х.
Обобщающий урок по теме: «Степень с натуральным показателем» В 7 «В» классе Учитель Эздекова Ф.Х. Умножение для ленивых? 5 класс
Умножение для ленивых? 5 класс Блиц-турнир
Блиц-турнир Матрицы. Действия над матрицами
Матрицы. Действия над матрицами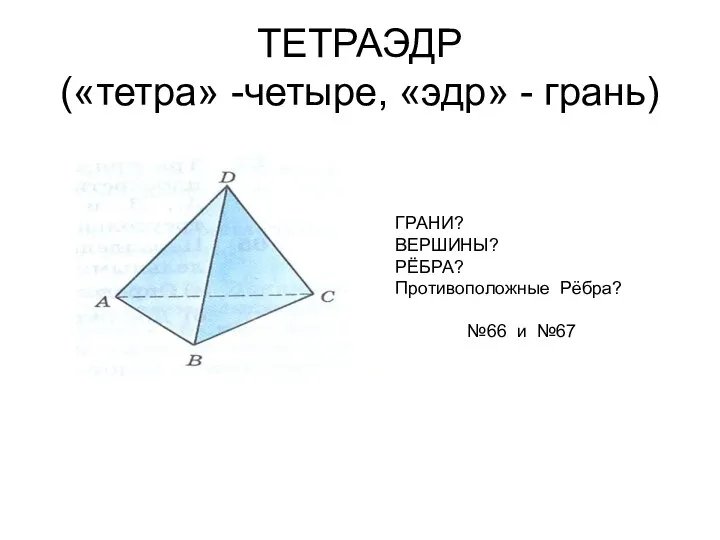 Тетраэдр (тетра -четыре, эдр - грань)
Тетраэдр (тетра -четыре, эдр - грань)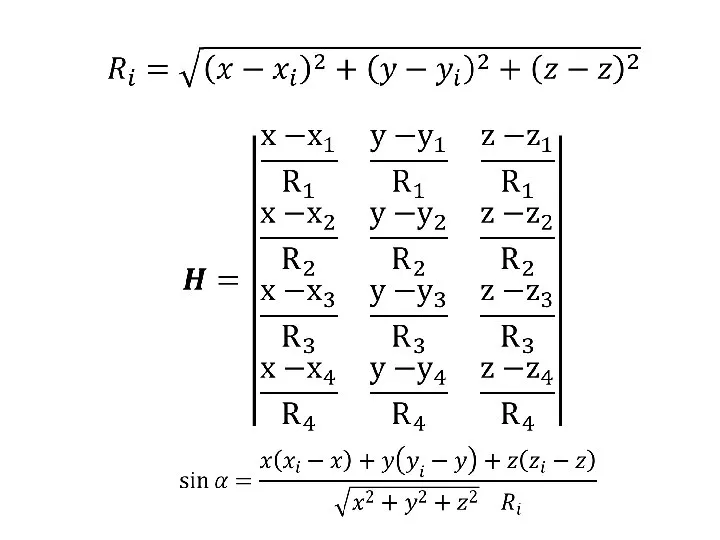 Геометрический фактор
Геометрический фактор Числовая окружность
Числовая окружность Занимательная математика
Занимательная математика Тригонометрическая и показательная форма комплексного числа
Тригонометрическая и показательная форма комплексного числа